Capítulo 9 Análises Multidimensionais
Pré-requisitos do capítulo
Pacotes e dados que serão utilizados neste capítulo.
## Pacotes
library(ade4)
library(ecodados)
library(tidyverse)
library(vegan)
library(pvclust)
library(BiodiversityR)
library(labdsv)
library(ggplot2)
library(gridExtra)
library(ape)
library(FactoMineR)
library(factoextra)
library(FD)
library(palmerpenguins)
library(GGally)
library(fields)
library(ade4)
library(ggord)
library(udunits2)
library(adespatial)
library(spdep)
library(mvabund)
library(reshape)
## Dados
sp_compos <- ecodados::bocaina
species <- ecodados::com_birds
env <- ecodados::env_birds
xy <- ecodados::birds.xy
bocaina.env <- ecodados::bocaina.env
bocaina.xy <- ecodados::bocaina.xy
anuros_permanova <- ecodados::anuros_permanova
macroinv <- ecodados::macroinv
fish_comm <- ecodados::fish_comm
data(mite)
data(doubs)
data(mite.env)
## Traduzir nomes para português
colnames(penguins) <- c("especies", "ilha", "comprimento_bico", "profundidade_bico", "comprimento_nadadeira", "massa_corporal", "sexo", "ano")9.1 Aspectos teóricos
Análises multivariadas avaliam hipóteses cuja variável resposta é definida por múltiplas variáveis ao mesmo tempo, comumente expressa na forma de uma matriz quadrada ou de distância (dissimilaridade).
Em geral, análises multivariadas têm três principais utilidades: i) reduzir a dimensionalidade dos dados e encontrar a principal direção de variação dos mesmos, ii) testar relações entre matrizes, ou ainda, iii) encontrar diferenças entre grupos. Análises multivariadas podem ser utilizadas como análises exploratórias e/ou para descrever padrões em estudos ecológicos. No entanto, mesmo quando se deseja apenas explorar o conjunto de dados para encontrar possíveis padrões, a necessidade de se ter hipóteses, ou ao menos expectativas a priori, não pode ser ignorada. Antes de entrar de cabeça nas análises multivariadas, também sugerimos fortemente o estudo de métodos de amostragem e como fazer boas perguntas (Capítulo 2).
Análises multivariadas podem ser divididas, grosseiramente, em dois tipos: agrupamento e ordenação. Análises de agrupamento, em geral, tentam agrupar objetos (observações) ou descritores em grupos de maneira que objetos do mesmo grupo sejam mais semelhantes entre si do que objetos de outros grupos (Legendre and Legendre 2012). Por exemplo, os objetos podem ser localidades como “parcelas”, “riachos” ou “florestas”, enquanto os descritores são as diferentes variáveis coletadas para esses objetos (e.g., espécies, variáveis ambientais). A análise de ordenação, por sua vez, é uma operação pela qual os objetos (ou descritores) são posicionados num espaço que contém menos dimensões que o conjunto de dados original; a posição dos objetos ou descritores em relação aos outros também pode ser usada para agrupá-los.
9.1.1 Coeficientes de associação
Assim chamados genericamente, os coeficientes de associação medem o quão parecidos objetos ou descritores são entre si. Objetos estão nas linhas da matriz, enquanto descritores estão nas colunas. Geralmente objetos são as nossas unidades amostrais, enquanto os descritores são as variáveis. Quando analisamos a relação entre objetos fazemos uma análise no modo Q, ao passo que o modo R é quando analisamos a relação entre descritores. Coeficientes de associação do modo Q são medidas de (dis)similaridade ou distância, enquanto para o modo R utilizamos covariância ou correlação. Como já tratamos neste livro sobre covariância e correlação (ver Capítulo 7), neste tópico vamos falar sobre índices de distância e similaridade. Mas qual a definição destas duas quantidades?
- Similaridade são máximas (S=1) quando dois objetos são idênticos
- Distâncias são o contrário da similaridade (D=1-S) e não têm limites superiores (dependem da unidade de medida)
Existem ao menos 26 índices de similaridade que podem ser agrupados de acordo com o tipo de dado (qualitativos ou quantitativos) ou a maneira com que lidam com duplos zeros (simétricos ou assimétricos) (Legendre and Legendre 2012). Do seu lado, as distâncias só se aplicam a dados quantitativos e têm como características serem métricas, semi-métricas ou não-métricas. Vejamos agora os principais índices de similaridade e distância de cada tipo.
9.1.2 Métricas de distância
O principal coeficiente de distância usado em ecologia é a distância euclidiana. Além disso, temos ainda Canberra (variação da Distância Euclidiana), Mahalanobis (calcula a distância entre dois pontos num espaço não ortogonal, levando em consideração a covariância entre descritores), Manhattan (variação da Distância Euclidiana), Chord (elimina diferenças entre abundância total de espécies), 𝜒2 (dá peso maior para espécies raras) e Hellinger (não dá peso para espécies raras). Essas distâncias são recomendadas nos casos em que as variáveis de estudo forem contínuas, como por exemplo, variáveis morfométricas ou descritores ambientais.
Uma característica comum de conjuntos de dados ecológicos são os vários zeros encontrados em matrizes de composição. Eles surgem porque não encontramos nenhum indivíduo de uma determinada espécie num local, seja porque aquele local não tem as condições ambientais adequadas a ela, falha na detectabilidade, ou dinâmicas demográficas estocásticas de colonização-extinção (Blasco‐Moreno et al. 2019). Logo, quando dois locais compartilham ausência de espécies, não é possível atribuir uma única razão da dupla ausência. Como essas medidas de distância apresentadas acima assumem que os dados são quantitativos e não de contagem, elas não são adequadas para lidar com dados de abundância ou incidência de espécies, porque atribuem um grau de parecença a pares de locais que compartilham zeros (Legendre and Legendre 2012). Por esse motivo, precisamos de coeficientes que desconsiderem os duplos zeros. Eles são chamados de assimétricos.
Coeficientes assimétricos binários para objetos
Esses coeficientes (ou índices) são apropriados para dados de incidência de espécies (presença-ausência) e desconsideram as duplas ausências. Os índices deste tipo mais comuns utilizados em ecologia são Jaccard, Sørensen e Ochiai.
O coeficiente de Jaccard é dado por:
\[\beta_j = a/(a+b+c)\] onde
- a = número de espécies compartilhadas
- b = número de espécies exclusivas da comunidade 1
- c = número de espécies exclusivas da comunidade 2
A diferença entre os índices de Jaccard e Sørensen é que o índice de Sørensen dá peso dobrado para duplas presenças. Por conta dessas características, estes índices são adequados para quantificar diversidade beta (M. J. Anderson et al. 2011; Legendre and De Cáceres 2013). Esses índices variam entre 0 (nenhuma espécie é compartilhada entre o par de locais) a 1 (todas as espécies são compartilhadas entre o par de locais).
O coeficiente de Sørensen é dado por:
\[\beta_s = 2a/(2a+b+c)\] onde
- a = número de espécies compartilhadas
- b = número de espécies exclusivas da comunidade 1
- c = número de espécies exclusivas da comunidade 2
Coeficientes binários para descritores (R mode)
Se o objetivo for calcular a similaridade entre descritores binários (e.g., presença ou ausência de características ambientais) de pares de locais, geralmente o coeficiente recomendado é o de Sokal & Michener. Este índice está implementado na função dist.binary() do pacote ade4.
Coeficientes quantitativos para objetos
Estes são os coeficientes utilizados para dados de contagem (e.g., abundância) e quantitativos (e.g., frequência, biomassa, porcentagem de cobertura). Diferentemente das distâncias, estes coeficientes são assimétricos, ou seja, não consideram duplas ausências e, portanto, são adequados para analisar dados de composição de espécies. Além disso, uma outra característica deles é serem semi-métricos. Os índices mais comuns deste tipo são Bray-Curtis (conhecido como percentage difference, em inglês), Chord, log-Chord, Hellinger, chi-quadrado e Morisita-Horn.
Todos os índices discutidos até aqui estão implementados nas funções ade4::dist.ktab(), adespatial::dist.ldc() e vegan::vegdist().
Coeficientes para descritores (R mode) que incluem mistura de tipos de dados
É comum em análises de diversidade funcional que tenhamos um conjunto de atributos (traits) de espécies que são formados por vários tipos de dados: quantitativos (e.g., tamanho de corpo), binários (presença/ausência de uma dada característica), fuzzy (um atributo multiestado codificado em várias colunas), ordinais e circulares (e.g., distribuição de uma fenofase ao longo de um ano). O índice que lida com todos esses dados é o Gower. A versão estendida do índice de Gower pode ser encontrada na função ade4::dist.ktab().
O capítulo 7 de Legendre & Legendre (2012) fornece uma chave dicotômica para escolha do índice mais adequado.
Padronizações e transformações
É comum coletarmos múltiplas variáveis ambientais cujas unidades sejam diferentes. Por exemplo, temperatura (ºC), distância da margem (m), área (m2), etc. Para diminuir a taxa de Erro do Tipo I das análises (rejeitar a hipótese nula quando ela é verdadeira), é recomendado que padronizemos os dados utilizando distribuição Z, assim todas as variáveis passam a ter média 0 e desvio padrão 1. Essa operação garante que todas as variáveis tenham o mesmo peso nas análises que avaliam o padrão dos objetos considerando os múltiplos descritores. Essa padronização pode ser implementada na função vegan::decostand().
Outro problema comum de matrizes de dados de composição de espécies é o alto número de zeros, enquanto outras espécies podem ter altas abundâncias. Isso gera problemas em ordenações. Para diminuir essa discrepância, podemos transformar os dados, por exemplo, utilizando a distância de Hellinger ou Chord. Para dados contínuos pode ser que transformação log ou raiz quadrada ajude quando há valores muito discrepantes (leverages) que podem influenciar em demasiado a relação entre objetos ou descritores. Isso pode ser feito na função vegan::decostand().
9.2 Análises de agrupamento
O objetivo da análise de agrupamento é agrupar objetos admitindo que haja um grau de similaridade entre eles. Esta análise pode ser utilizada ainda para classificar uma população em grupos homogêneos de acordo com uma característica de interesse. A grosso modo, uma análise de agrupamento tenta resumir uma grande quantidade de dados e apresentá-la de maneira fácil de visualizar e entender (em geral, na forma de um dendrograma). No entanto, os resultados da análise podem não refletir necessariamente toda a informação originalmente contida na matriz de dados. Para avaliar o quão bem uma análise de agrupamento representa os dados originais existe uma métrica — o coeficiente de correlação cofenético — o qual discutiremos em detalhes mais adiante.
Antes de considerar algum método de agrupamento, pense porque você esperaria que houvesse uma descontinuidade nos dados; ou ainda, considere se existe algum ganho prático em dividir uma nuvem de objetos contínuos em grupos. O padrão apresentado pelo dendrograma depende do protocolo utilizado (método de agrupamento e índice de dissimilaridade); os grupos formados dependem do nível de corte escolhido.
A matriz deve conter os objetos a serem agrupados (e.g., espécies) nas linhas e as variáveis (e.g., locais de coleta ou medidas morfológicas) nas colunas. A escolha do método de agrupamento é crítica para a escolha de um coeficiente de associação. É importante compreender as propriedades dos métodos de agrupamento para interpretar corretamente a estrutura ecológica que eles evidenciam (Legendre and Legendre 2012). De acordo com a classificação de Sneath & Sokal (1973), existem cinco tipos de métodos: i) sequenciais ou simultâneos, ii) aglomerativo ou divisivo, iii) monotéticos ou politéticos, iv) hierárquico ou não hierárquicos e v) probabilístico. Sugerimos a leitura do livro citado anteriormente para aprofundar seus conhecimentos sobre os diferentes métodos.
9.2.1 Agrupamento hierárquico
Métodos hierárquicos podem ser divididos naqueles que consideram o centroide ou a média aritmética entre os grupos. O principal método hierárquico que utiliza a média aritmética é o UPGMA (Agrupamento pelas médias aritméticas não ponderadas), e o principal método que utiliza centroides é a Distância mínima de Ward.
O UPGMA funciona da seguinte forma: a maior similaridade (ou menor distância) identifica os próximos agrupamentos a serem formados. Após esse evento, o método calcula a média aritmética das similaridades ou distâncias entre um objeto e cada um dos membros do grupo ou, no caso de um grupo previamente formado, entre todos os membros dos dois grupos. Todos os objetos recebem pesos iguais no cálculo.
O método de Ward é baseado no critério de quadrados mínimos (OLS), o mesmo utilizado para ajustar um modelo linear (Capítulo 7). O objetivo é definir os grupos de maneira que a soma de quadrados (i.e. similar ao erro quadrado da ANOVA) dentro dos grupos seja minimizada (Borcard, Gillet, and Legendre 2018).
No entanto, para interpretar os resultados precisamos antes definir um nível de corte, que vai nos dizer quantos grupos existem. Há vários métodos para definir grupos, desde os heurísticos aos que utilizam reamostragem (bootstrap). Se quisermos interpretar este dendrograma, podemos, por exemplo, estabelecer um nível de corte de 50% de distância (ou seja, grupos cujos objetos tenham ao menos 50% de similaridade entre si).
Checklist
Verifique se não há espaço nos nomes das colunas e linhas
Se os dados forem de abundância, recomenda-se realizar a transformação de Hellinger (Legendre and Gallagher 2001). Esta transformação é necessária porque a matriz de comunidades (em especial, com a presença de muitas espécies raras) pode causar distorções nos métodos de ordenação baseados em distância Euclidiana (Legendre and Gallagher 2001)
Se a matriz original contiver muitos valores discrepantes (e.g., uma espécie muito mais ou muito menos abundante que outras) é necessário transformar os dados usando
log1p(). No entanto, deve-se fazer ou a transformação de Hellinger ou logarítmica e nunca as duas ao mesmo tempoSe as variáveis forem medidas tomadas em diferentes escalas (metros, graus celsius etc.), é necessário padronizar cada variável para ter a média 0 e desvio padrão 1. Isso pode ser feito utilizando a função
decostand()do pacotevegan
Exemplo 1
Neste exemplo, vamos utilizar um conjunto de dados que contém girinos de espécies de anuros coletados em 14 poças com diferentes coberturas de dossel (Provete et al. 2014).
Pergunta
- Existem grupos de espécies de anfíbios anuros com padrões de ocorrência similar ao longo das poças?
Predições
- Iremos encontrar ao menos dois grupos de espécies: aquelas que ocorrem em poças dentro de floresta (i.e., maior cobertura de dossel) versus aquelas que ocorrem em poças de áreas abertas (menor cobertura de dossel)
Variáveis
- Variáveis preditoras: a matriz de dados contém a abundância das espécies nas linhas e locais (poças) nas colunas
Análises
Para começar, vamos primeiro importar os dados e depois calcular a matriz de distância que seja adequada para o tipo de dado que temos (abundância de espécies - dados de contagem) (Figura 9.1).
## Composição de espécies (seis primeiras localidades)
head(sp_compos)
#> BP4 PP4 PP3 AP1 AP2 PP1 PP2 BP9 PT1 PT2 PT3 BP2 PT5
#> Aper 0 3 0 0 2 0 0 0 0 0 0 181 0
#> Bahe 859 14 14 0 87 312 624 641 0 0 0 14 0
#> Rict 1772 1517 207 573 796 0 0 0 0 0 0 0 0
#> Cleuco 0 0 0 0 0 0 0 0 0 29 369 0 84
#> Dmic 0 0 6 60 4 0 0 0 2758 319 25 0 329
#> Dmin 0 84 344 1045 90 0 0 0 8 0 0 0 0
## Matriz de similaridade com o coeficiente de Morisita-Horn
distBocaina <- vegdist(x = sp_compos, method = "horn")
## Agrupamento com a função hclust e o método UPGMA
dendro <- hclust(d = distBocaina, method = "average")
## Visualizar os resultados
plot(dendro, main = "Dendrograma",
ylab = "Similaridade (índice de Horn)",
xlab="", sub="")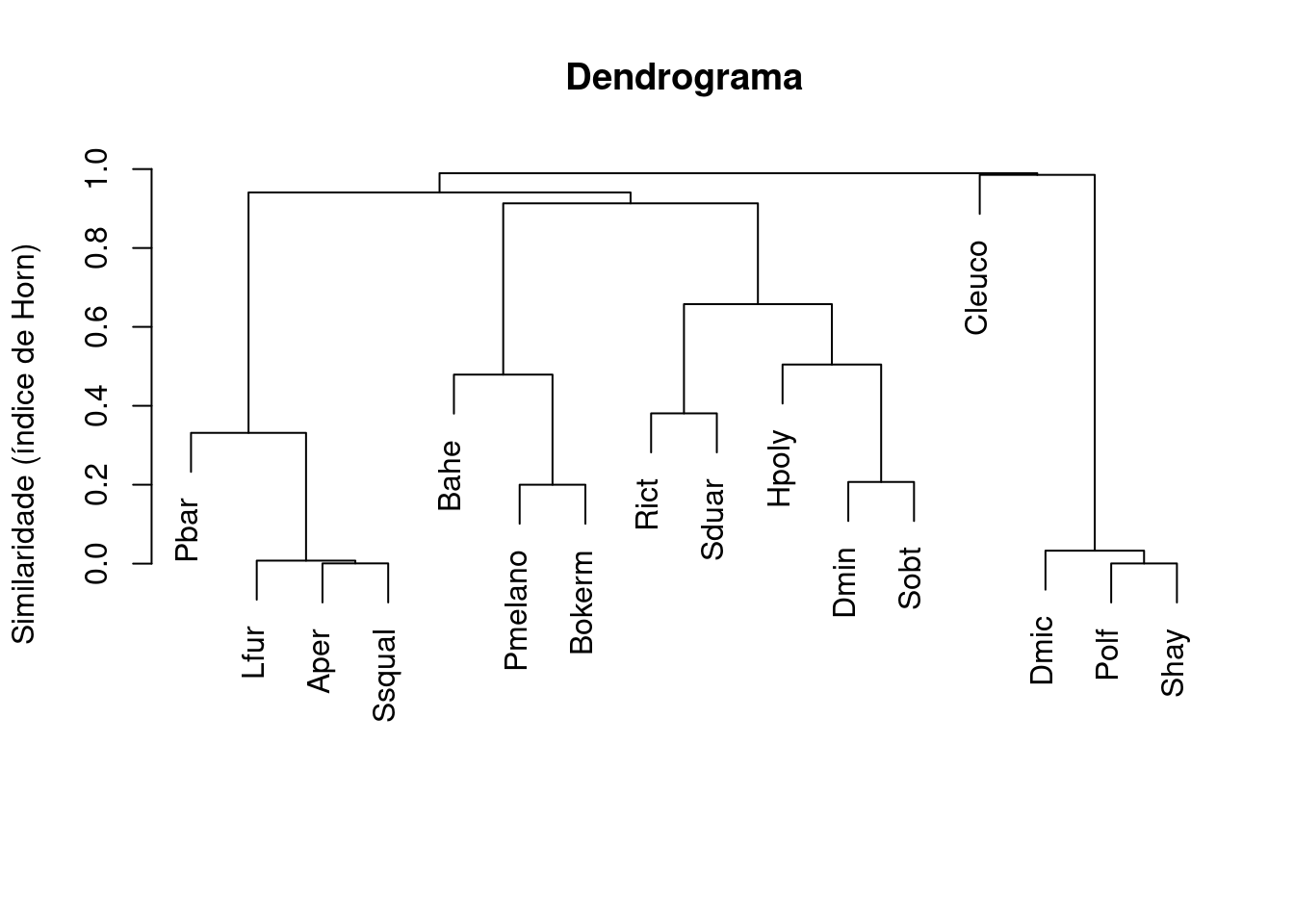
Figura 9.1: Dendrograma mostrando uma análise de agrupamento de anuros.
Avaliando a qualidade do dendrograma
Precisamos verificar se o agrupamento reduziu a dimensionalidade da matriz de forma eficiente, de maneira a não distorcer a informação. Fazemos isso calculando o Coeficiente de Correlação Cofenética que é uma medida que nos indica quão bem o resultado do agrupamento corresponde às (dis)similaridades originais.
## Coeficiente de correlação cofenética
cofresult <- cophenetic(dendro)
cor(cofresult, distBocaina)
#> [1] 0.9455221Um coeficiente de correlação cofenética > .7 indica uma boa representação. Portanto, o nosso resultado de 0.9455221 é alto, garantindo que o dendrograma é adequado (Figura 9.2). Note que testar a “significância” deste coeficiente não é adequado, já que seria algo tautológico (circular). Claro que definir o que seria um valor “alto” ou “baixo” da correlação é um pouco arbitrário, mas pode-se usar como “regra do polegar”.
## Gráfico
plot(dendro, main = "Dendrograma",
ylab = "Similaridade (índice de Horn)",
xlab="", sub="")
k <- 4
n <- ncol(sp_compos)
MidPoint <- (dendro$height[n-k] + dendro$height[n-k+1]) / 2
abline(h = MidPoint, lty=2)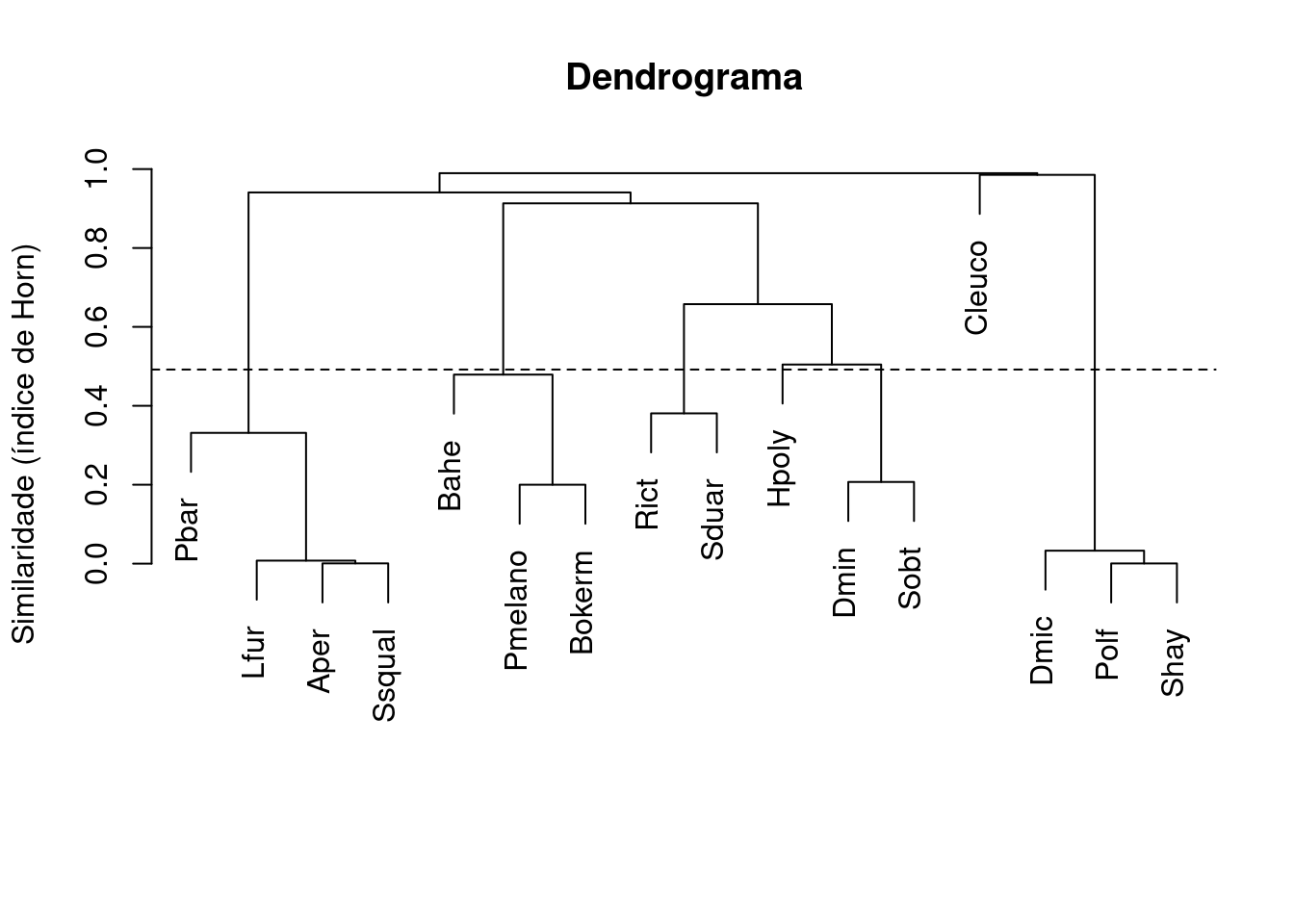
Figura 9.2: Dendrograma mostrando uma análise de agrupamento de anuros com uma linha de corte formando cinco grupos.
Nesse caso teremos a formação de cinco grupos, representados pelos nós que estão abaixo da linha de corte. Portanto, o resultado não suporta a nossa hipótese a priori que predizia a formação de apenas dois grupos de espécies.
Exemplo 2
No exemplo anterior, vimos que é difícil interpretar os grupos baseado num nível de corte. A seguir, vamos utilizar o pacote pvclust que calcula automaticamente o nível de corte de similaridade baseado no Bootstrap de cada nó. Uma desvantagem deste método é que ele somente aceita índices de similaridade da função dist(), que possui apenas a distância Euclidiana, Manhattan e Canberra. Uma maneira de contornarmos essa limitação é utilizar transformações dos dados disponíveis na função disttransform() no pacote BiodiversityR ou a função decostand() do pacote vegan. Também é possível utilizar a transformação de Box-Cox para dados multivariados, disponível no material suplementar de Legendre & Borcard (2018). Esta transformação é geralmente utilizada para tornar a distribuição dos dados mais simétrica (menos enviesada para valores extremos: reduzir o skewness dos dados).
Análises
Vamos utilizar o mesmo conjunto de dados do Exemplo 1 para responder à mesma pergunta. Aqui vamos utilizar a distância de Chord (que é indicada para dados de composição de espécies) para calcular a matriz de distância. Se transformarmos uma matriz usando a transformação Chord e depois calcularmos a distância Euclidiana, isso equivale à calcular diretamente a distância de Chord (Figura 9.3).
## Dados
head(t(sp_compos))
#> Aper Bahe Rict Cleuco Dmic Dmin Hpoly Lfur Pbar Polf Pmelano Sduar Shay Sobt Ssqual Bokerm
#> BP4 0 859 1772 0 0 0 61 3 387 0 0 0 0 0 0 0
#> PP4 3 14 1517 0 0 84 275 0 187 0 0 1150 6 0 0 1
#> PP3 0 14 207 0 6 344 388 0 0 0 0 428 0 0 0 0
#> AP1 0 0 573 0 60 1045 1054 0 0 0 0 476 92 13 0 0
#> AP2 2 87 796 0 4 90 3002 0 0 2 0 7 0 5 0 0
#> PP1 0 312 0 0 0 0 329 0 0 0 0 0 0 0 0 0
## Passo 1: transformar para distância de Chord
bocaina_transf <- disttransform(t(sp_compos), "chord")
## Passo 2: realizar pvclust com método average e distância euclidiana
analise <- pvclust(bocaina_transf, method.hclust = "average", method.dist = "euclidean", quiet = TRUE)
## Passo 3: dendrograma
plot(analise, hang=-1, main = "Dendrograma com valores de P",
ylab = "Distância Euclideana",
xlab="", sub="")
pvrect(analise)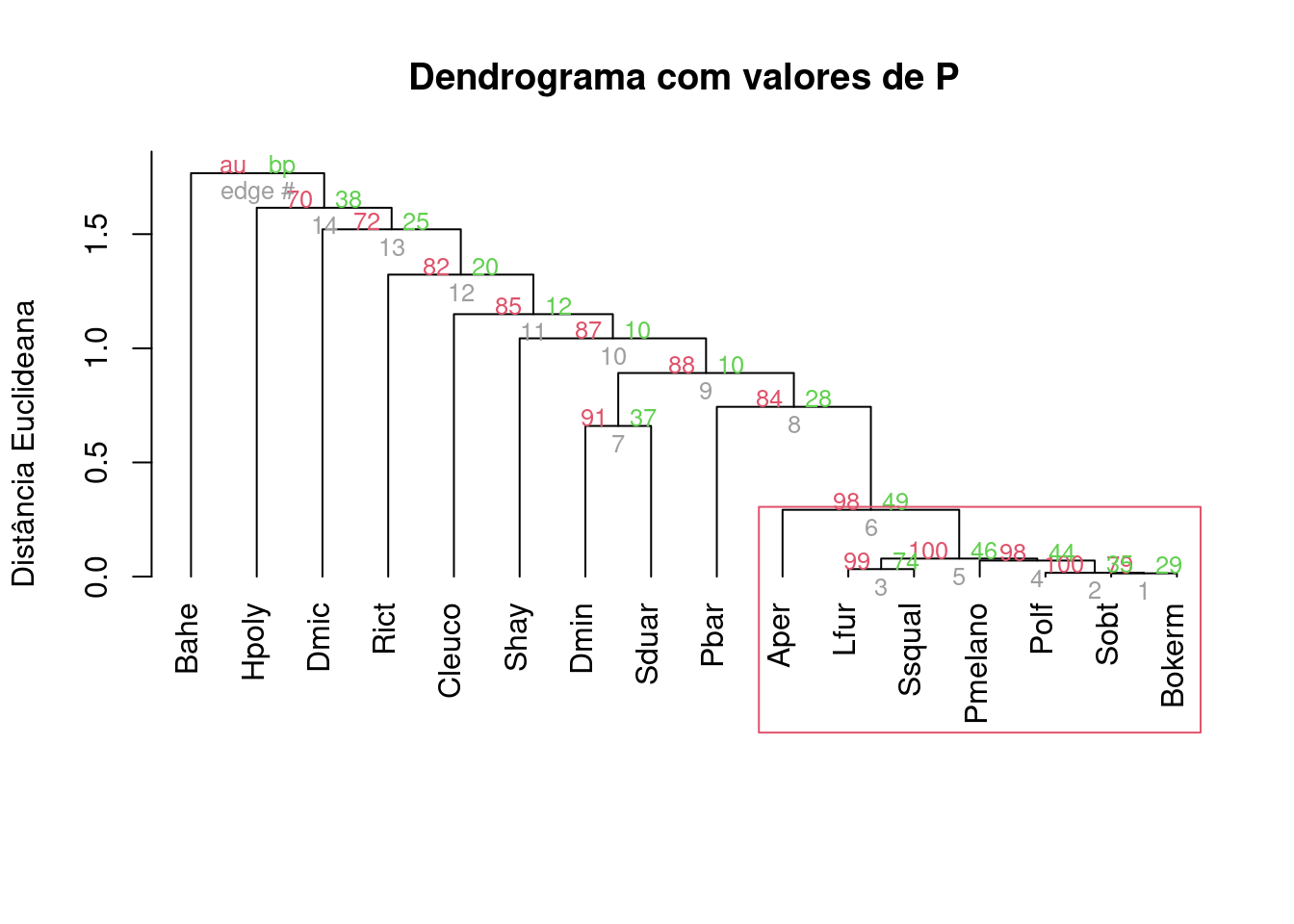
Figura 9.3: Dendrograma mostrando uma análise de agrupamento de anuros com uma linha de corte criada por bootstrap e usando distância de Chord.
É possível notar que existe um único grupo com BS > 95%. Agora vamos tentar usar a distância de Hellinger, que é recomendada (junto com a distância de Chord) para transformar dados de composição de espécies (Legendre and Gallagher 2001) (Figura 9.4).
## Passo 1: transformar dados com Hellinger
bocaina_transf2 <- disttransform(t(bocaina), "hellinger")
## Passo 2: realizar pvclust com método average e distância euclidiana
analise2 <- pvclust(bocaina_transf2, method.hclust="average", method.dist="euclidean", quiet = TRUE)
## Passo 3: dendrograma
plot(analise2, hang=-1, main = "Dendrograma com valores de P",
ylab = "Distância Euclideana",
xlab="", sub="")
k <- 4
n <- ncol(sp_compos)
MidPoint <- (dendro$height[n-k] + dendro$height[n-k+1]) / 2
abline(h = MidPoint, lty=2)
pvrect(analise2)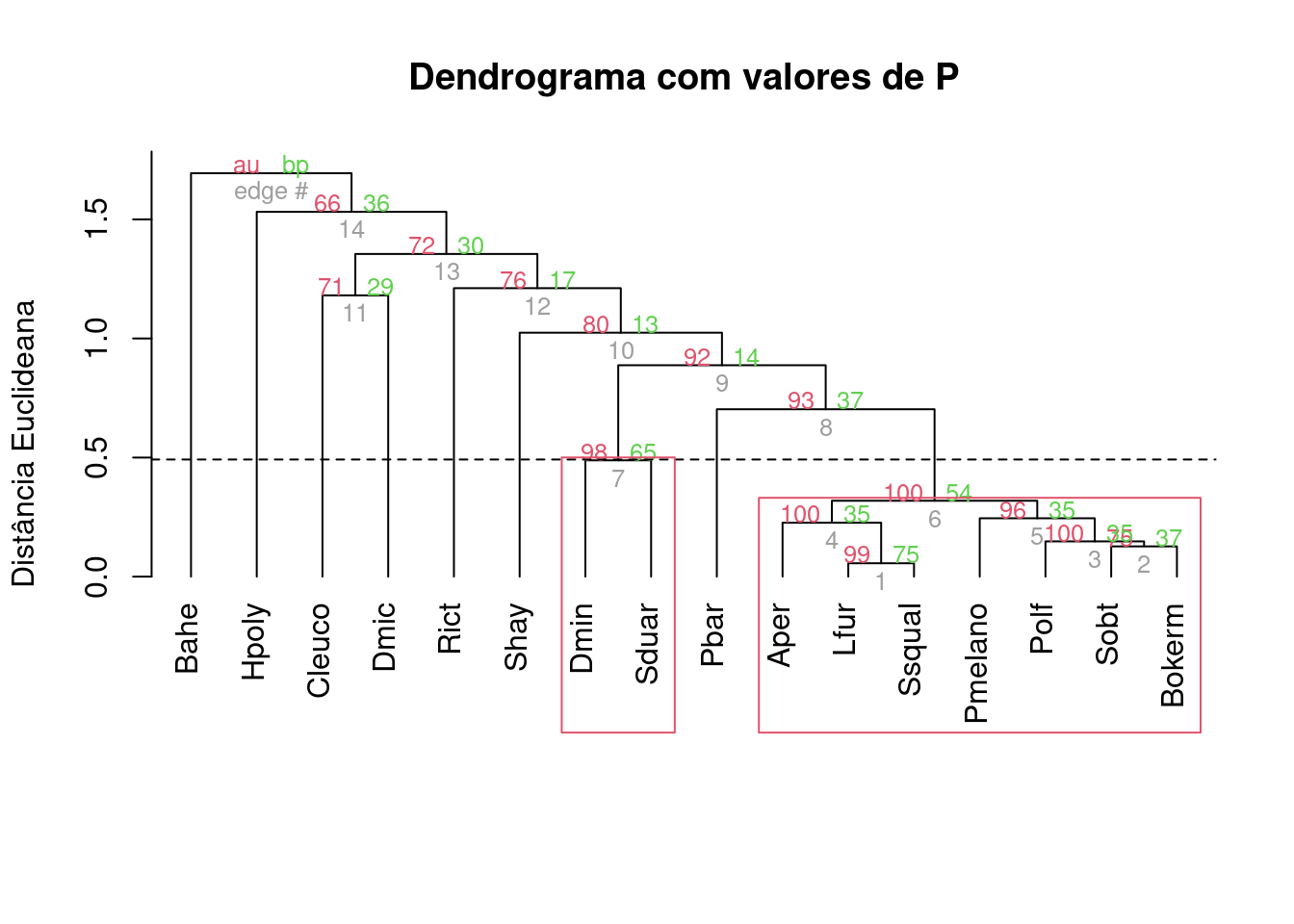
Figura 9.4: Dendrograma mostrando uma análise de agrupamento de anuros com uma linha de corte criada por bootstrap e usando distância de Hellinger.
Interpretação dos resultados
Notem que se mudarmos o coeficiente de associação, o resultado também muda. Agora temos um grupo a mais, composto por Dendropsophus minutus e Scinax duartei que não apareciam antes. Isso se deve ao fato de que a distância de Hellinger dá menos peso para espécies raras do que a Chord.
Neste sentido, os dados não suportam a nossa hipótese inicial da formação de dois grupos, independentemente do coeficiente de associação utilizado e do cálculo automático do nível de corte baseado na reamostragem.
9.2.2 Agrupamento não-hierárquico (K-means)
Ao contrário do dendrograma, o K-means é um agrupamento não-hierárquico e, desse modo, não é otimizado para buscar grupos menores aninhados em grupos maiores. Resumidamente, podemos calcular o K-means a partir de uma matriz quadrada ou de distância. Essa técnica procura particionar os objetos em k grupos de maneira a minimizar a soma de quadrados entre grupos e maximizá-la dentro dos grupos. Um critério similar ao de uma ANOVA (Capítulo 7). Um diferencial do K-means em relação aos agrupamentos hierárquicos é que o usuário pode escolher antecipadamente o número de grupos que deseja formar.
Exemplo 1
Para este exemplo, iremos utilizar um conjunto de dados disponível no pacote ade4 que contém dados de 27 espécies de peixes coletados em 30 pontos ao longo do Rio Doubs, na fronteira entre a França e Suíça.
Pergunta
- Qual é o número de grupos que melhor sumariza o padrão de ocorrência de espécies de peixes ao longo de um riacho?
📝 Importante
Neste caso, estamos realizando uma análise exploratória e não temos uma predição.
Variáveis
- Variáveis resposta: composição de espécies de peixes
Checklist
- Vamos normalizar os dados de abundância antes de entrar na análise propriamente, já que existem muitos zeros na matriz
Análises
Vamos iniciar selecionando e padronizando os dados.
## Mostrar somente seis primeiras espécies de seis localidades
head(doubs$fish)[,1:6]
#> Cogo Satr Phph Neba Thth Teso
#> 1 0 3 0 0 0 0
#> 2 0 5 4 3 0 0
#> 3 0 5 5 5 0 0
#> 4 0 4 5 5 0 0
#> 5 0 2 3 2 0 0
#> 6 0 3 4 5 0 0
## Verificar se existem localidades sem nenhuma ocorrência
rowSums(doubs$fish)
#> 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
#> 3 12 16 21 34 21 16 0 14 14 11 18 19 28 33 40 44 42 46 56 62 72 4 15 11 43 63 70 87 89
## Retirar a linha 8 (rio sem nenhuma ocorrência de peixe)
spe <- doubs$fish[-8,]
## Função do pacote vegan para normalizar os dados
spe.norm <- decostand(x = spe, method = "normalize") O argumento centers na função kmeans() indica o número de grupos que se quer formar. Neste exemplo, estamos utilizando centers = 4.
## K-Means
spe.kmeans <- kmeans(x = spe.norm, centers = 4, nstart = 100)
spe.kmeans
#> K-means clustering with 4 clusters of sizes 8, 12, 6, 3
#>
#> Cluster means:
#> Cogo Satr Phph Neba Thth Teso Chna Chto Lele Lece Baba Spbi Gogo
#> 1 0.00000000 0.006691097 0.02506109 0.06987391 0.006691097 0.006691097 0.10687104 0.09377516 0.14194394 0.2011411 0.24327992 0.1326062 0.28386032
#> 2 0.10380209 0.542300691 0.50086515 0.43325916 0.114024105 0.075651573 0.00000000 0.00000000 0.06983991 0.1237394 0.02385019 0.0000000 0.05670453
#> 3 0.06167791 0.122088022 0.26993915 0.35942538 0.032664966 0.135403325 0.06212775 0.21568957 0.25887226 0.2722562 0.15647062 0.1574388 0.16822286
#> 4 0.00000000 0.000000000 0.00000000 0.00000000 0.000000000 0.000000000 0.05205792 0.00000000 0.07647191 0.3166705 0.00000000 0.0000000 0.20500174
#> Eslu Pefl Rham Legi Scer Cyca Titi Abbr Icme Acce Ruru Blbj Alal
#> 1 0.20630360 0.16920496 0.2214275 0.19066542 0.13171275 0.16019126 0.26230024 0.19561641 0.1331835 0.26713081 0.32103755 0.22883055 0.3326939
#> 2 0.04722294 0.02949244 0.0000000 0.00000000 0.00000000 0.00000000 0.03833408 0.00000000 0.0000000 0.00000000 0.01049901 0.00000000 0.0000000
#> 3 0.12276089 0.17261621 0.0793181 0.06190283 0.04516042 0.06190283 0.14539027 0.01473139 0.0000000 0.03192175 0.32201597 0.01473139 0.1095241
#> 4 0.07647191 0.00000000 0.0000000 0.05205792 0.07647191 0.00000000 0.00000000 0.00000000 0.0000000 0.18058775 0.31667052 0.05205792 0.7618709
#> Anan
#> 1 0.18873077
#> 2 0.00000000
#> 3 0.04739636
#> 4 0.00000000
#>
#> Clustering vector:
#> 1 2 3 4 5 6 7 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
#> 2 2 2 2 3 2 2 3 2 2 2 2 2 2 3 3 3 3 1 1 1 4 4 4 1 1 1 1 1
#>
#> Within cluster sum of squares by cluster:
#> [1] 0.4696535 2.5101386 1.7361453 0.3560423
#> (between_SS / total_SS = 66.7 %)
#>
#> Available components:
#>
#> [1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss" "size" "iter" "ifault"O objeto que fornece o resultado contém: i) o tamanho (número de objetos) em cada um dos 4 grupos, ii) o centroide de cada grupo e o pertencimento de cada espécie a cada grupo, e iii) o quanto da Soma de Quadrados dos dados é explicada por esta conformação de grupos.
No entanto, não é possível saber a priori qual o número “ideal” de grupos. Para descobrir isso, repetimos o k-means com uma série de valores de K. Isso pode ser feito na função cascadeKM().
## Repetindo o K-Means
spe.KM.cascade <- cascadeKM(spe.norm, inf.gr = 2, sup.gr = 10, iter = 100, criterion = "ssi") Tanto calinski quando ssi são bons critérios para encontrar o número ideal de grupos. Quanto maior o valor de ssi, melhor (veja ?cascadeKM() mais detalhes). Os valores de ssi é o critério utilizado pelo algoritimo para achar o agrupamento ótimo dos objetos (Figura 9.5).
## Resumo dos resultados
spe.KM.cascade$results
#> 2 groups 3 groups 4 groups 5 groups 6 groups 7 groups 8 groups 9 groups 10 groups
#> SSE 8.2149405 6.4768108 5.0719796 4.3015573 3.58561200 2.9523667 2.4840549 2.0521888 1.7599292
#> ssi 0.1312111 0.1685126 0.1409061 0.1299662 0.08693436 0.1481826 0.1267918 0.1134307 0.1226392
## Gráfico
plot(spe.KM.cascade, sortg = TRUE)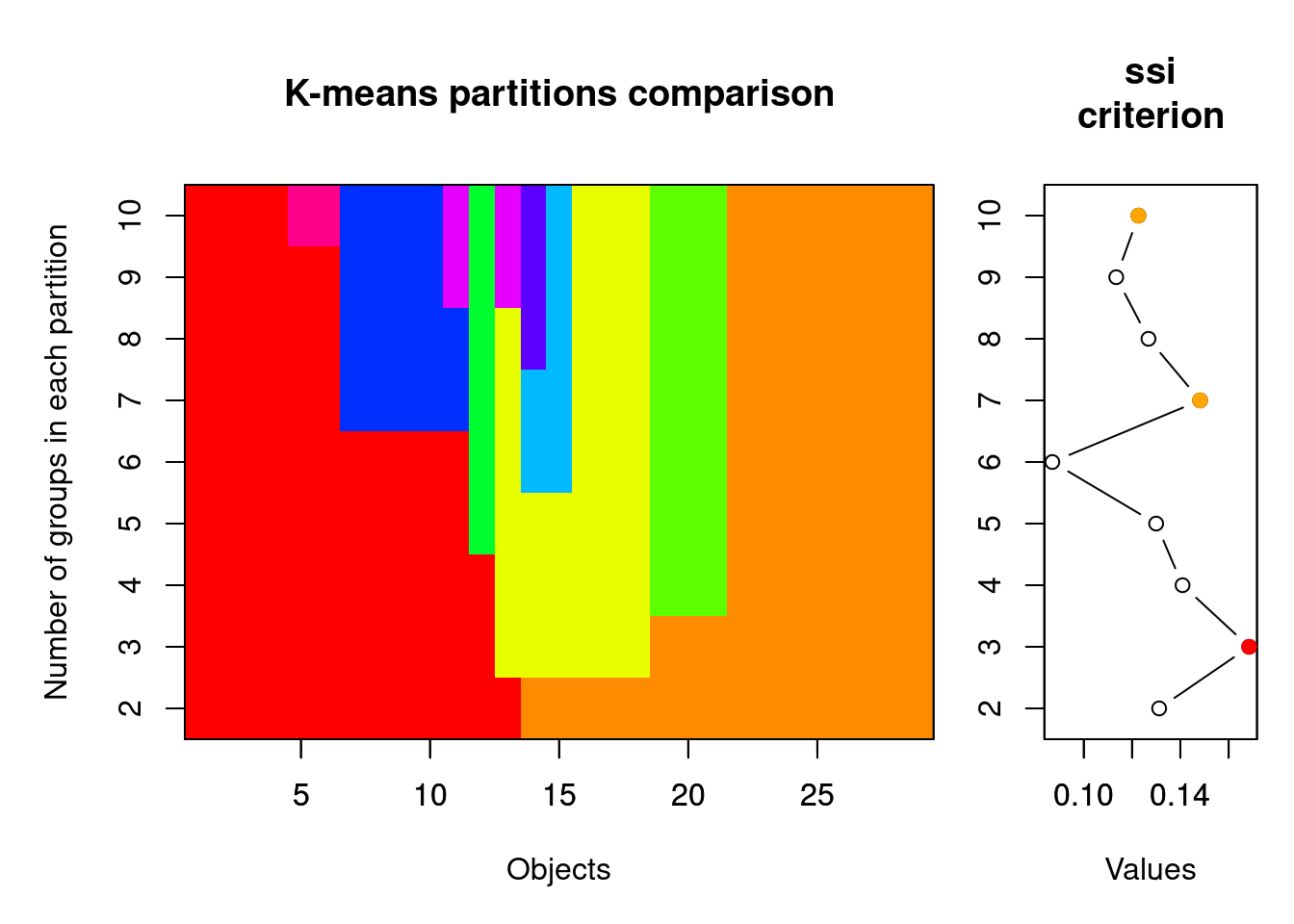
Figura 9.5: Gráficos mostrando os resultados da análise de K-Means.
Interpretação dos resultados
Diferentemente da nossa predição inicial, o resultado da análise mostra que o número ideal de grupos para explicar a variância no padrão de ocorrência de espécies é 3. Notem que o SSI máximo é alcançado neste número de grupos 0.1685126 (também indicado pela bola vermelha no plot).
9.2.3 Espécies indicadoras
Uma pergunta normalmente feita por ecólogos é: qual espécie pode ser indicadora de uma determinada condição ambiental (e.g., poluição)?
O índice IndVal mede dois aspectos das espécies: fidelidade e especificidade. Uma alta fidelidade significa que espécies ocorrem em todos os locais do grupo, e uma alta especificidade significa que as espécies ocorrem somente naquele grupo. Uma boa espécie indicadora é aquela na qual todos os indivíduos ocorrem em todas as amostras referentes a um grupo específico. A especificidade é dada pela divisão da abundância média da espécie no grupo pela somatória das abundâncias médias dos grupos. Fidelidade é igual ao número de lugares no grupo onde a espécie está presente dividido pelo número total de lugares do grupo (Dufrêne and Legendre 1997).
Espécies raras podem receber o mesmo valor de IndVal das espécies indicadoras, porém são chamadas de indicadoras assimétricas, uma vez que contribuem com a especificidade do habitat, mas não servem para predizer grupos. Ao contrário, as espécies indicadoras são verdadeiros indicadores simétricos e podem ser usadas para predizer grupos.
A análise procede da seguinte forma:
Uma matriz de distância é construída e as unidades amostrais são classificadas com alguma análise de agrupamento, hierárquico ou não
A variável ambiental para a qual se deseja classificar os grupos é inserida
As espécies indicadoras de cada grupo são formadas através do cálculo da especificidade e fidelidade, obtendo-se o valor de IndVal para cada espécie
Por fim, o conjunto de dados originais é comparado para ver se a análise faz sentido
O cálculo da significância do índice de IndVal é feito por aleatorização de Monte Carlo. Os métodos de Monte Carlo utilizam números aleatórios de dados reais para simular certos padrões esperados na ausência de um processo ecológico específico (Legendre and Legendre 2012). Assim, o valor do índice é aleatorizado 999 vezes (ou o número de vezes que você optar) dentro dos tratamentos e o valor de P é dado pelo número de vezes em que o índice observado foi igual ou maior que os valores aleatorizados. Portanto, o IndVal fornece um conjunto de espécies que são indicadoras de um grupo de locais (e.g., muito poluídos), que por sua vez precisam ser definidos utilizando alguma técnica de agrupamento, como as que vimos anteriormente.
Exemplo 1
Para este exemplo, vamos usar o mesmo conjunto de dados utilizado acima com abundância de 16 espécies de girinos coletados em 14 poças com diferentes graus de cobertura de dossel na Serra da Bocaina (Provete et al. 2014).
Pergunta
- Podemos utilizar as espécies de girinos como indicadoras da fitofisionomia?
Predições
- Espécies terrestres serão indicadoras de área aberta, enquanto espécies arborícolas serão indicadoras de áreas florestais
Variáveis
- Variáveis resposta: mesma matriz já utilizada contendo a abundância de girinos ao longo de poças na Serra da Bocaina
Análises
O IndVal está disponível tanto no pacote indicspecies, quando no labdsv. Para este exemplo, iremos usar o labdsv. Primeiro, vamos agrupar as unidades amostrais (poças) que informa os grupos de fitofisionomias onde as poças se localizam e para os quais deseja-se encontrar espécies indicadoras.
## Dados
head(bocaina)
#> BP4 PP4 PP3 AP1 AP2 PP1 PP2 BP9 PT1 PT2 PT3 BP2 PT5
#> Aper 0 3 0 0 2 0 0 0 0 0 0 181 0
#> Bahe 859 14 14 0 87 312 624 641 0 0 0 14 0
#> Rict 1772 1517 207 573 796 0 0 0 0 0 0 0 0
#> Cleuco 0 0 0 0 0 0 0 0 0 29 369 0 84
#> Dmic 0 0 6 60 4 0 0 0 2758 319 25 0 329
#> Dmin 0 84 344 1045 90 0 0 0 8 0 0 0 0
fitofis <- c(rep(1, 4), rep(2, 4), rep(3, 4), rep(4, 4), rep(5, 4))
## Análise de espécies indicadoras
res_indval <- indval(t(sp_compos), fitofis)
# A função summary só exibe o resultado para as espécies indicadoras
summary(res_indval)
#> cluster indicator_value probability
#> Rict 1 0.8364 0.011
#> Sduar 1 0.7475 0.034
#> Bahe 2 0.6487 0.048
#>
#> Sum of probabilities = 7.984
#>
#> Sum of Indicator Values = 7.3
#>
#> Sum of Significant Indicator Values = 2.23
#>
#> Number of Significant Indicators = 3
#>
#> Significant Indicator Distribution
#>
#> 1 2
#> 2 1Para apresentar uma tabela dos resultados para todas as espécies temos de processar os dados.
## Resultados
tab_indval <- cbind.data.frame(maxcls = res_indval$maxcls,
ind.value = res_indval$indcls,
P = res_indval$pval)
tab_indval
#> maxcls ind.value P
#> Aper 3 0.2432796 1.000
#> Bahe 2 0.6487329 0.048
#> Rict 1 0.8363823 0.011
#> Cleuco 3 0.4128631 0.385
#> Dmic 3 0.6645244 0.195
#> Dmin 1 0.7032145 0.101
#> Hpoly 2 0.6208711 0.259
#> Lfur 3 0.2279412 1.000
#> Pbar 1 0.2813725 0.624
#> Polf 3 0.2437500 1.000
#> Pmelano 2 0.2500000 1.000
#> Sduar 1 0.7474527 0.034
#> Shay 3 0.4930269 0.416
#> Sobt 2 0.2222222 0.683
#> Ssqual 3 0.2500000 1.000
#> Bokerm 2 0.4583333 0.228
## Espécies
tab_indval[tab_indval$P < 0.05, ]
#> maxcls ind.value P
#> Bahe 2 0.6487329 0.048
#> Rict 1 0.8363823 0.011
#> Sduar 1 0.7474527 0.034Interpretação dos resultados
No resultado apresentado, podemos ver que temos duas espécies indicadoras da fitofisionimia 1: Rhinella icterica (Rict) e Scinax duartei (Sduar). Nenhuma espécie foi indicadora dos outros grupos neste exemplo.
9.3 Análises de Ordenação
As análises de ordenação representam um conjunto de métodos e técnicas multivariadas que organizam objetos (e.g., localidades, indivíduos) em alguma ordem considerando o conjunto de descritores que podem estar mais ou menos relacionados entre si. Se os descritores estiverem bem relacionados, eles são redundantes e organizam os objetos de forma similar. Esse fenômeno é observado, por exemplo, quando queremos organizar um conjunto de unidades amostrais baseado em variáveis que indicam um mesmo processo: ver o padrão de similaridade geral de lagos usando várias variáveis relacionadas com a produtividade do sistema: clorofila-a, concentração de fósforo, nitrogênio, entre outros. Por exemplo, tais métodos permitem identificar se existem grupo de espécies que ocorrem exclusivamente em um determinado hábitat. Ao buscar esta ordem, as técnicas de ordenação possuem três principais utilidades: i) reduzir a dimensionalidade e revelar padrões, ii) separar as variáveis mais e menos importantes em combinações complexas e iii) separar relações mais e menos fortes ao comparar variáveis preditoras e dependentes.
Em geral, os métodos são divididos em ordenações irrestritas (ou análise de gradiente indireto) e restritas (ou análise de gradiente direto). As ordenações irrestritas organizam os objetos (e.g., espécies) de acordo com sua estrutura de covariância (ou correlação), o que demonstra que a proximidade (ou distância) dentro do espaço multidimensional representa semelhança (ou diferença) dos objetos. Por outro lado, as ordenações restritras posicionam os objetos (e.g., espécies) de acordo com sua relação linear com outras variáveis coletadas nas mesmas unidades amostrais (e.g., temperatura e precipitação). Ao passo que as ordenações irrestritas dependem somente de uma matriz (e.g., espécies por localidades), as ordenações restritas utilizam no mínimo duas matrizes (e.g., espécies por localidades e variáveis climáticas por localidade). Desse modo, fica claro esta diferença entre os dados utilizados que as análises irrestritas são mais exploratórias, enquanto análises restritas são ideais para testar hipóteses com dados multidimensionais. A tabela a seguir apresenta as principais análises utilizadas em ecologia.
| Método | Tipo de variável | Função R |
|---|---|---|
| Ordenação irrestrita | ||
| PCA | Variáveis contínuas (distância euclidiana) |
PCA(), rda(), dudi.pca()
|
| PCoA | Aceita qualquer tipo de variável, mas depende da escolha apropriada de uma medida de distância |
pcoa(), dudi.pco()
|
| nMDS | Aceita qualquer tipo de variável, mas depende da escolha apropriada de uma medida de distância |
metaMDS(), nmds()
|
| CA | dudi.coa() |
|
| Hill-Smith | Aceita qualquer tipo de variável | dudi.hillsmith() |
| Ordenação restrita | ||
| RDA | Variáveis preditoras de qualquer tipo e variáveis dependentes contínuas (ou presença e ausência) | rda() |
| RDA parcial | Variáveis preditoras de qualquer tipo e variáveis dependentes contínuas (ou presença e ausência) | rda() |
| dbRDA | Variáveis preditoras de qualquer tipo e matriz de distância obtida a partir das variáveis dependentes |
capscale(), dbrda()
|
| CCA | Variáveis preditoras de qualquer tipo e variáveis dependentes contínuas (ou presença e ausência) | rda() |
| PERMANOVA | Variáveis preditoras de qualquer tipo e matriz de distância obtida a partir das variáveis dependentes |
adonis(), adonis2()
|
| PCR | Variável dependente necessariamente representada por escores da PCA ou PCoA e variáveis preditoras de qualquer tipo |
pca(), pcoa(), lm(), glm()
|
9.4 Ordenação irrestrita
Ordenações irrestritas, ou análise de gradiente indireto ou ainda análises de fator, são um conjunto de métodos multivariados que lidam com uma única matriz quadrada. Esta matriz pode ou não ter pesos nas linhas ou colunas. Geralmente, o objetivo deste tipo de análise é resumir a informação contida na matriz de maneira gráfica, por meio de um diagrama de ordenação. Quanto maior e mais complexa for a matriz, mais eficiente é este tipo de análise. Os tipos de análise irão diferir de acordo com o tipo de dado contido nesta matriz, se contínuo ou contagem, etc. De maneira geral, essas ordenações irrestritas calculam combinações lineares, cuja formulação irá diferir ligeiramente entre os métodos. Da mesma forma, essas combinações lineares irão preservar um tipo de distância. Por exemplo, a Análise de Componentes Principais preserva a distância Euclidiana, enquanto a Análise de Correspondência preserva a distância de chi-quadrado.
9.4.1 Análise de Componentes Principais (PCA)
A Análise de Componentes Principais (Principal Component Analysis - PCA) é uma das ordenações mais utilizadas em diversas áreas do conhecimento. Em Ecologia, ela se popularizou por facilitar a visualização de dados complexos como de distribuição de espécies em diferentes localidades e de potenciais variáveis explicativas. Ao mesmo tempo que ganhou tamanha popularidade, a PCA tem sido empregada de maneira incorreta, uma vez que muitos estudos utilizam a visualização gráfica da ordenação (o biplot) para interpretar “relações” entre variáveis preditoras (ambientais) e dependentes (espécies). Porém, como informado anteriormente, as ordenações irrestritas utilizam a estrutura de covariância dos objetos para organizar suas relações de similaridade.
Antes de explicar a análise, imagine que vamos usar uma matriz com cinco espécies de aranhas que foram encontradas em oito cidades diferentes. A quantidade de indivíduos de cada espécie coletada em cada cidade será o valor de preenchimento desta matriz. Sendo assim, a matriz possui oito objetos (cidades, representando unidades amostrais) e cinco descritores (espécies).
| Cidade | Espécie.1 | Espécie.2 | Espécie.3 | Espécie.4 | Espécie.5 |
|---|---|---|---|---|---|
| Cidade 1 | 5 | 0 | 0 | 0 | 0 |
| Cidade 2 | 7 | 6 | 0 | 0 | 0 |
| Cidade 3 | 2 | 3 | 0 | 0 | 0 |
| Cidade 4 | 0 | 4 | 9 | 0 | 0 |
| Cidade 5 | 0 | 0 | 12 | 4 | 0 |
| Cidade 6 | 0 | 0 | 3 | 10 | 6 |
| Cidade 7 | 0 | 0 | 0 | 8 | 9 |
| Cidade 8 | 0 | 0 | 0 | 0 | 12 |
O primeiro passo da PCA é obter uma matriz centralizada, onde cada valor é subtraído da média da coluna que aquele valor pertence. Esta centralização pode ser calculada com a função scale().
## Dados
aranhas <- data.frame(
sp1 = c(5, 7, 2, 0, 0, 0, 0, 0),
sp2 = c(0, 6, 3, 4, 0, 0, 0, 0),
sp3 = c(0, 0, 0, 9, 12, 3, 0, 0),
sp4 = c(0, 0, 0, 0, 4, 10, 8, 0),
sp5 = c(0, 0, 0, 0, 0, 6, 9, 12),
row.names = paste0("cidade", 1:8))
## Centralização
aranha.cent <- as.data.frame(base::scale(aranhas, center = TRUE, scale=FALSE))O segundo passo é calcular uma matriz de covariância (ou matriz de dispersão) e, a partir desta matriz, obter os autovalores e autovetores. Os autovalores representam a porcentagem de explicação de cada eixo e podem ser calculados dividindo a soma do autovalor de cada eixo pela soma de todos os autovalores. No exemplo que apresentamos, os dois primeiros eixos representam 47,20% e 35,01% de toda variação, respectivamente. Os autovetores, por sua vez, representam os valores que multiplicam as variáveis originais e, desse modo, indicam a direção desses valores. Por fim, os componentes principais (Matriz F) são obtidos multiplicando os autovetores com os valores da matriz centralizada.
## Matriz de covaiância
matriz_cov <- cov(aranha.cent)
## Autovalores e autovetores
eigen_aranhas <- eigen(matriz_cov)
autovalores <- eigen_aranhas$values
autovetores <- as.data.frame(eigen_aranhas$vectors)
autovalores # eigenvalue
#> [1] 36.733031 27.243824 9.443805 2.962749 1.438020
colnames(autovetores) <- paste("PC", 1:5, sep="")
rownames(autovetores) <- colnames(aranhas)
autovetores
#> PC1 PC2 PC3 PC4 PC5
#> sp1 -0.2144766 -0.38855265 -0.29239380 -0.02330706 0.8467522
#> sp2 -0.2442026 -0.17463316 -0.01756743 0.94587037 -0.1220204
#> sp3 -0.3558368 0.80222917 0.27591770 0.10991178 0.3762942
#> sp4 0.4159852 0.41786654 -0.78820962 0.17374202 0.0297183
#> sp5 0.7711688 -0.01860152 0.46560957 0.25003826 0.3544591
## Componentes principais
matriz_F <- as.data.frame(as.matrix(aranha.cent) %*% as.matrix(autovetores))
matriz_F
#> PC1 PC2 PC3 PC4 PC5
#> cidade1 -2.979363 -4.4720575 -1.1533417 -3.2641923 0.5433206
#> cidade2 -4.873532 -6.2969618 -1.8435339 2.3644158 1.5047024
#> cidade3 -3.068541 -3.8302991 -0.3288626 -0.3566600 -2.3629973
#> cidade4 -6.086322 3.9922356 2.7216169 1.6250305 -0.7918743
#> cidade5 -4.513082 8.7689219 0.4668012 -1.1337476 0.9439633
#> cidade6 5.812374 3.9444494 -3.9520584 0.4197281 -0.1376205
#> cidade7 8.361421 0.6462243 -1.8065636 0.4926235 -0.2625625
#> cidade8 7.347046 -2.7525126 5.8959421 -0.1471979 0.5630683
## Porcentagem de explicação de cada eixo
100 * (autovalores/sum(autovalores))
#> [1] 47.201691 35.008126 12.135225 3.807112 1.847846Agora, é possível visualizar a relação entre as cidades e similaridade nas espécies de aranhas que vivem em cada uma delas (Figura 9.6).
## Gráfico
ggplot(matriz_F, aes(x = PC1, y = PC2, label = rownames(matriz_F))) +
geom_label() +
geom_hline(yintercept = 0, linetype=2) +
geom_vline(xintercept = 0, linetype=2) +
xlim(-10, 10) +
tema_livro()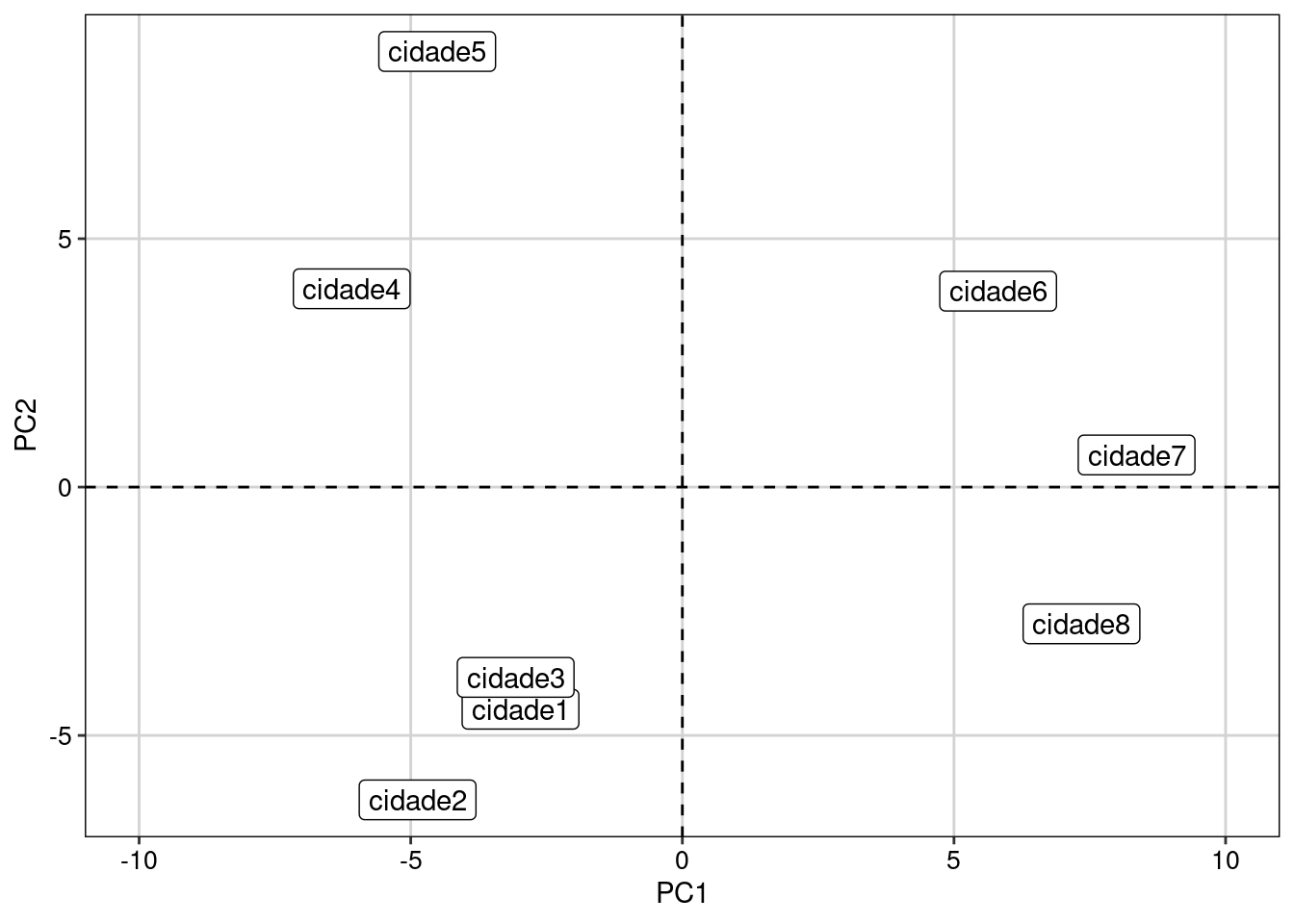
Figura 9.6: Biplot da PCA ordenando as cidades pela composição das espécies de aranhas.
Checklist
Verifique se todas as variáveis utilizadas são contínuas. Caso contrário, considere utilizar PCoA (veja mais no próximo tópico)
Apesar do exemplo acima ter apresentado a ocorrência de espécies de aranhas em diferentes cidades, é fundamental saber que utilizar a PCA com esses dados pode ser problemático. Assim, tenha cuidado em usar dados de composição de espécies, especialmente abundância, com PCA, uma vez que ‘duplos zeros’ podem gerar distorções na ordenação (Legendre and Legendre 2012). Como alternativa, é possível utilizar PCA com dados padronizados com o método de Hellinger (Legendre and Gallagher 2001).
Exemplo 1
Neste exemplo vamos utilizar um conjunto de dados morfológicos de pinguins do arquipélago Palmer (Península Antártica) disponíveis no pacote palmerpenguins. Os dados representam medidas do comprimento e largura do bico (mm), comprimento da nadadeira (mm) e massa corporal (gramas) de três espécies: Adélie, Chinstrap e Gentoo. Como descrito acima, a PCA deve ser utilizada para exploração de dados ou para testes a posteriori (e.g., Regressão de Componentes Principais - PCR, tópico explorado mais a frente nesse capítulo). Neste exemplo, iremos usar a estrutura de perguntas e predições para manter a proposta do livro.
Pergunta
- Existe diferenças nas características morfológicas das espécies de pinguins do arquipélago Palmer?
Predições
- Pinguins com dieta diferente possuem diferentes características morfológicas
Variáveis
- Preditora: espécie (categórica com três níveis)
- Dependentes: variáveis morfológicas (contínua)
Análises
Antes de começar, é necessário remover dados ausentes (se houver) e editar nomes das variáveis (ponto importante para determinar como devem aparecer no gráfico).
## Verificar se existem NAs nos dados
sum(is.na(penguins))
#> [1] 19
## Remover dados ausentes (NA), quando houver
penguins <- na.omit(penguins)
## Manter somentes dados contínuos que pretende aplicar a PCA
penguins_trait <- penguins[, 3:6]Agora sim, os dados estão prontos para fazer a PCA. Um argumento é essencial na análise, o scale.unit. Se você utilizar dentro deste argumento a seleção TRUE, a função padroniza automaticamente as variáveis para terem a média 0 e variância 1. Esta padronização é essencial quando as variáveis estão em escalas muito diferentes. No exemplo selecionado, temos variáveis como comprimento do bico (em milímetros) e massa corporal (em gramas).
## Compare com este código a variância das variáveis
penguins_trait %>%
dplyr::summarise(across(where(is.numeric),
~var(.x, na.rm = TRUE)))
#> # A tibble: 1 × 4
#> comprimento_bico profundidade_bico comprimento_nadadeira massa_corporal
#> <dbl> <dbl> <dbl> <dbl>
#> 1 29.9 3.88 196. 648372.
## Agora, veja o mesmo cálculo se fizer a padronização (scale.unit da função PCA)
penguins_pad <- decostand(x = penguins_trait, method = "standardize")
penguins_pad %>%
dplyr::summarise(across(where(is.numeric),
~var(.x, na.rm = TRUE)))
#> comprimento_bico profundidade_bico comprimento_nadadeira massa_corporal
#> 1 1 1 1 1
## PCA
pca.p <- PCA(X = penguins_trait, scale.unit = TRUE, graph = FALSE)Apesar da simplicidade do código para executar a PCA, o objeto resultante da análise possui diversas informações que são essenciais para sua plena interpretação. Dentre elas, se destacam os autovalores, escores e cargas (loadings). Os autovalores representam a porcentagem de explicação de cada eixo. Os escores representam as coordenadas (posições no espaço multidimensional) representando os objetos (geralmente localidades ou indivíduos) e descritores (geralmente espécies ou variáveis ambientais e espaciais). Os loadings, por sua vez, representam a combinação linear entre os escores (nova posição do valor do descritor no espaço ordenado) e os valores originais dos descritores (Figura 9.7).
## Autovalores: porcentagem de explicação para usar no gráfico
pca.p$eig
#> eigenvalue percentage of variance cumulative percentage of variance
#> comp 1 2.7453557 68.633893 68.63389
#> comp 2 0.7781172 19.452929 88.08682
#> comp 3 0.3686425 9.216063 97.30289
#> comp 4 0.1078846 2.697115 100.00000
## Visualização da porcentagem de explicação de cada eixo
# nota: é necessário ficar atento ao valor máximo do eixo 1 da análise para determinar o valor do ylim (neste caso, colocamos que o eixo varia de 0 a 70).
fviz_screeplot(pca.p, addlabels = TRUE, ylim = c(0, 70), main = "",
xlab = "Dimensões",
ylab = "Porcentagem de variância explicada")
## Outros valores importantes
var_env <- get_pca_var(pca.p)
## Escores (posição) das variáveis em cada eixo
var_env$coord
#> Dim.1 Dim.2 Dim.3 Dim.4
#> comprimento_bico 0.7518288 0.52943763 -0.3900969 -0.04768208
#> profundidade_bico -0.6611860 0.70230869 0.2585287 0.05252186
#> comprimento_nadadeira 0.9557480 0.00510580 0.1433474 0.25684871
#> massa_corporal 0.9107624 0.06744932 0.3592789 -0.19204478
## Contribuição (%) das variáveis para cada eixo
var_env$contrib
#> Dim.1 Dim.2 Dim.3 Dim.4
#> comprimento_bico 20.58919 36.023392267 41.279994 2.107420
#> profundidade_bico 15.92387 63.388588337 18.130600 2.556942
#> comprimento_nadadeira 33.27271 0.003350291 5.574092 61.149849
#> massa_corporal 30.21423 0.584669105 35.015313 34.185789
## Loadings - correlação das variáveis com os eixos
var_env$cor
#> Dim.1 Dim.2 Dim.3 Dim.4
#> comprimento_bico 0.7518288 0.52943763 -0.3900969 -0.04768208
#> profundidade_bico -0.6611860 0.70230869 0.2585287 0.05252186
#> comprimento_nadadeira 0.9557480 0.00510580 0.1433474 0.25684871
#> massa_corporal 0.9107624 0.06744932 0.3592789 -0.19204478
## Qualidade da representação da variável. Esse valor é obtido multiplicado var_env$coord por var_env$coord
var_env$cos2
#> Dim.1 Dim.2 Dim.3 Dim.4
#> comprimento_bico 0.5652466 2.803042e-01 0.15217561 0.002273581
#> profundidade_bico 0.4371669 4.932375e-01 0.06683710 0.002758546
#> comprimento_nadadeira 0.9134542 2.606919e-05 0.02054847 0.065971260
#> massa_corporal 0.8294881 4.549411e-03 0.12908133 0.036881196
## Escores (posição) das localidades ("site scores") em cada eixo
ind_env <- get_pca_ind(pca.p)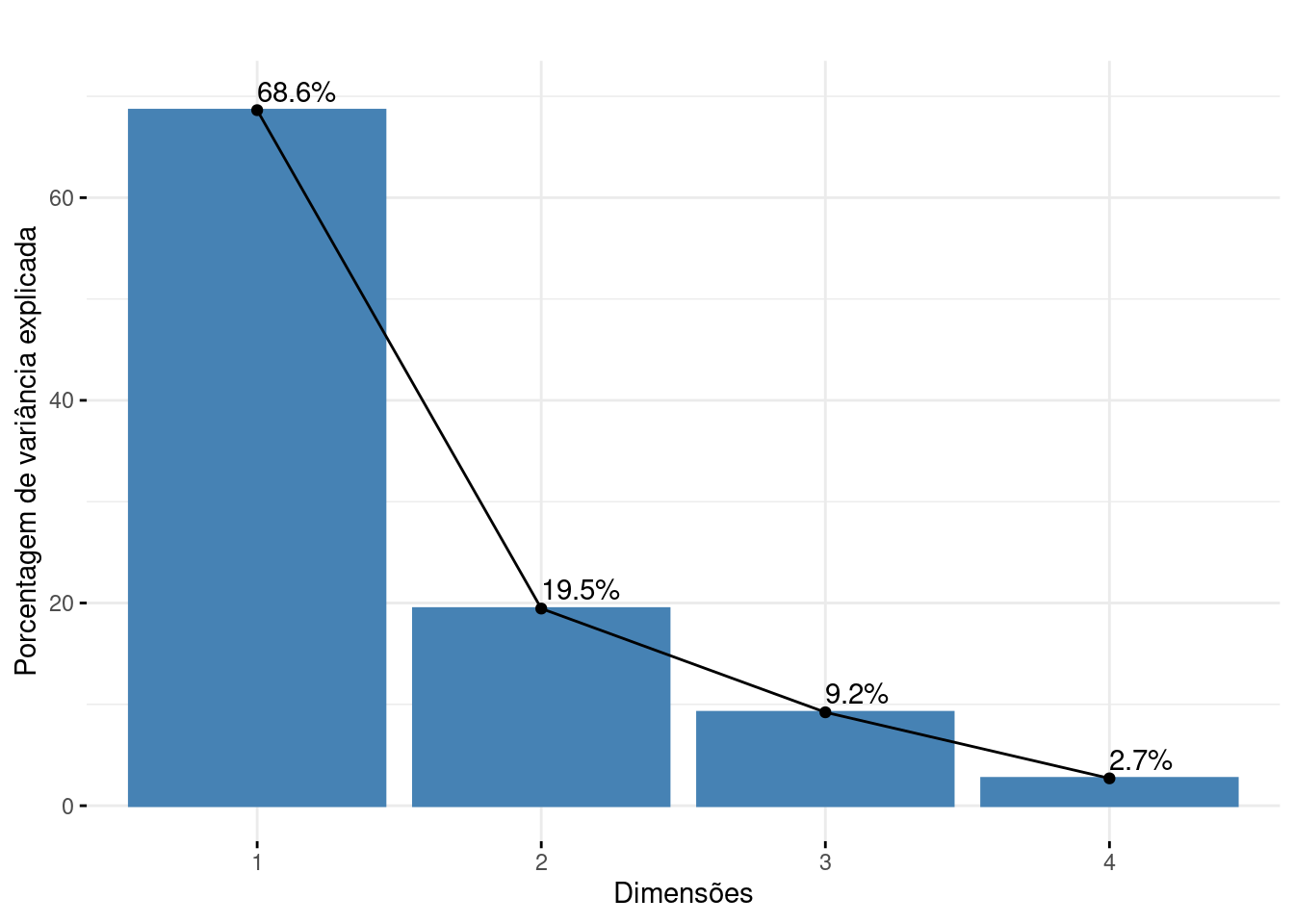
Figura 9.7: Scree plot mostrando a porcentagem de contribuição de cada eixo para a ordenação dos dados de penguins.
O pacote FactoMineR criou uma função (dimdesc()) que seleciona as melhores variáveis (aquelas mais explicativas) para cada eixo através de uma análise fatorial. No exemplo com pinguins, o primeiro eixo (objeto pca.p$eig) explica ~69% da variação morfológica. A função dimdesc() mostra que as quatro variáveis morfológicas estão fortemente associadas com o eixo 1. Porém, enquanto comprimento da nadadeira, massa corporal e comprimento do bico estão positivamente associados com o eixo 1 (correlação positiva), a largura do bico tem relação negativa. O eixo 2, por sua vez, explica ~20% da variação, sendo relacionado somente com largura e comprimento do bico.
## Variáveis mais importantes para o Eixo 1
dimdesc(pca.p)$Dim.1
#> $quanti
#> correlation p.value
#> comprimento_nadadeira 0.9557480 5.962756e-178
#> massa_corporal 0.9107624 3.447018e-129
#> comprimento_bico 0.7518288 7.830597e-62
#> profundidade_bico -0.6611860 3.217695e-43
#>
#> attr(,"class")
#> [1] "condes" "list"
## Variáveis mais importantes para o Eixo 2
dimdesc(pca.p)$Dim.2
#> $quanti
#> correlation p.value
#> profundidade_bico 0.7023087 8.689230e-51
#> comprimento_bico 0.5294376 1.873918e-25
#>
#> attr(,"class")
#> [1] "condes" "list"Agora podemos utilizar o famoso biplot para representar a comparação morfológica dos pinguins dentro e entre espécies (Figura 9.8).
fviz_pca_biplot(X = pca.p,
geom.ind = "point",
fill.ind = penguins$especies,
col.ind = "black",
alpha.ind = 0.7,
pointshape = 21,
pointsize = 4,
palette = c("darkorange", "darkorchid", "cyan4"),
col.var = "black",
invisible = "quali",
title = NULL) +
labs(x = "PC1 (68.63%)", y = "PC2 (19.45%)") +
xlim(c(-4, 5)) +
ylim(c(-3, 3)) +
tema_livro()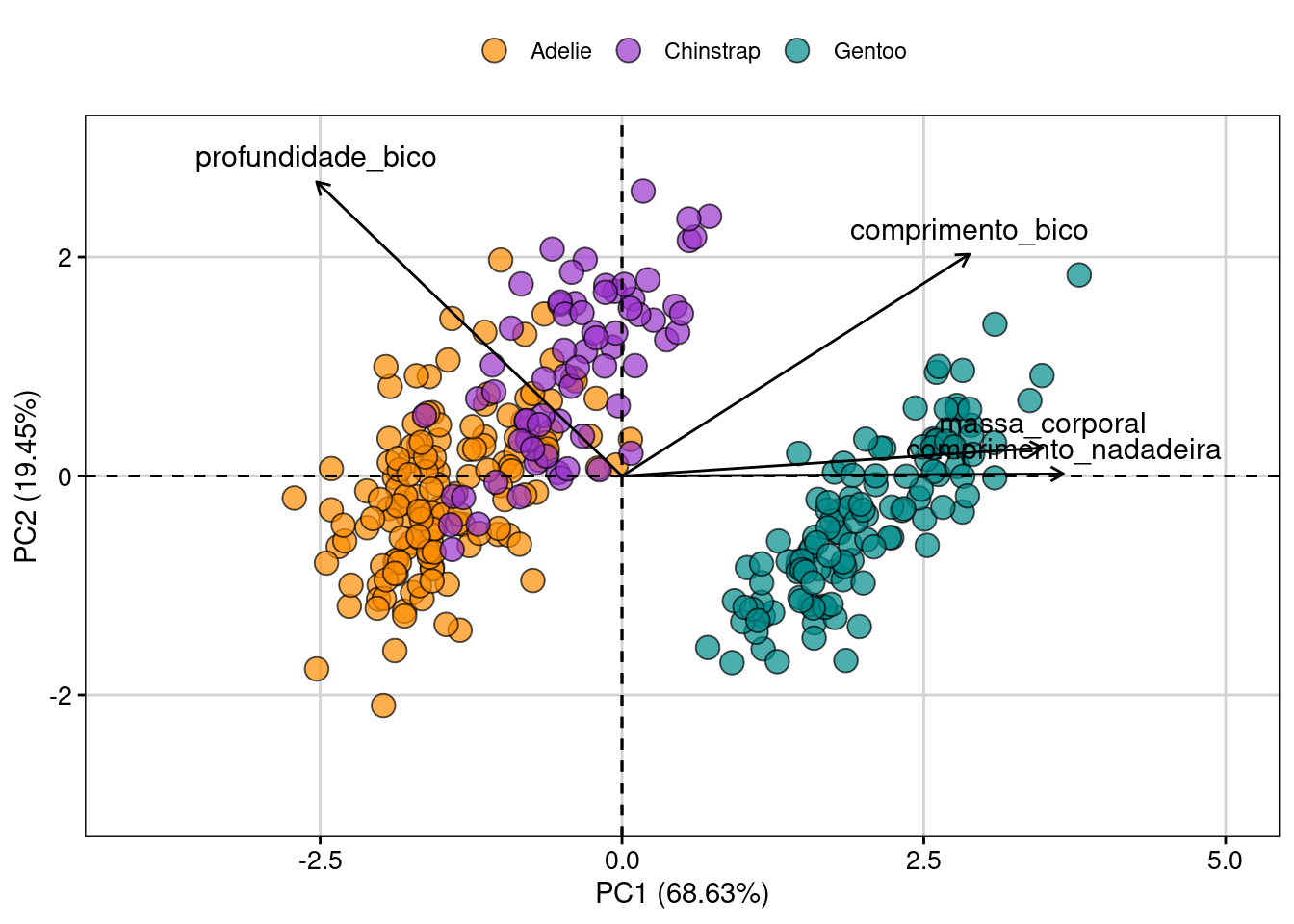
Figura 9.8: Biplot da PCA ordenando os dados morfológicos de penguins.
9.4.2 Análises de Coordenadas Principais (PCoA)
Diferentemente da PCA, a Análises de Coordenadas Principais (Principal Coordinate Analysis - PCoA) é uma análise de ordenação irrestrita que aceita dados de diferentes tipos, como contínuos, categóricos, ordinais, binários, entre outros. Assim, a PCoA é aplicada para casos em que a distância euclidiana não é aplicada (como na PCA). Desse modo, o primeiro passo da análise é calcular uma matriz de similaridade ou de distância (discutido acima). Depois, os passos para obter autovalores e autovetores são bastante parecidos com a PCA. Da mesma forma, os eixos da PCoA e os valores ou posições dos objetos nesses eixos representam a relação de semelhança (ou diferença) baseada nos descritores desses objetos. A diferença, neste caso, é que a PCoA representa um espaço não-euclidiano, que irá ser afetado pela escolha do método de similaridade.
As utilizações mais comuns da PCoA são a ordenação: i) da matriz de composição de espécies usando a distância apropriada (Jaccard, Sorensen, Bray-Curtis), ii) da matriz de variáveis ambientais com mistos (contínuos, categóricos, circulares, etc.), e iii) da matriz filogenética, método PVR (Diniz-Filho, de Sant’Ana, and Bini 1998). Abaixo, exemplificamos a ordenação da matriz de composição de espécies.
Checklist
Compare as dimensões das matrizes utilizadas para a PCoA. Com bastante frequência, a tentativa de combinar dados categóricos (algum descritor dos objetos) com os valores obtidos com a PCoA gera erros para plotar a figura ou para executar a análise. Verifique, então, se as linhas são as mesmas (nome das localidades ou indivíduos e quantidade)
É fundamental conhecer o tipo de dados que está usando para selecionar a medida de distância apropriada. Essa escolha vai afetar a qualidade da ordenação e sua habilidade para interpretar a relação de semelhança entre os objetos comparados
Diferente da PCA, a PCoA aceita dados ausentes se a medida de distância escolhida também não tiver esta limitação. Por exemplo, a distância de Gower produz matrizes de similaridade mesmo com dados ausentes em determinados objetos
Em alguns casos, autovalores negativos são produzidos na ordenação com PCoA. Veja as principais causas desses valores em Legendre & Legendre (2012). Apesar deste problema, os autovalores mais importantes (eixos iniciais) não são afetados e, deste modo, a qualidade da representação dos objetos no espaço multidimensional não é afetada. Alguns autores sugerem utilizar correções métodos de correção, como Lingoes ou Cailliez (Legendre and Legendre 2012).
Exemplo 1
Neste exemplo, vamos utilizar a composição de ácaros Oribatidae em 70 manchas de musgo coletados por Borcard et al. (1992).
Pergunta
- A composição de espécies de ácaros muda entre diferentes topografias?
Predições
- Iremos encontrar ao menos dois grupos de espécies: aquelas que ocorrem em poças dentro de floresta versus aquelas que ocorrem em poças de áreas abertas
Variáveis
- Preditora: topografia (categórica com dois níveis)
- Dependentes: composição de espécies de ácaro
Análises
Vamos primeiramente padronizar dos dados, calcular uma matriz de distância com método Bray-Curtis e depois calcular a PCoA.
## Padronização dos dados com Hellinger
mite.hel <- decostand(x = mite, method = "hellinger")
## Cálculo da matriz de distância com método Bray-Curtis
sps.dis <- vegdist(x = mite.hel, method = "bray")
## PCoA
pcoa.sps <- pcoa(D = sps.dis, correction = "cailliez")Assim como na PCA, a porcentagem de explicação dos eixos é uma das informações mais importantes pois descrevem a efetividade da redução da dimensionalidade dos dados.
## Porcentagem de explicação do Eixo 1
100 * (pcoa.sps$values[, 1]/pcoa.sps$trace)[1]
#> [1] 49.10564
## Porcentagem de explicação dos Eixo 2
100 * (pcoa.sps$values[, 1]/pcoa.sps$trace)[2]
#> [1] 14.30308
## Porcentagem de explicação acumulada dos dois primeiros eixos
sum(100 * (pcoa.sps$values[, 1]/pcoa.sps$trace)[1:2])
#> [1] 63.40872
## Selecionar os dois primeiros eixos
eixos <- pcoa.sps$vectors[, 1:2]
## Juntar com algum dado categórico de interesse para fazer a figura
pcoa.dat <- data.frame(topografia = mite.env$Topo, eixos)Para visualizar os resultados da PCoA, vamos exportar os escores dos eixos para usar no pacote ggplot2 (Figura 9.9).
## Escores dos dois primeiros eixos
eixos <- pcoa.sps$vectors[, 1:2]
## Combinar dados dos escores com um dado categórico de interesse para nossa pergunta
pcoa.dat <- data.frame(topografia = mite.env$Topo, eixos)
### Gráfico biplot da PCoA
ggplot(pcoa.dat, aes(x = Axis.1, y = Axis.2, fill = topografia,
color = topografia, shape = topografia)) +
geom_point(size = 4, alpha = 0.7) +
scale_shape_manual(values = c(21, 22)) +
scale_color_manual(values = c("black", "black")) +
scale_fill_manual(values = c("darkorange", "cyan4")) +
labs(x = "PCO 1 (49.11%)", y = "PCO 2 (14.30%)") +
geom_hline(yintercept = 0, linetype = 2) +
geom_vline(xintercept = 0, linetype = 2) +
tema_livro()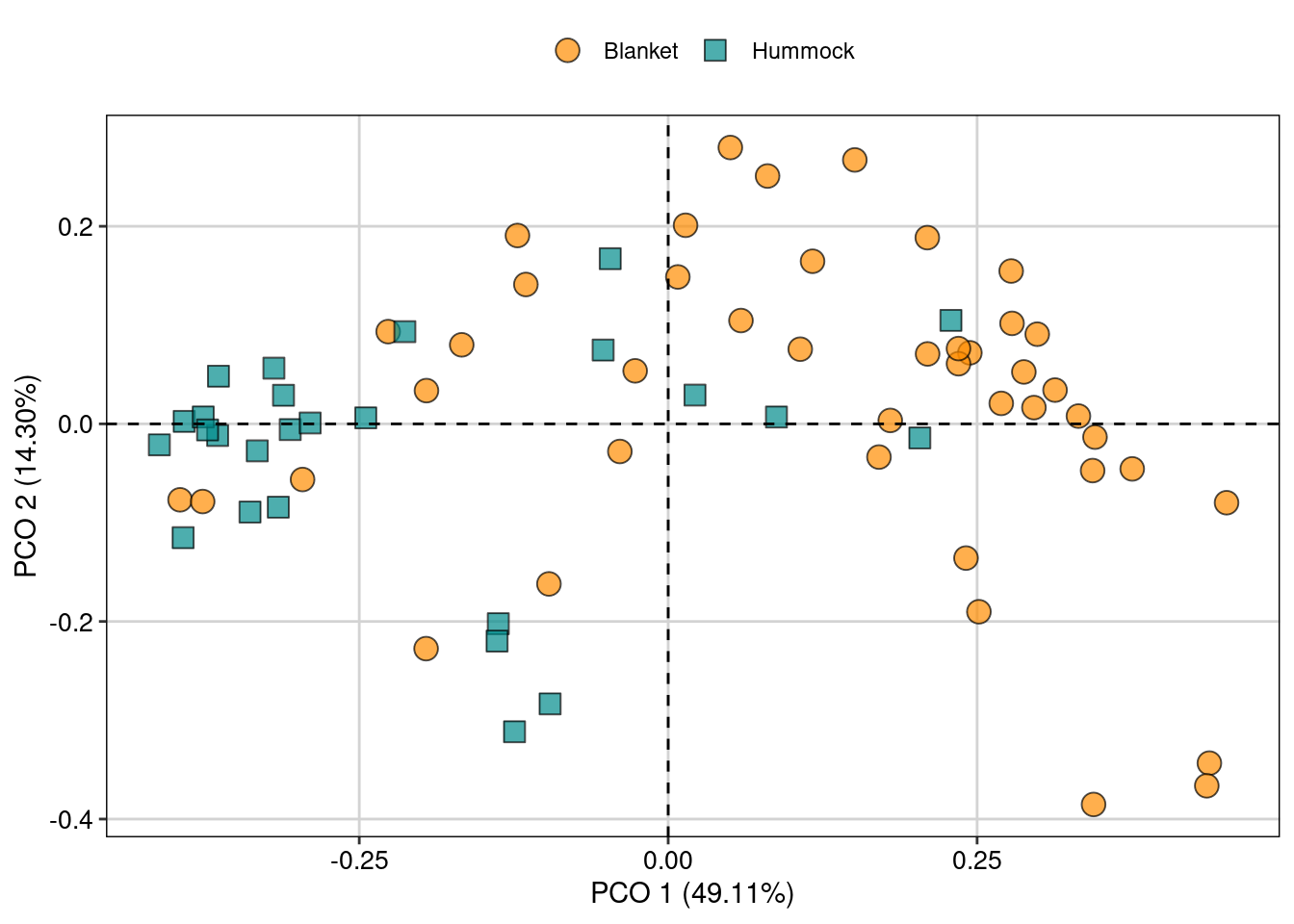
Figura 9.9: Biplot da PCoA ordenando as espécies de ácaros entre diferentes topografias.
Limitações importantes das ordenações irrestritas
Com frequência, pesquisadores utilizam análises como PCA e PCoA para “testar” diferenças na composição de espécies entre determinados fatores relevantes (altitude, clima, etc.). Porém, como falado acima, as análises de ordenação irrestritas não são utilizadas para testar qualquer hipótese. Ao invés disso, essas análises representam uma poderosa ferramente para explorar padrões em variáveis dependentes ou independentes para ajudar na interpretação ou mesmo para testar hipóteses em análises combinadas com as ordenações restritas.
9.4.3 Regressão de Componentes Principais (PCR)
Uma maneira de testar hipóteses utilizando ordenações irrestritas é utilizando os resultados da ordenação (escores) como variáveis preditoras ou dependentes como, por exemplo, em modelos lineares (e.g., regressão múltipla Capítulo 7). O primeiro passo é utilizar uma ordenação, como a PCA, para gerar os “novos” dados que serão usados na análise. A utilização desses novos dados (que representam as coordenadas principais ou escores da PCA) vai depender da pergunta em questão. Por exemplo, pode ser que esses valores representem gradientes climáticos e, por este motivo, serão utilizados como variáveis preditoras em um modelo linear (e.g., regressão múltipla). Por outro lado, esses valores podem representar o espaço morfológicos de espécies de peixes e, como consequência, serão utilizados como variáveis dependentes para entender o efeito da presença de predador sobre a morfologia. É importante ressaltar que existem algumas limitações importantes na PCR como, por exemplo, as coordenadas principais (escores da PCA) utilizadas como variáveis preditoras podem não representar, biologicamente, as mais importantes para explicar a variação na variável resposta (Hadi and Ling 1998).
Checklist
Compare as dimensões das matrizes utilizadas para a PCR. Com bastante frequência, a tentativa de combinar dados categóricos (algum descritor dos objetos) com os valores obtidos com a PCoA gera erros para plotar a figura ou para executar a análise. Verifique, então, se as linhas são as mesmas (nome das localidades ou indivíduos e quantidade)
Estudos recentes têm criticado a utilização de PCR para testar hipóteses ecológicas pelo fato dos escores não representarem, necessariamente, a variação total das variáveis originais, bem como a relação entre a variável preditora e a dependente
Exemplo 1
Neste exemplo, vamos utilizar a composição de espécies de aves em 23 regiões dos alpes franceses. Os dados ambientais (env) representam variáveis climáticas (temperatura e chuva) e altitude.
Pergunta
- Gradientes climáticos afetam a riqueza de aves?
Predições
- O aumento da umidade e redução da temperatura aumentam o número de espécies de aves
Variáveis
- Preditora: temperatura e chuva (contínuas) e altitude (categórica com três níveis)
- Dependentes: riqueza de espécies de aves
## Dados
env_cont <- env[,-8]
env.pca <- PCA(env_cont, scale.unit = TRUE, graph = FALSE)
var_env <- get_pca_var(env.pca)
## Contribuição (%) das variáveis para cada eixo
var_env$contrib
#> Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
#> mini.jan 10.93489 22.2975487 16.1607726 7.6025527 0.01782438
#> maxi.jan 20.18065 3.2890767 2.1814486 4.2756350 41.05646526
#> mini.jul 11.87396 21.1379132 0.3428843 0.7750666 44.70209396
#> maxi.jul 18.47244 0.9159957 56.5369988 9.4368661 2.59283074
#> rain.jan 9.95206 21.5387403 6.5737927 53.7375738 4.44283706
#> rain.jul 16.14997 11.2368132 7.2608047 19.6972097 0.71454880
#> rain.tot 12.43603 19.5839121 10.9432983 4.4750959 6.47339980
## Loadings - correlação das variáveis com os eixos
var_env$cor
#> Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
#> mini.jan 0.6830371 0.6766524 -0.21924927 0.12298817 -0.004517369
#> maxi.jan 0.9279073 0.2598807 -0.08055260 0.09223249 0.216804944
#> mini.jul 0.7117620 0.6588220 0.03193603 -0.03926930 -0.226225907
#> maxi.jul 0.8877675 0.1371462 0.41008461 -0.13702428 0.054483561
#> rain.jan -0.6516187 0.6650391 -0.13983474 -0.32698110 0.071319550
#> rain.jul -0.8300858 0.4803509 0.14696011 0.19796389 -0.028601865
#> rain.tot -0.7284135 0.6341424 0.18041856 0.09435932 0.086088397
ind_env <- get_pca_ind(env.pca)
env.pca$eig
#> eigenvalue percentage of variance cumulative percentage of variance
#> comp 1 4.26652359 60.9503370 60.95034
#> comp 2 2.05340251 29.3343216 90.28466
#> comp 3 0.29745014 4.2492878 94.53395
#> comp 4 0.19896067 2.8422953 97.37624
#> comp 5 0.11448717 1.6355310 99.01177
#> comp 6 0.04312874 0.6161248 99.62790
#> comp 7 0.02604718 0.3721025 100.00000O objeto env.pca$eig demonstra que os três primeiros eixos explicam 94.54% da variação total dos dados climáticos. O intuito da PCR é reduzir a dimensionalidade, ou seja, o número de variáveis preditoras ou dependentes para facilitar a interpretação e garantir que as variáveis não sejam correlacionadas. O próximo passo então é obter os valores dos escores que representam os valores convertidos para serem usados em uma determinada análise, como a regressão múltipla.
## Passo 1: obter os primeiros eixos
pred.env <- ind_env$coord[, 1:3]
## Passo 2: calcular a riqueza de espécies
riqueza <- specnumber(species)
## Passo 3: combinar os dois valores em um único data.frame
dat <- data.frame(pred.env, riqueza) Agora que os dados foram combinados em uma única data frame, podemos utilizar os códigos apresentados no Capítulo 7 para testar nossa hipótese (Figura 9.10).
## Regressão múltipla
mod1 <- lm(riqueza ~ Dim.1 + Dim.2 + Dim.3, data = dat)
par(mfrow = c(2, 2))
plot(mod1) # verificar pressupostos dos modelos lineares
summary(mod1) # resultados do teste
#>
#> Call:
#> lm(formula = riqueza ~ Dim.1 + Dim.2 + Dim.3, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -3.4008 -1.1729 0.4356 1.2072 2.4571
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 13.30435 0.37639 35.347 < 2e-16 ***
#> Dim.1 0.68591 0.18222 3.764 0.00131 **
#> Dim.2 -0.09961 0.26267 -0.379 0.70874
#> Dim.3 -0.21708 0.69014 -0.315 0.75654
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.805 on 19 degrees of freedom
#> Multiple R-squared: 0.4313, Adjusted R-squared: 0.3415
#> F-statistic: 4.804 on 3 and 19 DF, p-value: 0.01179
dimdesc(env.pca)$Dim.1
#> $quanti
#> correlation p.value
#> maxi.jan 0.9279073 1.846790e-10
#> maxi.jul 0.8877675 1.607390e-08
#> mini.jul 0.7117620 1.396338e-04
#> mini.jan 0.6830371 3.282701e-04
#> rain.jan -0.6516187 7.559358e-04
#> rain.tot -0.7284135 8.112903e-05
#> rain.jul -0.8300858 9.588034e-07
#>
#> attr(,"class")
#> [1] "condes" "list"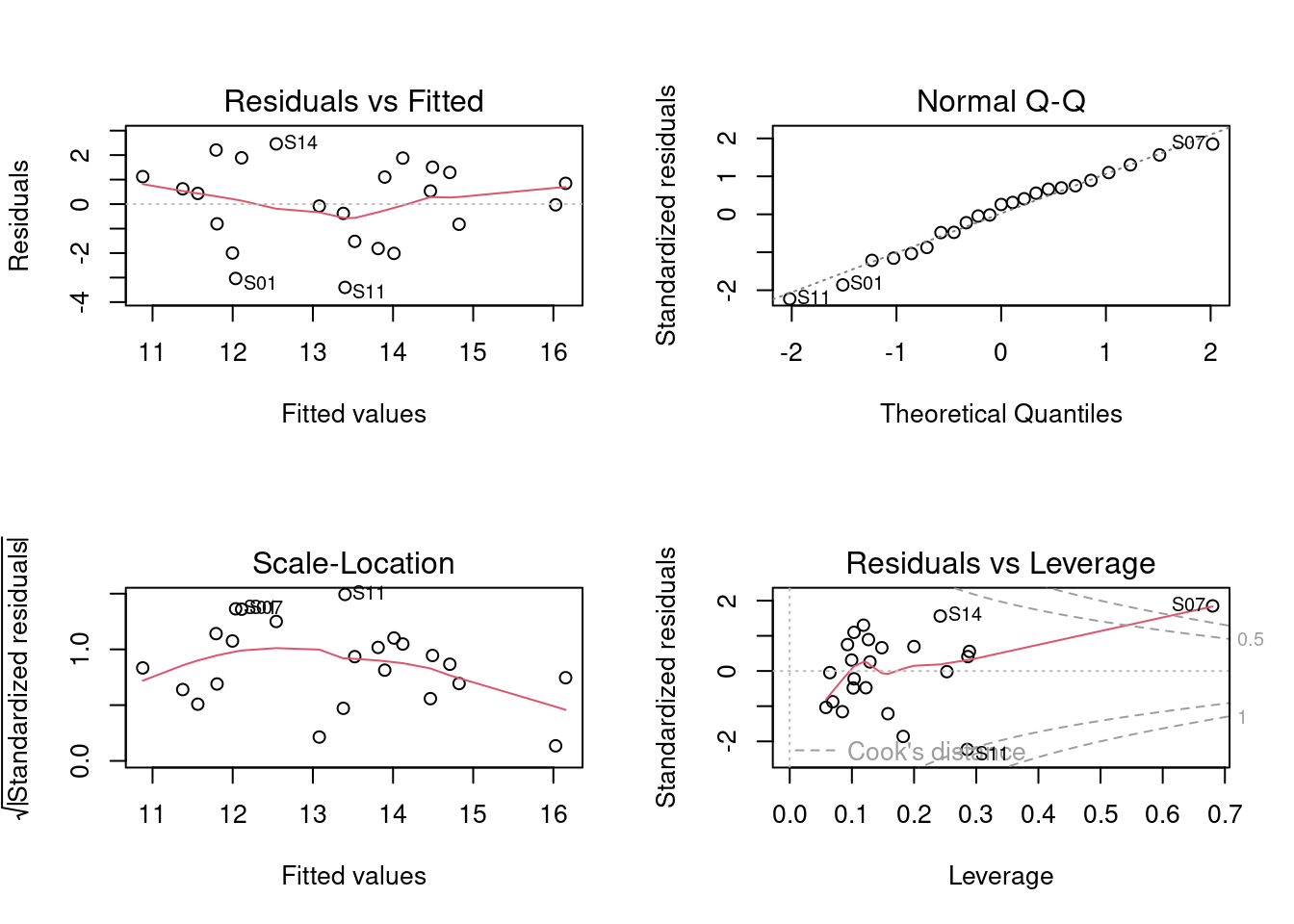
Figura 9.10: Diagnósticos dos modelo PCR para aves.
Como percebemos, a Dim.1 foi o único gradiente ambiental que afetou a riqueza de espécies. Para interpretar esta dimensão (e outras importantes), podemos usar a função dimdesc() para verificar as variáveis mais importantes. Neste caso, os valores mais extremos de correlação (maior que 0.8) indicam que a temperatura do mês de janeiro e julho bem como a chuva do mês de julho foram as variáveis mais importantes para determinar o gradiente ambiental expresso na dimensão 1. Assim, podemos fazer um gráfico para representar a relação entre Eixo 1 (gradiente chuva-temperatura) e a riqueza de espécies de aves. Valores negativos do eixo 1 (Gradiente ambiental - PC1) representam localidades com mais chuva, ao passo que valores positivos indicam localidades com temperaturas maiores (Figura 9.11).
ggplot(dat, aes(x = Dim.1, y = riqueza)) +
geom_smooth(method = lm, fill = "#525252", color = "black") +
geom_point(size = 4, shape = 21, alpha = 0.7, color = "#1a1a1a", fill = "cyan4") +
labs(x = "Gradiente ambiental (PC1)", y = "Riqueza de aves") +
tema_livro()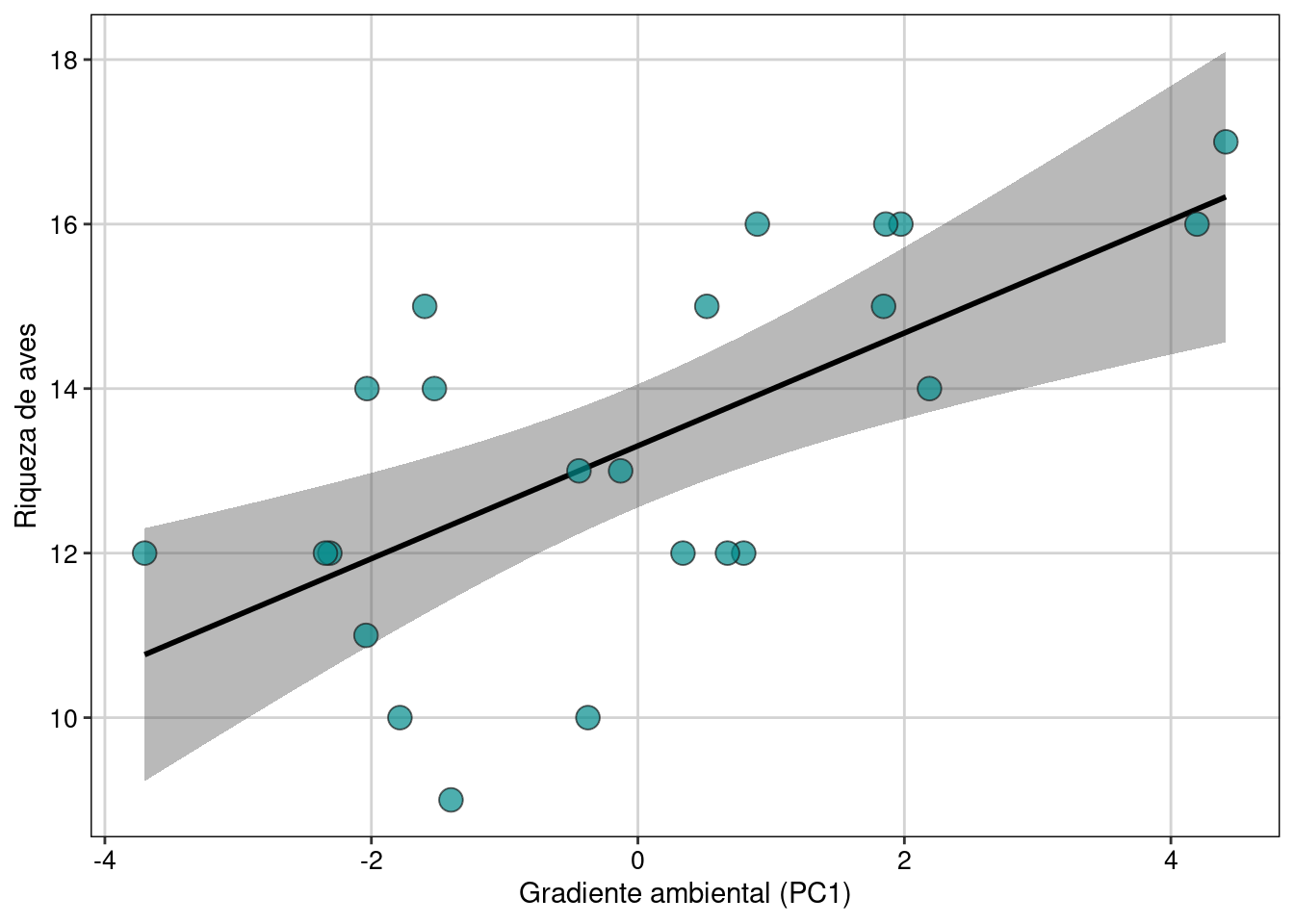
Figura 9.11: Modelo linear representando a relação entre Eixo 1 (gradiente chuva-temperatura) e a riqueza de espécies de aves.
Exemplo 2
É possível que os dados utilizados em seu estudo sejam mistos, ou seja, incluem tanto variáveis categóricas quanto contínuas. Como falado acima, nesses casos a análise indicada é a PCoA. Assim como na PCA, podemos extrair os escores da PCoA para utilizar em análises univariadas e multivariadas.
Pergunta
- Variáveis climáticas, vegetacionais e topográficas afetam a riqueza de ácaros?
Predições
- A densidade da vegetação e disponibilidade de água aumentam a riqueza de espécies de ácaros
Variáveis
- Preditoras: densidade de substrato e disponibilidade de água (contínuas), tipo de substrato (categórica com 7 níveis), densidade arbusto (ordinal com 3 níveis), e topografia (categórica com 2 níveis)
- Dependentes: riqueza de espécies de ácaros
O primeiro passo então é utilizar um método de distância apropriado para o seu conjunto de dados. Em nosso exemplo, utilizaremos a distância de Gower, que é usada para dados mistos (veja Capítulo 14).
## Matriz de distância
env.dist <- gowdis(mite.env)
## PCoA
env.mite.pco <- pcoa(env.dist, correction = "cailliez")
## Porcentagem de explicação do Eixo 1
100 * (env.mite.pco$values[, 1]/env.mite.pco$trace)[1]
#> [1] 61.49635
## Porcentagem de explicação dos Eixo 2
100 * (env.mite.pco$values[, 1]/env.mite.pco$trace)[2]
#> [1] 32.15486O próximo passo é exportar os escores para as análises a posteriori (Figura 9.12).
## Selecionar os dois primeiros eixos
pred.scores.mite <- env.mite.pco$vectors[, 1:2]
## Juntar com os dados da área para fazer a figura
mite.riqueza <- specnumber(mite)
pred.vars <- data.frame(riqueza = mite.riqueza, pred.scores.mite)
### Regressão múltipla
mod.mite <- lm(riqueza ~ Axis.1 + Axis.2, data = pred.vars)
par(mfrow = c(2, 2))
plot(mod.mite)
summary(mod.mite)
#>
#> Call:
#> lm(formula = riqueza ~ Axis.1 + Axis.2, data = pred.vars)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -10.6874 -2.3960 -0.1378 2.5032 8.6873
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 15.1143 0.4523 33.415 < 2e-16 ***
#> Axis.1 -11.4303 2.0013 -5.711 2.8e-07 ***
#> Axis.2 5.6832 2.7677 2.053 0.0439 *
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 3.784 on 67 degrees of freedom
#> Multiple R-squared: 0.3548, Adjusted R-squared: 0.3355
#> F-statistic: 18.42 on 2 and 67 DF, p-value: 4.225e-07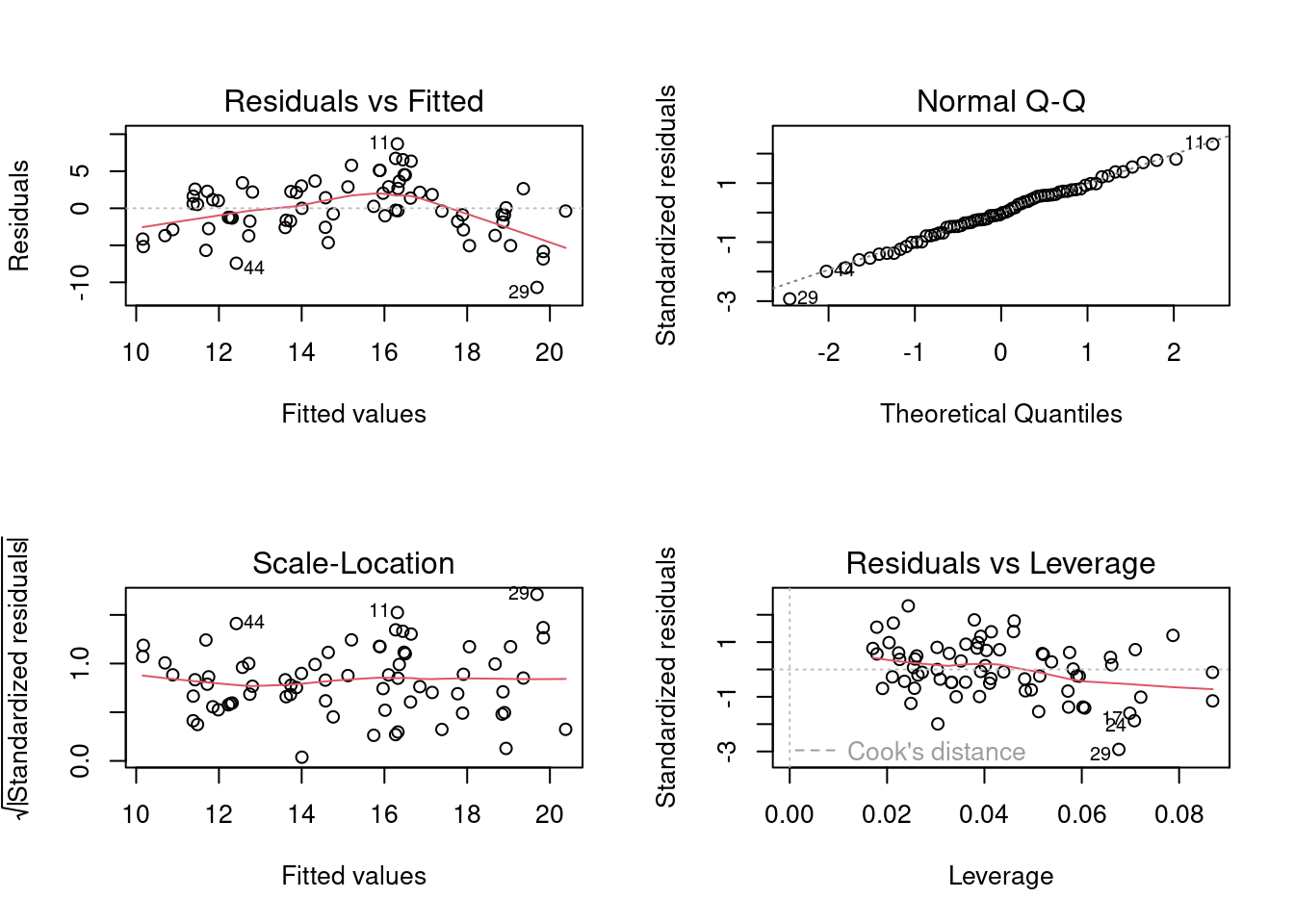
Figura 9.12: Diagnósticos dos modelo PCR para ácaros.
Finalmente, após interpretar os resultados do modelo, podemos fazer a figura com as variáveis (eixos) importantes (Figura 9.13).
g_acari_axi1 <- ggplot(pred.vars, aes(x = Axis.1, y = riqueza)) +
geom_smooth(method = lm, fill = "#525252", color = "black") +
geom_point(size = 4, shape = 21, alpha = 0.7, color = "#1a1a1a", fill="cyan4") +
labs(x = "Gradiente ambiental (PC1)", y = "Riqueza de ácaros") +
tema_livro()
g_acari_axi2 <- ggplot(pred.vars, aes(x = Axis.2, y = riqueza)) +
geom_smooth(method = lm, fill = "#525252", color = "black") +
geom_point(size = 4, shape = 21, alpha = 0.7, color = "#1a1a1a", fill = "darkorange") +
labs(x = "Gradiente ambiental (PC2)", y = "Riqueza de ácaros") +
tema_livro()
## Função para combinar os dois plots em uma única janela
grid.arrange(g_acari_axi1, g_acari_axi2, nrow = 1)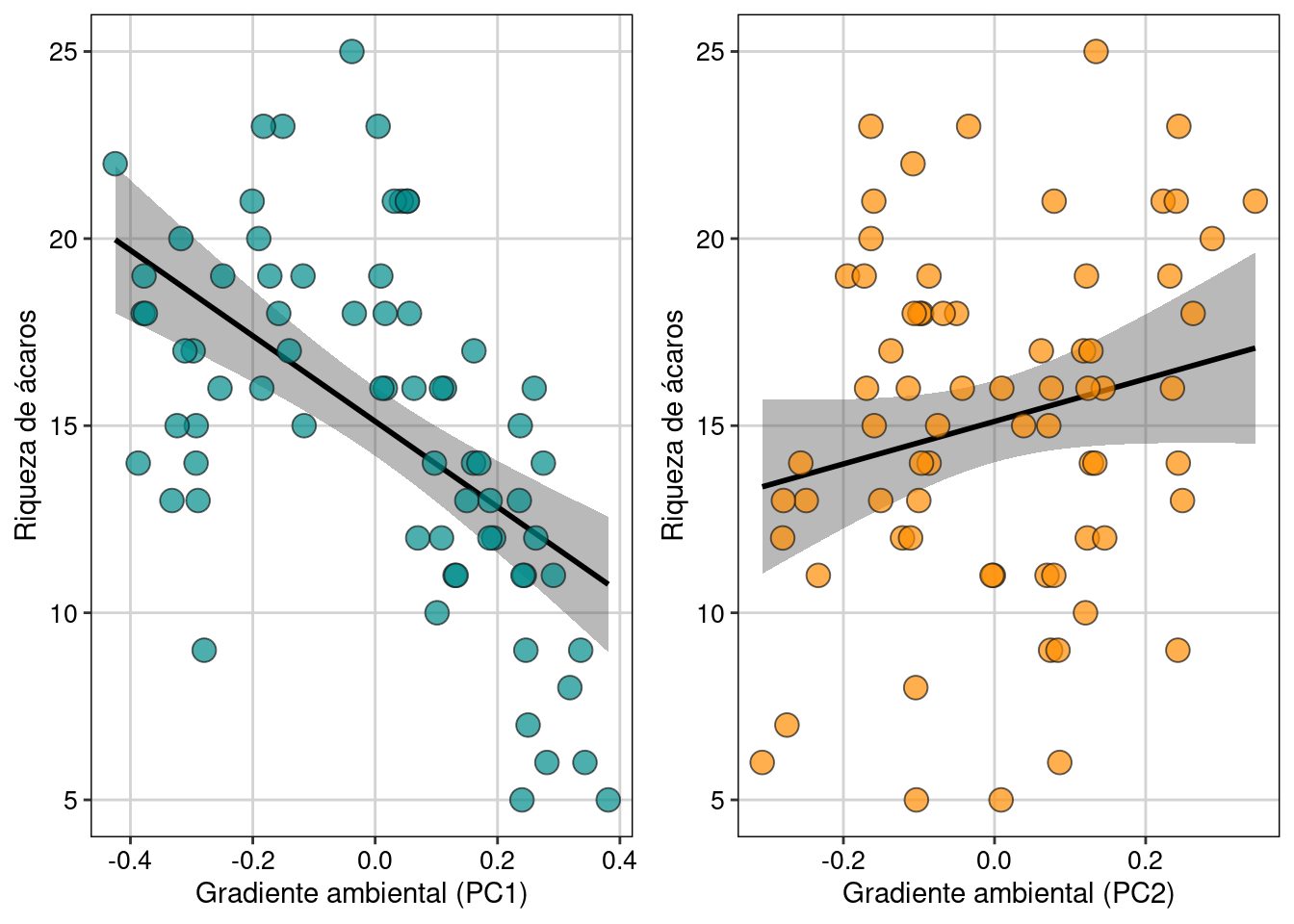
Figura 9.13: Modelo linear representando a relação entre Eixo 1 e Eixo 2 e a riqueza de espécies de ácaros.
9.5 Ordenação restrita
A ordenação restrita ou análise de gradiente direto, organiza os objetos de acordo com suas relações com outras variáveis (preditoras) coletadas nas mesmas unidades amostrais. O exemplo mais comum na ecologia é de investigar a relação entre diversas variáveis ambientais (matriz X) coletadas em n localidades e a abundância (ou presença ausência) de y espécies coletadas nas mesmas localidades (matrix Y). Com frequência, outros dados são utilizados como as coordenadas geográficas das unidades amostrais (matriz W), os atributos funcionais das espécies coletadas (matriz T) e a relação filogenética dessas espécies (matriz P). Diversos métodos são utilizados para combinar duas ou mais matrizes, mas neste capítulo iremos apresentar a Análise de Redundância (RDA), Análise de Redundância parcial (RDAp) e métodos espaciais para incluir a matriz W nas análises de gradiente direto.
9.5.1 Análise de Redundância (RDA)
A RDA é uma análise semelhante à regressão múltipla (Capítulo 7), mas que usa dados multivariados como variável dependente. As duas matrizes comuns, matriz X (n unidades amostrais e m variáveis) e matriz Y (n unidades amostrais e p descritores - geralmente, espécies). O primeiro passo da RDA é centralizar (assim como na PCA, exemplo acima) as matrizes X e Y. Após a centralização, realiza-se regressões lineares entre X e Y para obter os valores preditos de Y (ou seja, os valores de Y que representação uma combinação linear com X). O passo seguinte é realizar uma PCA dos valores preditos de Y. Este último procedimento gera os autovalores, autovetores e os eixos canônicos que correspondem às coordenadas dos objetos (unidades amostrais), variáveis preditoras e das variáveis resposta. A diferença da ordenação do valor de Y predito e da ordenação somente de Y (como na PCA implementada acima) é que a segunda mostra a posição prevista pela relação linear entre X e Y. Logo, essa é exatamente o motivo da ordenação ser conhecida como restrita, pois a variação em Y é restrita (linearmente) pela variação de X. Assim como na regressão múltipla, a estatística da RDA é representada pelo valor de R2 e F. O valor de R2 indica a força da relação linear entre X e Y e o valor do F representa o teste global de significância. Além disso, é possível testar a significância de cada um dos eixos da ordenação (e a presença de pelo menos um eixo significativo é pré-requisito para que exista a relação linear entre X e Y) e de cada uma das variáveis preditoras da matriz X.
Checklist
Variáveis preditoras: importante verificar se: i) a estrutura de correlação das variáveis ambientais, e a ii) presença de autocorrelação espacial
Composição de espécies como matriz Y: fundamental observar se os valores utilizados representam abundância ou presença-ausência e qual a necessidade de padronização (e.g., Hellinger)
Assim como em modelos de regressão linear simples e múltipla, os valores de R2 ajustado devem ser selecionados ao invés do valor de R2
Exemplo 1
Espécies de aves que ocorrem em localidades com diferentes altitudes.
Pergunta
- O clima e a altitude modificam a composição de espécies de aves?
Predições
- Diferenças climáticas (temperatura e chuva) e altitudinais alteram a composição de espécies de aves
Variáveis
- Preditoras: Temperatura e precipitação (contínuas) e altitude (categórica com três níveis)
- Dependente: composição de espécies de aves
Análises
## Passo 1: transformação de hellinger da matriz de espécies
# caso tenha dados de abundância.
species.hel <- decostand(x = species, method = "hellinger")
## Passo 2: selecionar variáveis importantes
# Para isso, é necessário remover a variável categórica.
env.contin <- env[, -8]
## Evite usar variáveis muito correlacionadas
sel.vars <- forward.sel(species.hel, env.contin)
#> Testing variable 1
#> Testing variable 2
#> Testing variable 3
#> Procedure stopped (alpha criteria): pvalue for variable 3 is 0.212000 (> 0.050000)
sel.vars$variables
#> [1] "rain.jul" "maxi.jul"
env.sel <- env[,sel.vars$variables]
## Passo 3: padronizar matriz ambiental (somente variáveis contínuas)
env.pad <- decostand(x = env.sel, method = "standardize")
## Matriz final com variáveis preditoras
env.pad.cat <- data.frame(env.pad, altitude = env$altitude)Depois de selecionar um subconjunto dos dados com o método Forward Selection e padronizá-los (média 0 e desvio padrão 1), o modelo da RDA é construído como modelos lineares (Figura 9.14). A Ordenação Multi-Escala (MSO) também é ajustada para analisar a autocorrelação espacial.
## RDA com dados selecionados e padronizados
rda.bird <- rda(species.hel ~ rain.jul + maxi.jul + altitude, data = env.pad.cat)
## Para interpretar, é necessário saber a significância dos eixos para representar a relação entre as variáveis preditoras e a composição de espécies
res.axis <- anova.cca(rda.bird, by = "axis")
res.axis
#> Permutation test for rda under reduced model
#> Forward tests for axes
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: rda(formula = species.hel ~ rain.jul + maxi.jul + altitude, data = env.pad.cat)
#> Df Variance F Pr(>F)
#> RDA1 1 0.045759 12.0225 0.001 ***
#> RDA2 1 0.009992 2.6252 0.061 .
#> RDA3 1 0.007518 1.9752 0.136
#> RDA4 1 0.003582 0.9410 0.470
#> Residual 18 0.068510
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Em seguida, é possível identificar quais são as variáveis que contribuem ou que mais contribuem para a variação na composição de espécies
res.var <- anova.cca(rda.bird, by = "term") ## Qual variável?
res.var
#> Permutation test for rda under reduced model
#> Terms added sequentially (first to last)
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: rda(formula = species.hel ~ rain.jul + maxi.jul + altitude, data = env.pad.cat)
#> Df Variance F Pr(>F)
#> rain.jul 1 0.036514 9.5936 0.001 ***
#> maxi.jul 1 0.011264 2.9596 0.016 *
#> altitude 2 0.019071 2.5053 0.011 *
#> Residual 18 0.068510
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Além disso, é possível obter o valor do R2 do modelo
r_quadr <- RsquareAdj(rda.bird)
r_quadr
#> $r.squared
#> [1] 0.4938685
#>
#> $adj.r.squared
#> [1] 0.3813949
## Ordenação multi-escala (MSO) para entender os resultados da ordenação em relação à distância geográfica
bird.rda <- mso(rda.bird, xy, grain = 1, permutations = 99)
msoplot(bird.rda)
#> Error variance of regression model underestimated by -2.7 percent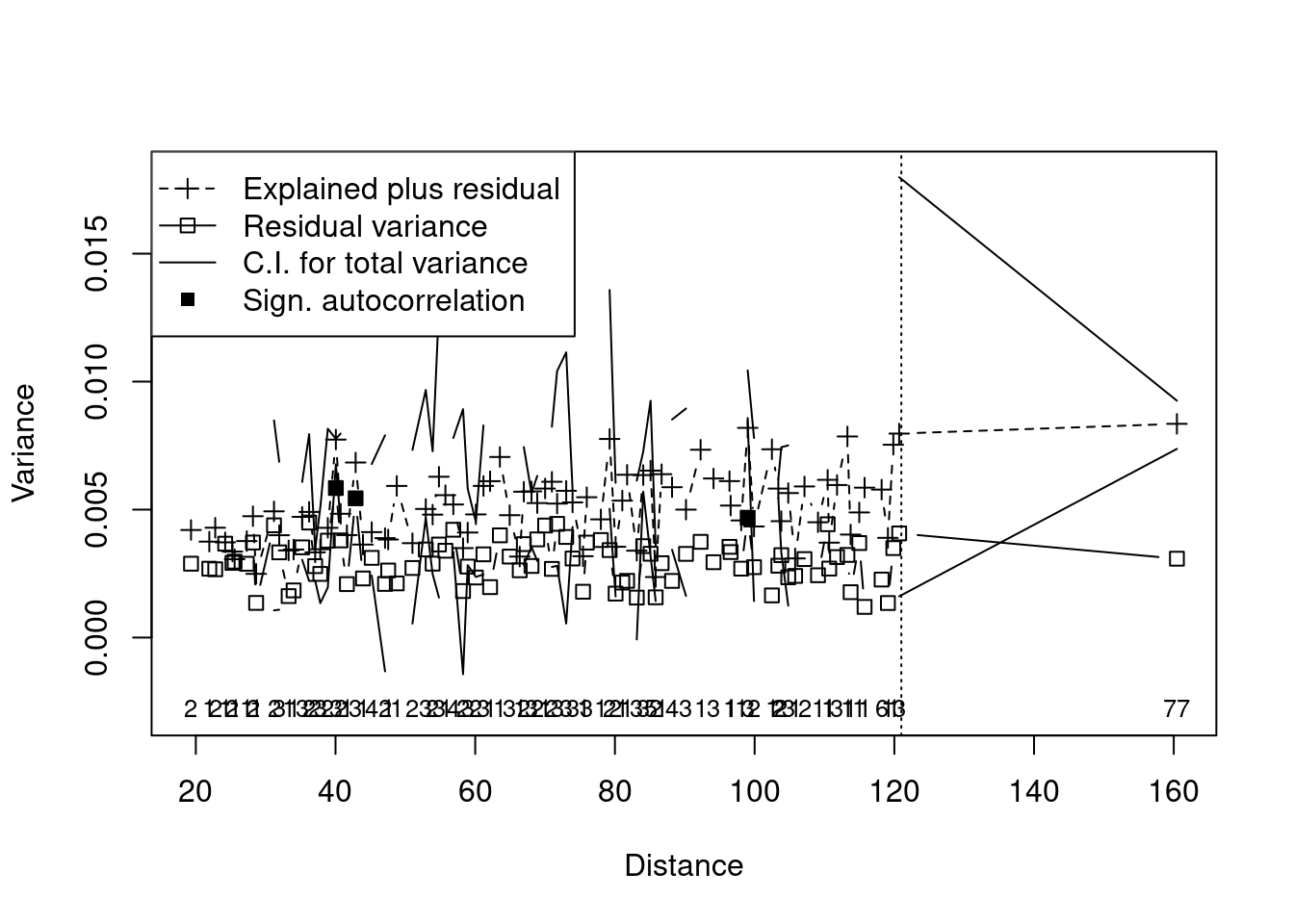
Figura 9.14: Ordenação multi-escala (MSO) para entender os resultados da ordenação em relação à distância geográfica.
Da mesma forma que nas ordenações irrestritas, podemos fazer um gráfico para visualizar as ordenações, mas agora esse gráfico é denominado “triplot”, pois possui os dados das duas ordenações (Figura 9.15).
## Triplot da RDA
ggord(rda.bird, ptslab = TRUE, size = 1, addsize = 3, repel = TRUE) +
geom_hline(yintercept = 0, linetype = 2) +
geom_vline(xintercept = 0, linetype = 2) +
tema_livro()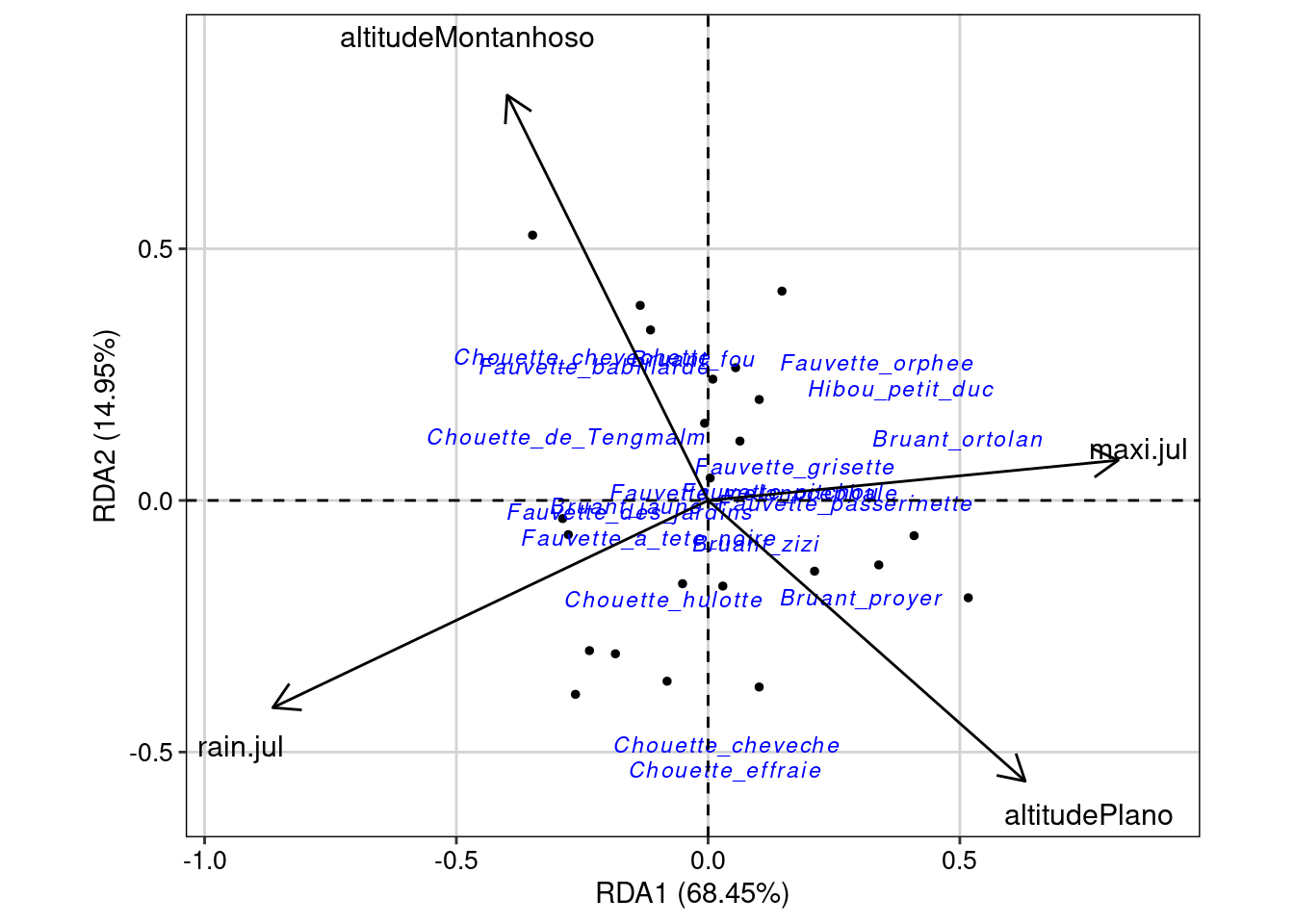
Figura 9.15: Triplot da RDA.
Interpretação dos resultados
Os objetos res.axis, res.var e r_quadr mostram, respectivamente, i) as dimensões (RDA1, RDA2, etc.) que possuem variação na composição de espécies, ii) as variáveis preditoras que explicam esta variação, e iii) o valor do R2 ajustado. Neste exemplo, podemos observar que somente a dimensão 1 (RDA1) representa uma variação significativa da composição de espécies (P = 0,001). As variáveis rain.jul, maxi.jul e altitude foram todas preditoras importantes da composição de espécies, mas rain.jul se destacada com maior valor de F. Além disso, o valor do R2 ajustado de 0.381 indica forte contribuição dessas variáveis preditoras. Porém, uma das limitações desta análise é não considerar que tanto espécies quanto variáveis preditoras podem estar estruturadas espacialmente. Como resultado, os resíduos das análises podem apresentar autocorrelação espacial que, por sua vez, aumenta o Erro do Tipo I (Legendre and Legendre 2012). A figura obtida com o código msoplot(bird.rda) demonstra que existe autocorrelação espacial em algumas distâncias da análise. Veja abaixo algumas alternativas para resíduos com autocorrelação espacial.
9.5.2 Análise de Redundância parcial (RDAp)
Um dos problemas da abordagem anterior é que tanto a composição de espécies como as variáveis ambientais estão estruturadas espacialmente. Talvez mais importantes, para que os valores de probabilidade da RDA sejam interpretados corretamente (e para evitar Erro do Tipo I), os resíduos do modelo não devem estar correlacionados espacialmente, como demonstrado com a análise MSO. Uma alternativa é incluir a matriz de dados espaciais (matrix W) como valor condicional dentro da RDA. Esta análise é conhecida como RDA parcial.
Porém, a obtenção dos dados espaciais da matriz W é mais complexo do que simplesmente incluir dados de localização geográfica (latitude e longitude), como feito em alguns modelos lineares (e.g., Generalized Least Squares - GLS Capítulos 7 e 10). Existem diversas ferramentas que descrevem e incorporam o componente espacial em métodos multidimensionais, mas os Mapas de Autovetores de Moran (MEM) são certamente os mais utilizados (Dray et al. 2012). A análise MEM consiste na ordenação (PCoA) de uma matriz truncada obtida através da localização geográfica das localidades utilizando distância euclidiana, matriz de conectividade e matriz espacial ponderada. Os autovalores obtidos no MEM são idênticos aos coeficientes de correlação espacial de Moran I. Um procedimento chave desta análise é a definição de um limiar de trucamento (do inglês truncate threshold). Este limiar é calculado a partir de uma “árvore de espaço mínimo” (Minimum Spanning Tree - MST) que conecta todos os pontos de coleta. Na prática, pontos com valores menores do que o limiar definido pela MST indicam que eles estão conectados e, assim possuem correlação positiva. Outro ponto importante desta análise é a obtenção da matriz espacial ponderada (Spatial Weighting Matrix - SWM). A seleção da matriz SWM é parte essencial do cálculo dos MEM e não deve ser feita arbitrariamente (Bauman, Drouet, Fortin, et al. 2018). Por este motivo, a análise recebe este nome (Legendre and Legendre 2012). Finalmente, o método produz autovetores que representam preditores espaciais que podem ser utilizados na RDA parcial (e em outras análises). É importante ressaltar que o critério de seleção do número de autovetores é bastante debatido na literatura e, para isso, sugerimos a leitura dos seguintes artigos: (Diniz-Filho et al. 2012; Bauman, Drouet, Fortin, et al. 2018; Bauman, Drouet, Dray, et al. 2018).
Então, o primeiro passo para realizar uma RDA parcial é de gerar os autovetores espaciais (MEMs).
## Dados
# Matriz padronizada de composição de espécies.
head(species.hel)[, 1:6]
#> Fauvette_orphee Fauvette_des_jardins Fauvette_a_tete_noire Fauvette_babillarde Fauvette_grisette Fauvette_pitchou
#> S01 0 0.3651484 0.3651484 0.2581989 0.2581989 0
#> S02 0 0.3333333 0.3333333 0.2357023 0.2357023 0
#> S03 0 0.3162278 0.3162278 0.3162278 0.2236068 0
#> S04 0 0.4200840 0.3429972 0.2425356 0.0000000 0
#> S05 0 0.3872983 0.3162278 0.2236068 0.3162278 0
#> S06 0 0.3779645 0.3779645 0.2672612 0.0000000 0
## Latitude e longitude
head(xy)
#> x y
#> S01 156 252
#> S02 141 217
#> S03 171 233
#> S04 178 215
#> S05 123 189
#> S06 154 195
## dados ambientais padronizados e altitude
head(env.pad.cat)
#> rain.jul maxi.jul altitude
#> S01 1.333646 0.1462557 Montanhoso
#> S02 1.468827 -0.6848206 Intermediário
#> S03 1.505694 -0.2099199 Montanhoso
#> S04 1.296778 -2.0699476 Montanhoso
#> S05 1.075572 -0.3682201 Plano
#> S06 1.100151 -0.6056705 Intermediário
## Passo 1: Gerar um arquivo LIST W: list binária de vizinhança
mat_knn <- knearneigh(as.matrix(xy), k = 2, longlat = FALSE)
mat_nb <- knn2nb(mat_knn, sym = TRUE)
mat_listw <- nb2listw(mat_nb, style = "W")
mat_listw
#> Characteristics of weights list object:
#> Neighbour list object:
#> Number of regions: 23
#> Number of nonzero links: 58
#> Percentage nonzero weights: 10.96408
#> Average number of links: 2.521739
#>
#> Weights style: W
#> Weights constants summary:
#> n nn S0 S1 S2
#> W 23 529 23 18.84444 96.01111
## Passo 2: Listar os métodos "candidatos" para obter a matriz SWM
MEM_mat <- scores.listw(mat_listw, MEM.autocor = "positive")
candidates <- listw.candidates(xy, nb = c("gab", "mst", "dnear"),
weights = c("binary", "flin"))
## Passo 3: Selecionar a melhor matriz SWM e executar o MEM
W_sel_mat <- listw.select(species.hel, candidates, MEM.autocor = "positive",
p.adjust = TRUE, method = "FWD")
#> Procedure stopped (alpha criteria): pvalue for variable 5 is 0.112000 (> 0.050000)
#> Procedure stopped (alpha criteria): pvalue for variable 3 is 0.059000 (> 0.050000)
#> Procedure stopped (alpha criteria): pvalue for variable 3 is 0.060000 (> 0.050000)
#> Procedure stopped (alpha criteria): pvalue for variable 4 is 0.157000 (> 0.050000)
## Passo 4: Matriz dos preditores espaciais escolhidos (MEMs)
spatial.pred <- as.data.frame(W_sel_mat$best$MEM.select)
## É necessário atribuir os nomes das linhas
rownames(spatial.pred) <- rownames(xy) Depois de gerar os valores dos autovetores espaciais (MEM), é possível executar a RDA parcial utilizando esses valores no argumento Conditional.
## Combinar variáveis ambientais e espaciais em um único data.frame
pred.vars <- data.frame(env.pad.cat, spatial.pred)
## RDA parcial
rda.p <- rda(species.hel ~
rain.jul + maxi.jul + altitude + # Preditores ambientais
Condition(MEM1 + MEM2 + MEM4 + MEM5), # Preditores espaciais
data = pred.vars)
## Interpretação
# Para interpretar, é necessário saber a significância dos eixos para representar a relação entre as variáveis preditoras e a composição de espécies.
res.p.axis <- anova.cca(rda.p, by = "axis")
res.p.axis
#> Permutation test for rda under reduced model
#> Forward tests for axes
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: rda(formula = species.hel ~ rain.jul + maxi.jul + altitude + Condition(MEM1 + MEM2 + MEM4 + MEM5), data = pred.vars)
#> Df Variance F Pr(>F)
#> RDA1 1 0.008471 2.1376 0.316
#> RDA2 1 0.004830 1.2189 0.779
#> RDA3 1 0.003240 0.8176 0.890
#> RDA4 1 0.001891 0.4773 0.895
#> Residual 14 0.055477
## Contribuição
# Em seguida, é possível identificar quais são as variáveis que contribuem ou que mais contribuem para a variação na composição de espécies.
res.p.var <- anova.cca(rda.p, by = "term") ## Qual variável?
res.p.var
#> Permutation test for rda under reduced model
#> Terms added sequentially (first to last)
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: rda(formula = species.hel ~ rain.jul + maxi.jul + altitude + Condition(MEM1 + MEM2 + MEM4 + MEM5), data = pred.vars)
#> Df Variance F Pr(>F)
#> rain.jul 1 0.004406 1.1119 0.349
#> maxi.jul 1 0.004446 1.1220 0.338
#> altitude 2 0.009579 1.2087 0.241
#> Residual 14 0.055477
RsquareAdj(rda.p)
#> $r.squared
#> [1] 0.1361661
#>
#> $adj.r.squared
#> [1] 0.02330319Se você comparar os resultados do objeto res.p.var (RDA parcial) com res.var (RDA simples) é possível perceber como a estrutura espacial nos resíduos aumenta a probabilidade de cometer Erro do Tipo I. O modelo da RDA parcial mostra que não existem qualquer efeito direto das variáveis ambientais sobre a composição de espécies (conclusão com a RDA simples). Na verdade, tanto a composição de espécies quanto as variáveis climáticas estão fortemente estruturadas no espaço, como demonstramos a seguir.
## Padrão espacial na composição de espécies
pca.comp <- dudi.pca(species.hel, scale = FALSE, scannf = FALSE)
moran.comp <- moran.mc(pca.comp$li[, 1], mat_listw, 999)
## Padrão espacial das variáveis ambientais
env$altitude <- as.factor(env$altitude)
ca.env <- dudi.hillsmith(env, scannf = FALSE)
moran.env <- moran.mc(ca.env$li[, 1], mat_listw, 999)
## Estrutura espacial na composição de espécies?
moran.comp
#>
#> Monte-Carlo simulation of Moran I
#>
#> data: pca.comp$li[, 1]
#> weights: mat_listw
#> number of simulations + 1: 1000
#>
#> statistic = 0.62815, observed rank = 1000, p-value = 0.001
#> alternative hypothesis: greater
## Estrutura espacial na variação ambiental?
moran.env
#>
#> Monte-Carlo simulation of Moran I
#>
#> data: ca.env$li[, 1]
#> weights: mat_listw
#> number of simulations + 1: 1000
#>
#> statistic = 0.72714, observed rank = 1000, p-value = 0.001
#> alternative hypothesis: greaterComo resultado, é possível que a variação ambiental espacialmente estruturada seja o principal efeito sobre a composição de espécies. Uma maneira de visualizar a contribuição relativa de diferentes matrizes (ambiental e espacial, por exemplo) é utilizar o método de partição de variância. O resultado deste modelo indica que, de fato, não existe efeito direto das variáveis ambientais e sim do componente representado pela autocorrelação espacial dessas variáveis (Figura 9.16).
## Triplot da RDA
# Partição de variância.
pv.birds <- varpart(species.hel, env.pad.cat, spatial.pred)
plot(pv.birds, cutoff = -Inf)
mtext("Diagrama de Venn: partição de variância")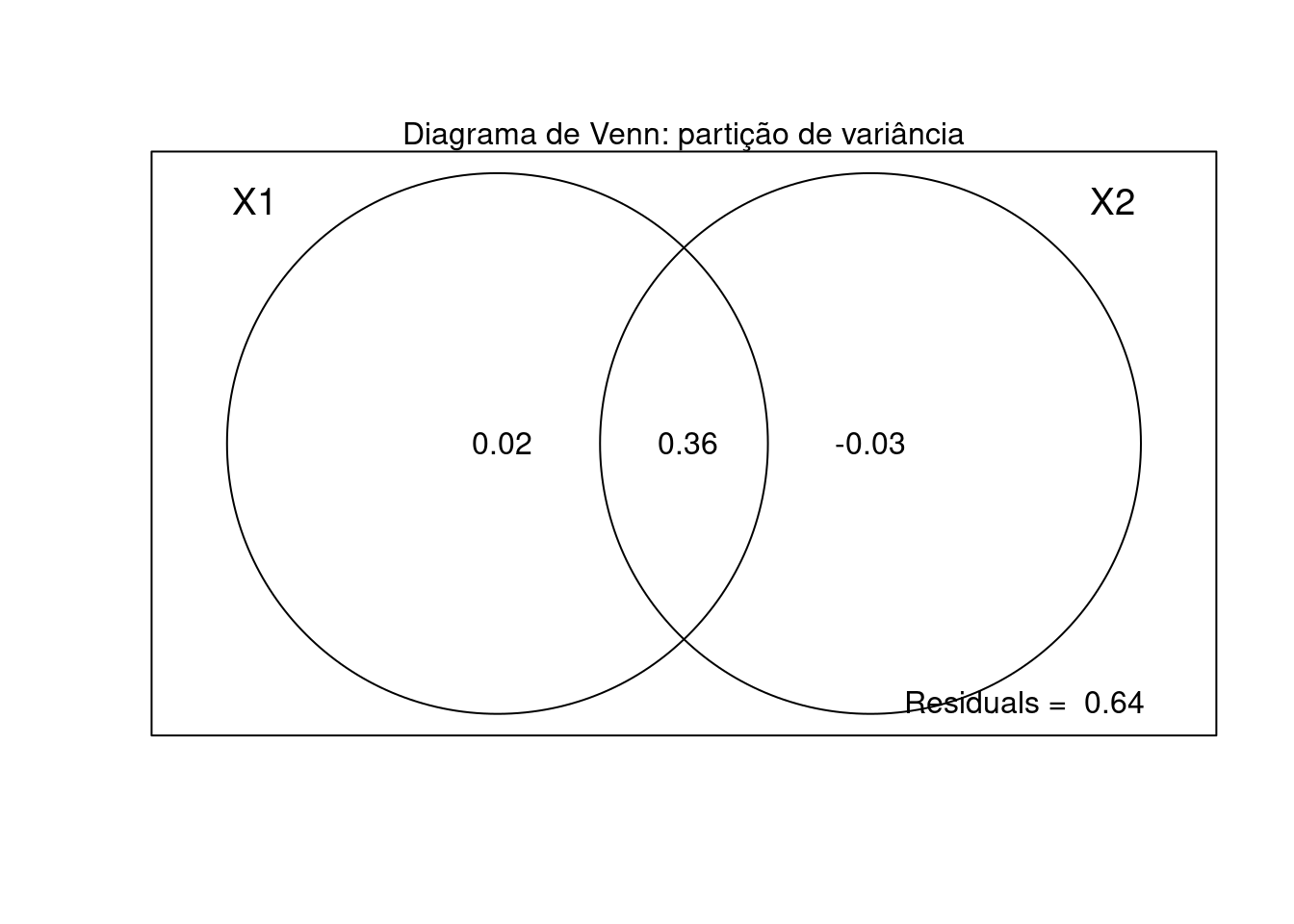
Figura 9.16: Diagrama de Venn mostrando a partição de variância da RDA.
9.5.3 Análise de Redundância baseada em distância (db-RDA)
Acima, apresentamos a análise RDA que permite comparar, por exemplo, se variáveis ambientais determinam a variação na composição de espécies. A RDA utiliza os dados brutos de composição de espécies e é baseada em uma PCA (i.e., requer distância euclidiana). Porém, em algumas situações é necessário utilizar outras medidas de distância tais como Bray-Curtis ou Gower. Esta análise é bastante útil também quando a matriz resposta já é uma matriz de distância, tais como as que são geradas por decomposição da diversidade beta. Neste caso, Legendre & Anderson (1999) propuseram a análise db-RDA (RDA baseada em distância). O primeiro passo da análise é gerar uma matriz de distância a partir da matriz bruta (e.g., composição de espécies). Depois, a técnica executa uma PCoA (corrigindo potenciais autovetores com autovalores negativos; ver discussão acima) para comparar com os termos do modelo (matriz X, como na RDA).
Para exemplificar como esta análise pode ser implementada no R, vamos usar o mesmo exemplo demonstrado na análise RDA (ver acima). Porém, vamos fazer um ajuste sutil na pergunta “o clima e a altitude modificam a dissimilaridade (diversidade beta) de espécies de aves?”. Veja que neste caso, estamos perguntando diretamente sobre uma medida de diversidade beta, que será calculada com o método Bray-Curtis. As variáveis preditoras serão as mesmas obtidas no exemplo da RDA: env.pad.cat.
Análise
## Passo 1: transformação de hellinger da matriz de espécies
# caso tenha dados de abundância.
species.hel <- decostand(species, "hellinger")
## Passo 2: gerar matriz de distância (Diversidade beta: Bray-Curtis)
dbeta <- vegdist(species.hel, "bray")
## Passo 2: dbRDA
dbrda.bird <- capscale (dbeta~rain.jul+maxi.jul+altitude, data=env.pad.cat)
# Para interpretar, é necessário saber a significância dos eixos para representar a relação entre as variáveis preditoras e a composição de espécies
db.res.axis <- anova.cca(dbrda.bird, by = "axis")
db.res.axis
#> Permutation test for capscale under reduced model
#> Forward tests for axes
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: capscale(formula = dbeta ~ rain.jul + maxi.jul + altitude, data = env.pad.cat)
#> Df SumOfSqs F Pr(>F)
#> CAP1 1 0.274186 16.9355 0.001 ***
#> CAP2 1 0.044965 2.7773 0.110
#> CAP3 1 0.018141 1.1205 0.656
#> CAP4 1 0.009500 0.5868 0.788
#> Residual 18 0.291420
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Em seguida, é possível identificar quais são as variáveis que contribuem ou que mais contribuem para a variação na composição de espécies
db.res.var <- anova.cca(dbrda.bird, by = "term") ## Qual variável?
db.res.var
#> Permutation test for capscale under reduced model
#> Terms added sequentially (first to last)
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: capscale(formula = dbeta ~ rain.jul + maxi.jul + altitude, data = env.pad.cat)
#> Df SumOfSqs F Pr(>F)
#> rain.jul 1 0.209981 12.9697 0.001 ***
#> maxi.jul 1 0.041846 2.5847 0.070 .
#> altitude 2 0.094966 2.9328 0.012 *
#> Residual 18 0.291420
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Além disso, é possível obter o valor do R2 do modelo
db_r_quadr <- RsquareAdj(dbrda.bird)
db_r_quadr
#> $r.squared
#> [1] 0.6116758
#>
#> $adj.r.squared
#> [1] 0.5253816Interpretação dos resultados
Assim como apresentado na RDA, os resultados obtidos em db.res.var sugerem que as variáveis rain.jul, maxi.jul e altitude afetam a diversidade beta de aves. O valor do R2 ajustado (0.495) sugere forte relação entre o gradiente ambiental e a diversidade beta. A comparação entre o valor do db_r_quadr e r_quadr indica que a db-RDA teve melhor ajuste para comparar o mesmo conjunto de dados.
9.6 PERMANOVA
A PERMANOVA é uma sigla, em inglês, de Permutational Multivariate Analysis of Variance, análise proposta por Marti Anderson (M. J. Anderson 2001). A PERMANOVA é usada para testar hipóteses multivariadas que comparam a abundância de diferentes espécies em resposta a diferentes tratamentos ou gradientes ambientais. Essa análise foi desenvolvida como forma de solucionar algumas limitações da tradicional ANOVA multivariada (MANOVA). Em especial, o pressuposto da MANOVA de distribuição normal multivariada é raramente encontrado em dados ecológicos.
O primeiro passo da PERMANOVA é selecionar uma medida de distância apropriada aos dados e, além disso, verificar a necessidade de padronização ou transformação dos dados. Em seguida, as distâncias são comparadas entre os grupos de interesse (por exemplo, tratamento versus controle) usando a estatística F de maneira muito parecida com uma ANOVA (Capítulo 7), chamada de pseudo-F:
\[F_pseudo = (SSa / SSr)*[(N-g) / (g-1)]\]
Nessa equação
- SSa representa a soma dos quadrados entre grupos
- SSr a soma de quadrados dentro do grupo (residual)
- N o número de unidades amostrais
- g os grupos (ou níveis da variável categórica)
Esta fórmula do pseudo-F é específica para desenho experimental com um fator. Outros desenhos mais complexos são apresentados em Anderson (2001, 2017). O cálculo do valor de probabilidade é realizado por métodos de permutação que são discutidos em Anderson & Ter Braak (2003).
Exemplo 1
Espécies de aves que ocorrem em localidades com diferentes altitudes.
Pergunta
- O clima e a altitude modificam a composição de espécies de aves?
Predições
- Diferenças climáticas (temperatura e chuva) e altitudinais alteram a composição de espécies de aves
Variáveis
- Preditoras: Temperatura e chuva (contínuas) e altitude (categórica com três níveis)
- Dependente: composição de espécies de aves
## Composição de espécies padronizar com método de Hellinger
species.hel <- decostand(x = species, method = "hellinger")
## Matriz de distância com método Bray-Curtis
sps.dis <- vegdist(x = species.hel, method = "bray")Para reduzir o número de variáveis no modelo, você pode considerar duas abordagens. A primeira, e mais importante delas, é manter somente variáveis preditoras que você tenha razão biológica para mantê-la e, além disso, que esteja relacionada com suas hipóteses. Assim, uma vez que você já removeu variáveis que não possuem relevância biológica, você deve usar diferentes métodos para remover as variáveis muito correlacionadas (forward selection, Variance Inflation Factor (VIF), entre outros). Neste exemplo, vamos simplesmente fazer uma correlação múltipla e remover as variáveis com correlação maior do que 0.9 ou -0.9. A função ggpairs() mostra um gráfico bem didático para representar a relação entre todas as variáveis e o valor (r) desta correlação (mais em Capítulo 7) (Figura 9.17).
## Verifica correlação entre as variáveis
ggpairs(env) +
tema_livro()
## Após verificar a estrutura de correlação, vamos manter somente três variáveis
env2 <- env[, c("mini.jan", "rain.tot", "altitude")]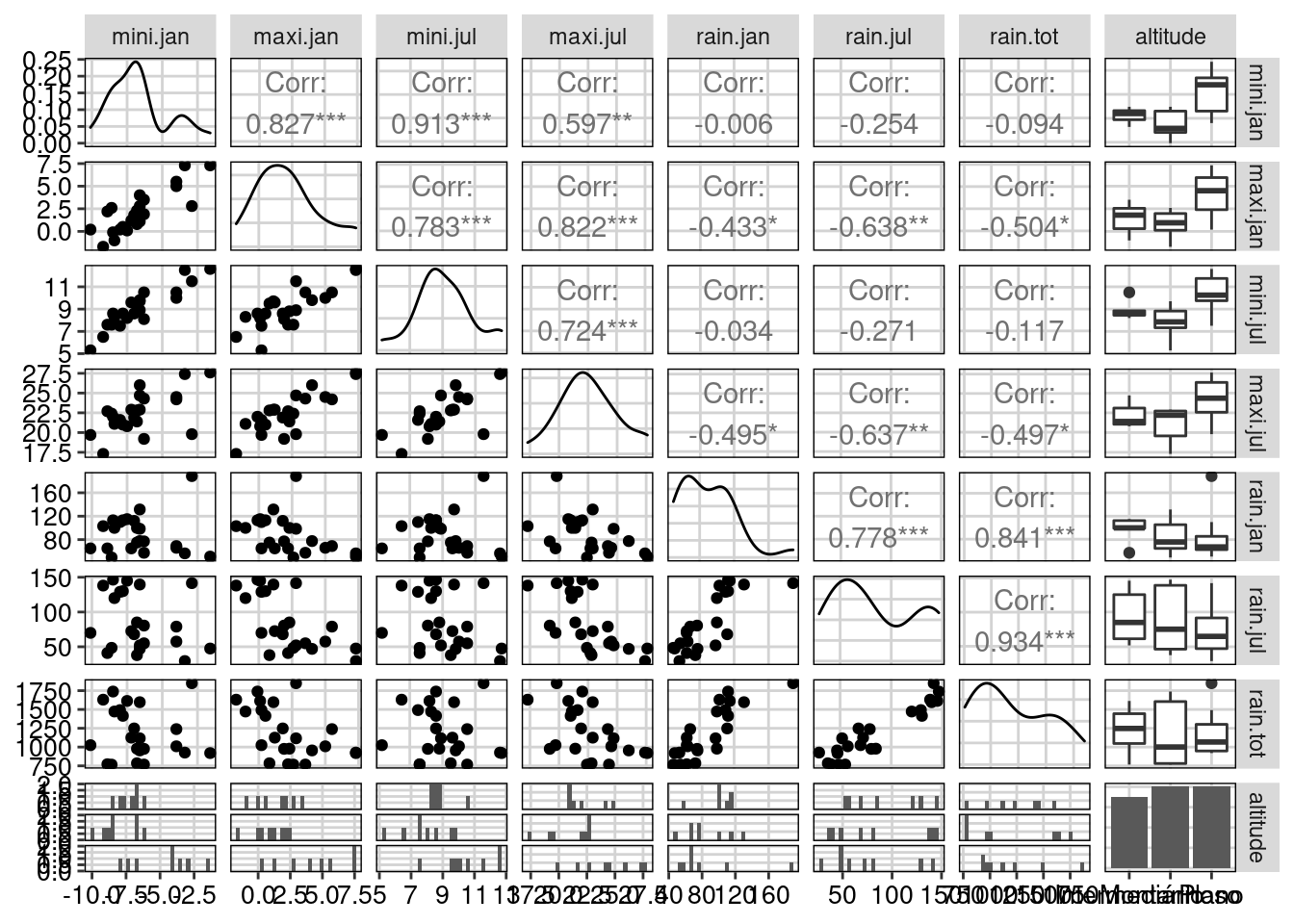
Figura 9.17: Correlograma mostrando a correlação entre as variáveis.
Após selecionar as variáveis do modelo, vamos executar a PERMANOVA e entender as principais etapas para interpretar corretamente o teste. A função adonis() do pacote vegan é uma boa opção. Porém, é importante referir o programa PRIMER e PERMANOVA+ como ótima opção para implementar a PERMANOVA e ter maior controle em desenhos complexos (M. J. Anderson, Gorley, and Clarke 2008). Assim como nos modelos lineares apresentados no Capítulo 7, os argumentos seguem o mesmo formato, com variável dependente separada por um “~” das variáveis preditoras. Porém, alguns autores demonstraram que a PERMANOVA (assim como Mantel e ANOSIM) não pode identificar se diferenças significativas do teste (usando a estatística pseudo-F) devem-se à diferenças no posição, na dispersão ou ambos. Ou seja, ao comparar grupos não é possível identificar se existe mudanças de composição (posição) ou se a variação da composição de espécies dentro de um grupo (dispersão) é maior do que a variação dentro do outro grupo (M. J. Anderson and Walsh 2013). Para solucionar este problema, é possível combinar a PERMANOVA com a análise PERMDISP (ou BETADISPER, como chamado no pacote vegan implementado através da função betadisper()). Esta análise permite comparar se existe heterogeneidade nas variâncias entre grupos. Deste modo, com a presença de heterogeneidade de variâncias (valor do BETADISPER significativo), é possível saber que as diferenças entre os grupos ocorrem principalmente por diferenças na dispersão e não, necessariamente, de posição. Mais detalhes sobre a relevância de combinar essas duas análises estão disponíveis em Anderson & Walsh (2013).
## PERMANOVA
perm.aves <- adonis2(sps.dis ~ mini.jan + rain.tot + altitude, data = env2)
perm.aves ### Diferenças entre os tratamentos?
#> Permutation test for adonis under reduced model
#> Terms added sequentially (first to last)
#> Permutation: free
#> Number of permutations: 999
#>
#> adonis2(formula = sps.dis ~ mini.jan + rain.tot + altitude, data = env2)
#> Df SumOfSqs R2 F Pr(>F)
#> mini.jan 1 0.09069 0.15997 6.3307 0.001 ***
#> rain.tot 1 0.12910 0.22771 9.0118 0.001 ***
#> altitude 2 0.08929 0.15749 3.1163 0.011 *
#> Residual 18 0.25787 0.45483
#> Total 22 0.56695 1.00000
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## BETADISPER
betad.aves <- betadisper(sps.dis, env2$altitude)
permutest(betad.aves)
#>
#> Permutation test for homogeneity of multivariate dispersions
#> Permutation: free
#> Number of permutations: 999
#>
#> Response: Distances
#> Df Sum Sq Mean Sq F N.Perm Pr(>F)
#> Groups 2 0.0042643 0.0021322 1.4672 999 0.265
#> Residuals 20 0.0290636 0.0014532Em nosso exemplo, a temperatura, precipitação e altitude afetaram a variação na composição de espécies. Porém, para identificar se as diferenças de composição entre os níveis da variável altitude, é necessário interpretar os resultados da análise BETADISPER. O código permutest(betad.aves) mostra que o valor de probabilidade da análise foi de 0.253, ou seja, a hipótese nula de que a variância entre grupos é homogênea é aceita. Assim, não existe diferenças na dispersão entre grupos, sugerindo que a diferença encontrada na PERMANOVA (objeto perm.aves) se deve, em parte, à mudança na composição de espécies de aves entre diferentes altitudes (R2 = 0.135). Além disso, a precipitação (R2 = 0.183) e temperatura (R2 = 0.127) foram fatores importantes na variação da composição de espécies.
Como falado anteriormente, as análises de ordenação irrestritas (PCA, PCoA, nMDS) são utilizadas para explorar dados. Uma maneira poderosa de usá-las é combinando com análises que testam hipóteses, como PERMANOVA e RDA. A literatura ecológica tem usado a Análise de Escalonamento não-Métrico (non-Metric Multidimensional Scaling - nMDS) combinado com análises multidimensionais de variância (como a PERMANOVA) para visualização da similaridade na composição de espécies dentro e entre grupos. A seguir, implementamos o nMDS na matriz de composição de espécies de ácaros (Figura 9.18).
## Matriz de distância representando a variação na composição de espécies (método Bray-Curtis)
as.matrix(sps.dis)[1:6, 1:6]
#> S01 S02 S03 S04 S05 S06
#> S01 0.0000000 0.15133734 0.16720405 0.2559122 0.2559882 0.2588892
#> S02 0.1513373 0.00000000 0.04114702 0.1190172 0.1289682 0.1391056
#> S03 0.1672040 0.04114702 0.00000000 0.1420233 0.1358127 0.1410867
#> S04 0.2559122 0.11901720 0.14202325 0.0000000 0.1140283 0.1199803
#> S05 0.2559882 0.12896823 0.13581271 0.1140283 0.0000000 0.2129054
#> S06 0.2588892 0.13910558 0.14108668 0.1199803 0.2129054 0.0000000
## É preciso calcular uma primeira "melhor" solução do nMDS
sol1 <- metaMDS(sps.dis)
#> Run 0 stress 0.1344042
#> Run 1 stress 0.3825954
#> Run 2 stress 0.1272417
#> ... New best solution
#> ... Procrustes: rmse 0.07890815 max resid 0.3526073
#> Run 3 stress 0.1344042
#> Run 4 stress 0.1338432
#> Run 5 stress 0.1626783
#> Run 6 stress 0.1336481
#> Run 7 stress 0.1272417
#> ... Procrustes: rmse 6.723274e-06 max resid 1.889203e-05
#> ... Similar to previous best
#> Run 8 stress 0.1338432
#> Run 9 stress 0.1378506
#> Run 10 stress 0.1272418
#> ... Procrustes: rmse 0.0001085155 max resid 0.0004162969
#> ... Similar to previous best
#> Run 11 stress 0.1272418
#> ... Procrustes: rmse 4.197901e-05 max resid 0.000160606
#> ... Similar to previous best
#> Run 12 stress 0.1378506
#> Run 13 stress 0.1272418
#> ... Procrustes: rmse 5.310796e-05 max resid 0.0001988503
#> ... Similar to previous best
#> Run 14 stress 0.1580523
#> Run 15 stress 0.1344042
#> Run 16 stress 0.1272418
#> ... Procrustes: rmse 2.586759e-05 max resid 9.827497e-05
#> ... Similar to previous best
#> Run 17 stress 0.1584787
#> Run 18 stress 0.1344042
#> Run 19 stress 0.1344042
#> Run 20 stress 0.1344042
#> *** Solution reached
## Melhor solução
# Depois, executar a mesma função, mas utilizando uma "melhor solução inicial" para evitar resultdos subótimos no nMDS .
nmds.beta <- metaMDS(sps.dis, previous.best = sol1)
#> Starting from 2-dimensional configuration
#> Run 0 stress 0.1272417
#> Run 1 stress 0.1272418
#> ... Procrustes: rmse 2.188819e-05 max resid 7.340362e-05
#> ... Similar to previous best
#> Run 2 stress 0.1338432
#> Run 3 stress 0.1584788
#> Run 4 stress 0.1344043
#> Run 5 stress 0.1338433
#> Run 6 stress 0.1336481
#> Run 7 stress 0.1344042
#> Run 8 stress 0.1338432
#> Run 9 stress 0.1272418
#> ... Procrustes: rmse 2.708248e-05 max resid 0.0001008894
#> ... Similar to previous best
#> Run 10 stress 0.1336481
#> Run 11 stress 0.1344042
#> Run 12 stress 0.3798204
#> Run 13 stress 0.1336481
#> Run 14 stress 0.1336481
#> Run 15 stress 0.1344042
#> Run 16 stress 0.1336481
#> Run 17 stress 0.1338432
#> Run 18 stress 0.1272418
#> ... Procrustes: rmse 2.303898e-05 max resid 8.758403e-05
#> ... Similar to previous best
#> Run 19 stress 0.1344042
#> Run 20 stress 0.1378506
#> *** Solution reached
## Stress
# O stress é o valor mais importante para interpretar a qualidade da ordenação.
nmds.beta$stress # valor ideal entre 0 e 0.2
#> [1] 0.1272417
## Exportar os valores para fazer gráfico
dat.graf <- data.frame(nmds.beta$points, altitude = env2$altitude)
## Definir os grupos ("HULL") para serem categorizados no gráfico
grp.mon <- dat.graf[dat.graf$altitude == "Montanhoso", ][chull(dat.graf[dat.graf$altitude == "Montanhoso", c("MDS1", "MDS2")]), ]
grp.int <- dat.graf[dat.graf$altitude == "Intermediário", ][chull(dat.graf[dat.graf$altitude == "Intermediário", c("MDS1", "MDS2")]), ]
grp.pla <- dat.graf[dat.graf$altitude == "Plano", ][chull(dat.graf[dat.graf$altitude == "Plano", c("MDS1", "MDS2")]), ]
## Combinar dados dos grupos para cada Convex Hull
hull.data <- rbind(grp.mon, grp.int, grp.pla)
head(hull.data)
#> MDS1 MDS2 altitude
#> S04 -0.10578586 -0.10682766 Montanhoso
#> S01 -0.25332406 0.04199004 Montanhoso
#> S11 -0.12504415 0.14477005 Montanhoso
#> S15 0.09166059 0.09857114 Montanhoso
#> S18 0.01968127 -0.12417579 Intermediário
#> S06 -0.16053825 -0.08924030 Intermediário
## Gráfico
ggplot(dat.graf, aes(x = MDS1, y = MDS2, color = altitude, shape = altitude)) +
geom_point(size = 4, alpha = 0.7) +
geom_polygon(data = hull.data, aes(fill = altitude, group = altitude), alpha = 0.3) +
scale_color_manual(values = c("darkorange", "darkorchid", "cyan4")) +
scale_fill_manual(values = c("darkorange", "darkorchid", "cyan4")) +
labs(x = "NMDS1", y = "NMDS2") +
tema_livro()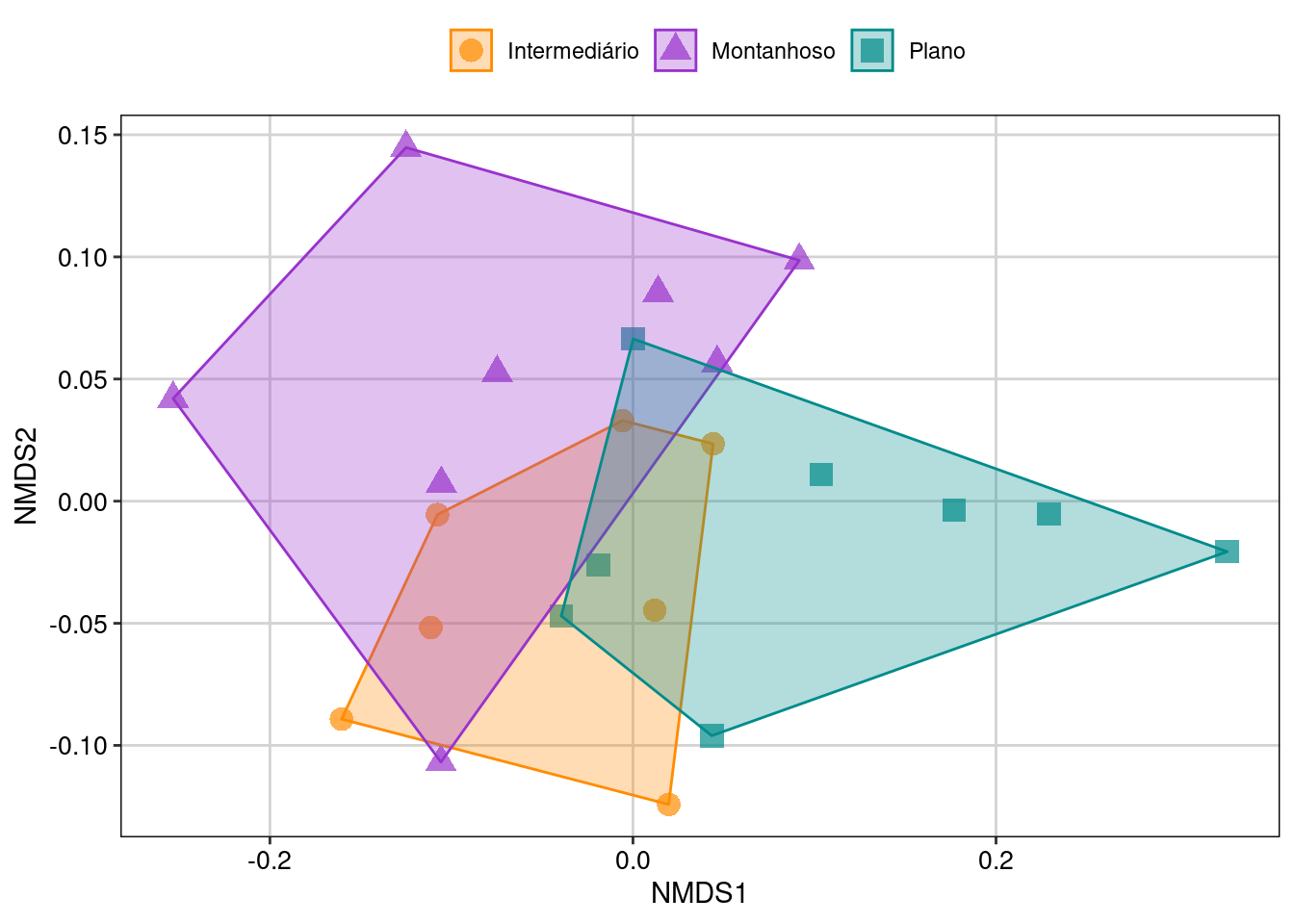
Figura 9.18: Biplot mostrando o resultado do nMDS.
9.7 Mantel e Mantel parcial
O teste de Mantel se aplica quando temos duas ou mais matrizes de distância (triangulares). Em estudos ecológicos, essas matrizes normalmente descrevem dados de distância ou (dis)similaridade na composição de espécies, distância geográfica, e similaridade ambiental. Mas este teste também é amplamente aplicado na área de genética de paisagem para testar hipóteses sobre como a composição genética de uma população varia em função do ambiente e/ou espaço geográfico (Legendre and Fortin 2010). O teste nada mais é do que uma generalização do coeficiente de correlação de Pearson (Capítulo 7) para lidar com matrizes de distância. Como essas matrizes descrevem a relação entre vários pares de locais, temos a repetição do mesmo local em outros pares. Neste caso é preciso um procedimento semelhante ao de correção para múltiplos testes.
Já o Mantel parcial pretende testar a correlação entre duas matrizes controlando para o efeito de uma terceira. Por exemplo, testar a associação entre a dissimilaridade na composição de espécies e dissimilaridade ambiental, controlando para a distância geográfica entre os locais. Isso nos permite levar em conta a possível autocorrelação espacial nas variáveis ambientais, ou seja, estaríamos testando de fato o efeito da dissimilaridade ambiental “pura” na dissimilaridade na composição de espécies, evitando o efeito do espaço em si. Portanto, note que sempre estamos raciocinando em termos de (dis)similaridade e não dos dados brutos em si, seja composição de espécies ou variáveis ambientais. É importante ter isto em mente na hora de interpretar os resultados.
Exemplo 1
Neste exemplo, vamos utilizar um conjunto de dados que contém girinos de espécies de anfíbios anuros coletados em 14 poças d’água e os respectivos dados de variáveis ambientais destas mesmas poças (Provete et al. 2014).
Pergunta
- Existe correlação entre a dissimilaridade na composição de espécies de girinos e a dissimilaridade ambiental?
Predições
- Assumindo que processos baseados no nicho sejam predominantes, quanto mais diferentes as poças forem maior será a diferença na composição de espécies
Variáveis
- Variáveis: a matriz de distância (Bray-Curtis) da composição das espécies e outra matriz de distância (Euclideana) das variáveis ambientais
Análises
Aqui vamos utilizar além do conjunto de dados bocaina já conhecido, outras duas matrizes disponíveis no pacote ecodados: bocaina.xy e bocaina.env, que contêm as coordenadas geográficas e variáveis ambientais das poças, respectivamente.
## Dados
head(bocaina.env)
#> pH tur DO temp veg dep canopy conduc hydro area
#> PP3 7.07 0.66 2.26 18.93 30 0.35 30.3 0.0100 per 139
#> PP4 6.85 0.33 2.78 20.53 0 0.33 32.1 0.0100 per 223
#> AP1 6.64 0.40 4.09 15.26 5 3.50 42.0 0.0105 per 681
#> AP2 6.13 0.80 3.47 15.40 70 2.50 82.0 0.0300 per 187
#> PP1 5.80 0.75 3.22 16.75 70 0.70 91.4 0.0100 per 83
#> PP2 5.32 4.00 2.10 15.90 95 0.27 75.3 0.0100 per 108
head(bocaina.xy)
#> Long Lat
#> PT5 -44.6239 -22.7243
#> PP3 -44.6340 -22.7228
#> PP4 -44.6334 -22.7228
#> BP4 -44.6212 -22.7262
#> BP2 -44.6155 -22.7289
#> PT1 -44.6170 -22.7350
## Matriz de distância geográfica
Dist.km <- as.dist(rdist.earth(bocaina.xy, miles=F)) # matriz de distância geográfica (geodésica) considerando a curvatura da Terra
## Padronizações
comp.bo.pad <- decostand(t(bocaina), "hellinger")
env.bocaina <- decostand(bocaina.env[,-9], "standardize")
## Dissimilaridades
dissimil.bocaina <- vegdist(comp.bo.pad, "bray")
dissimil.env <- vegdist(env.bocaina, "euclidian")Vamos verificar a correlação entre a distância geográfica em linha reta e a dissimilaridade ambiental (Figura 9.19)
## Mantel
# Espaço vs. ambiente
mantel(Dist.km, dissimil.env)
#>
#> Mantel statistic based on Pearson's product-moment correlation
#>
#> Call:
#> mantel(xdis = Dist.km, ydis = dissimil.env)
#>
#> Mantel statistic r: 0.4848
#> Significance: 0.005
#>
#> Upper quantiles of permutations (null model):
#> 90% 95% 97.5% 99%
#> 0.250 0.330 0.393 0.447
#> Permutation: free
#> Number of permutations: 999
## Preparar os dados para o gráfico
matrix.dist.env <- data.frame(x = melt(as.matrix(Dist.km))$value,
y = melt(as.matrix(dissimil.env))$value)
## Gráfico
ggplot(matrix.dist.env , aes(x, y)) +
geom_point(size = 4, shape = 21, fill = "darkorange", alpha = 0.7) +
labs(x = "Distância geográfica (km)",
y = "Dissimilaridade Ambiental") +
tema_livro() 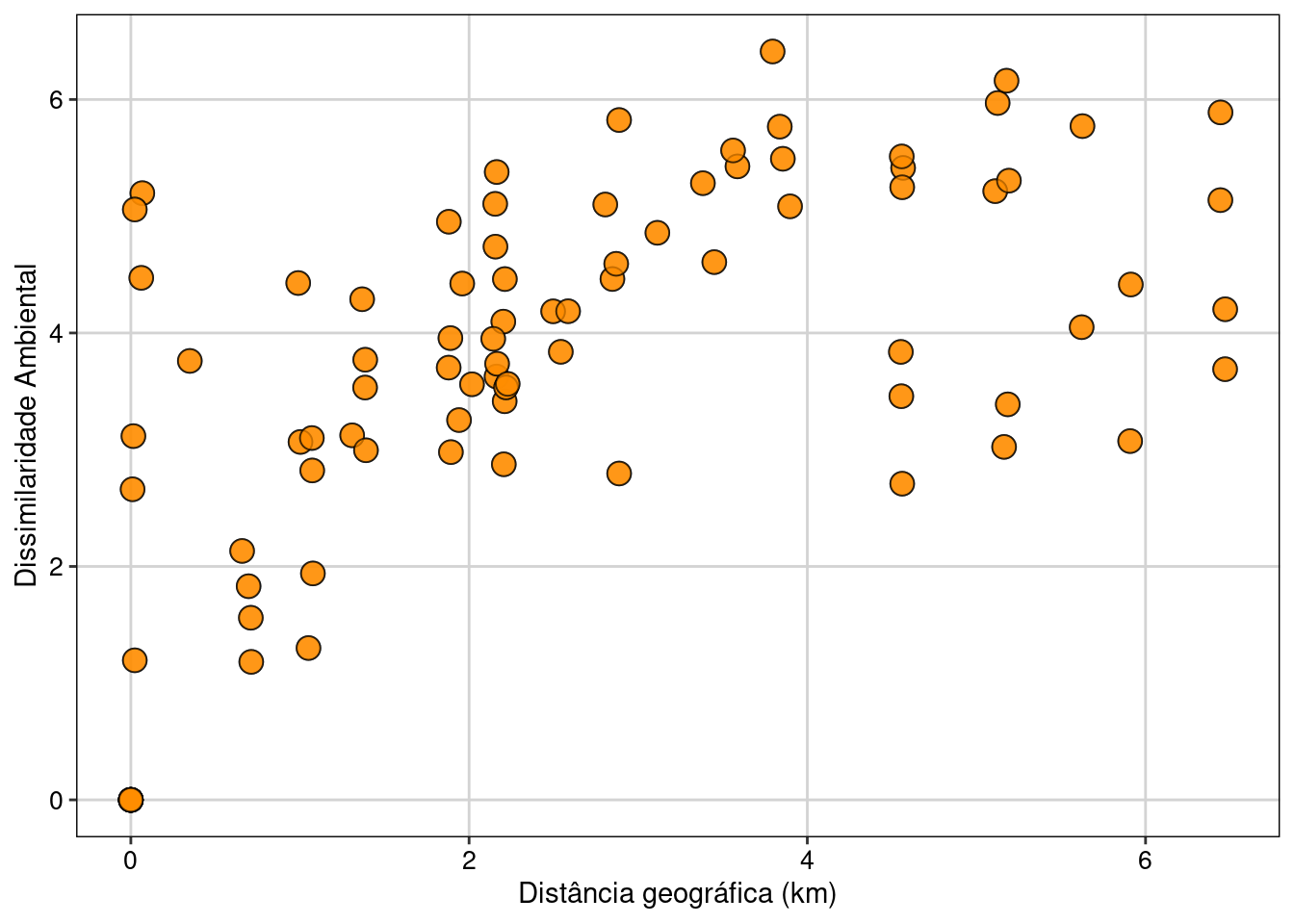
Figura 9.19: Relação das matrizes de (dis)similaridade dos dados.
Vamos verificar a correlação entre a distância geográfica em linha reta e a dissimilaridade na composição de espécies (Figura 9.20)
## Mantel
# Espaço vs. composição
mantel(Dist.km, dissimil.bocaina)
#>
#> Mantel statistic based on Pearson's product-moment correlation
#>
#> Call:
#> mantel(xdis = Dist.km, ydis = dissimil.bocaina)
#>
#> Mantel statistic r: 0.3745
#> Significance: 0.007
#>
#> Upper quantiles of permutations (null model):
#> 90% 95% 97.5% 99%
#> 0.149 0.215 0.279 0.335
#> Permutation: free
#> Number of permutations: 999
## Preparar os dados para o gráfico
matrix.dist.bocaina <- data.frame(x = melt(as.matrix(Dist.km))$value,
y = melt(as.matrix(dissimil.bocaina))$value)
## Gráfico
ggplot(matrix.dist.bocaina , aes(x, y)) +
geom_point(size = 4, shape = 21, fill = "darkorange", alpha = 0.7) +
labs(x = "Distância geográfica (km)",
y = "Dissimilaridade (Bray-Curtis)") +
tema_livro()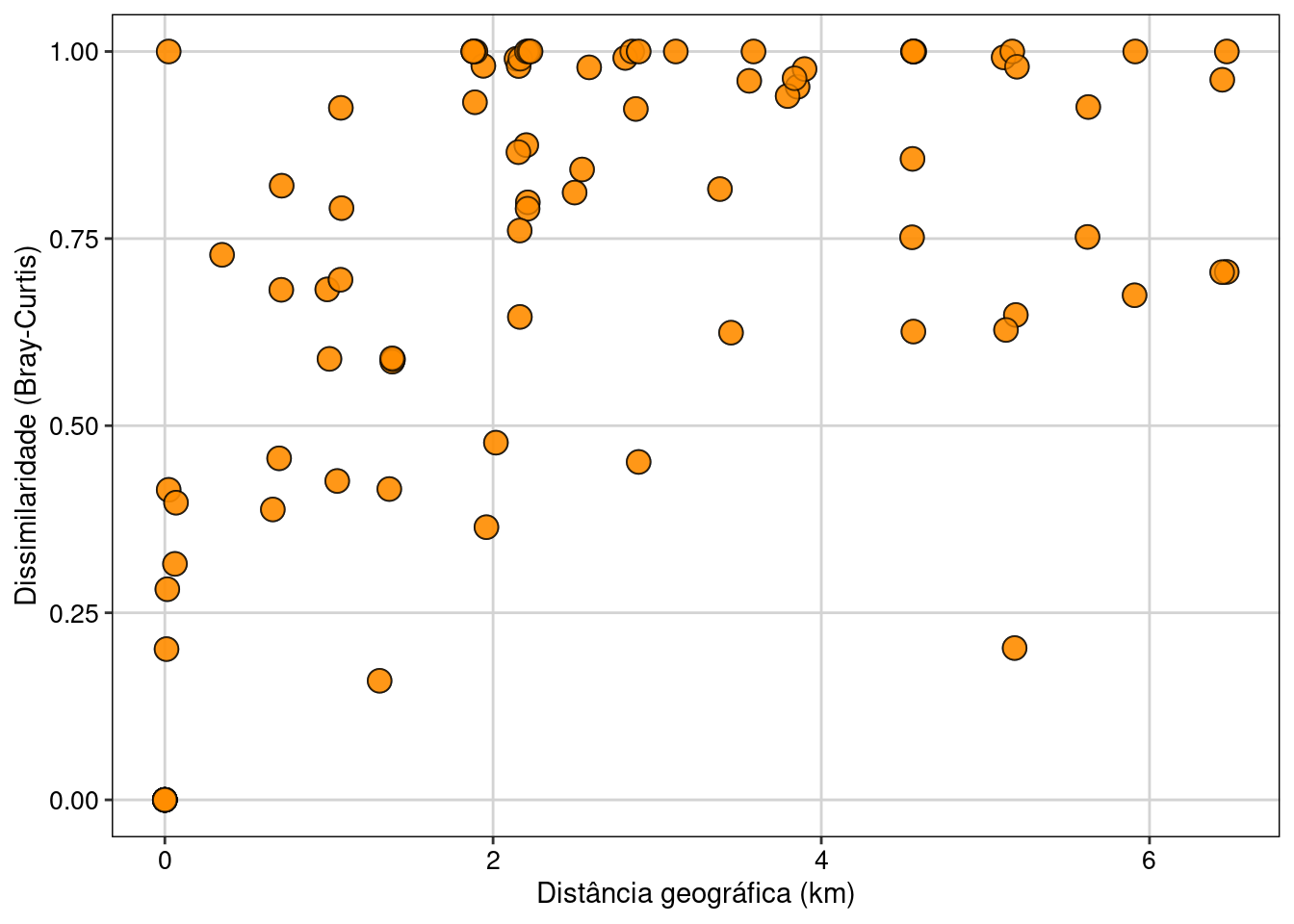
Figura 9.20: Relação das matrizes de (dis)similaridade dos dados.
Vamos verificar a correlação entre a dissimilaridade ambiental e a dissimilaridade na composição de espécies (Figura 9.21)
## Mantel
# Ambiente vs. composição
mantel(dissimil.env, dissimil.bocaina)
#>
#> Mantel statistic based on Pearson's product-moment correlation
#>
#> Call:
#> mantel(xdis = dissimil.env, ydis = dissimil.bocaina)
#>
#> Mantel statistic r: 0.2898
#> Significance: 0.02
#>
#> Upper quantiles of permutations (null model):
#> 90% 95% 97.5% 99%
#> 0.171 0.227 0.266 0.322
#> Permutation: free
#> Number of permutations: 999
## Preparar os dados para o gráfico
matrix.bocaina.env <- data.frame(x = melt(as.matrix(dissimil.bocaina))$value,
y = melt(as.matrix(dissimil.env))$value)
## Gráfico
ggplot(matrix.bocaina.env, aes(x, y)) +
geom_point(size = 4, shape = 21, fill = "darkorange", alpha = 0.7) +
labs(x = "Similaridade Bocaina",
y = "Similaridade Ambiental") +
tema_livro()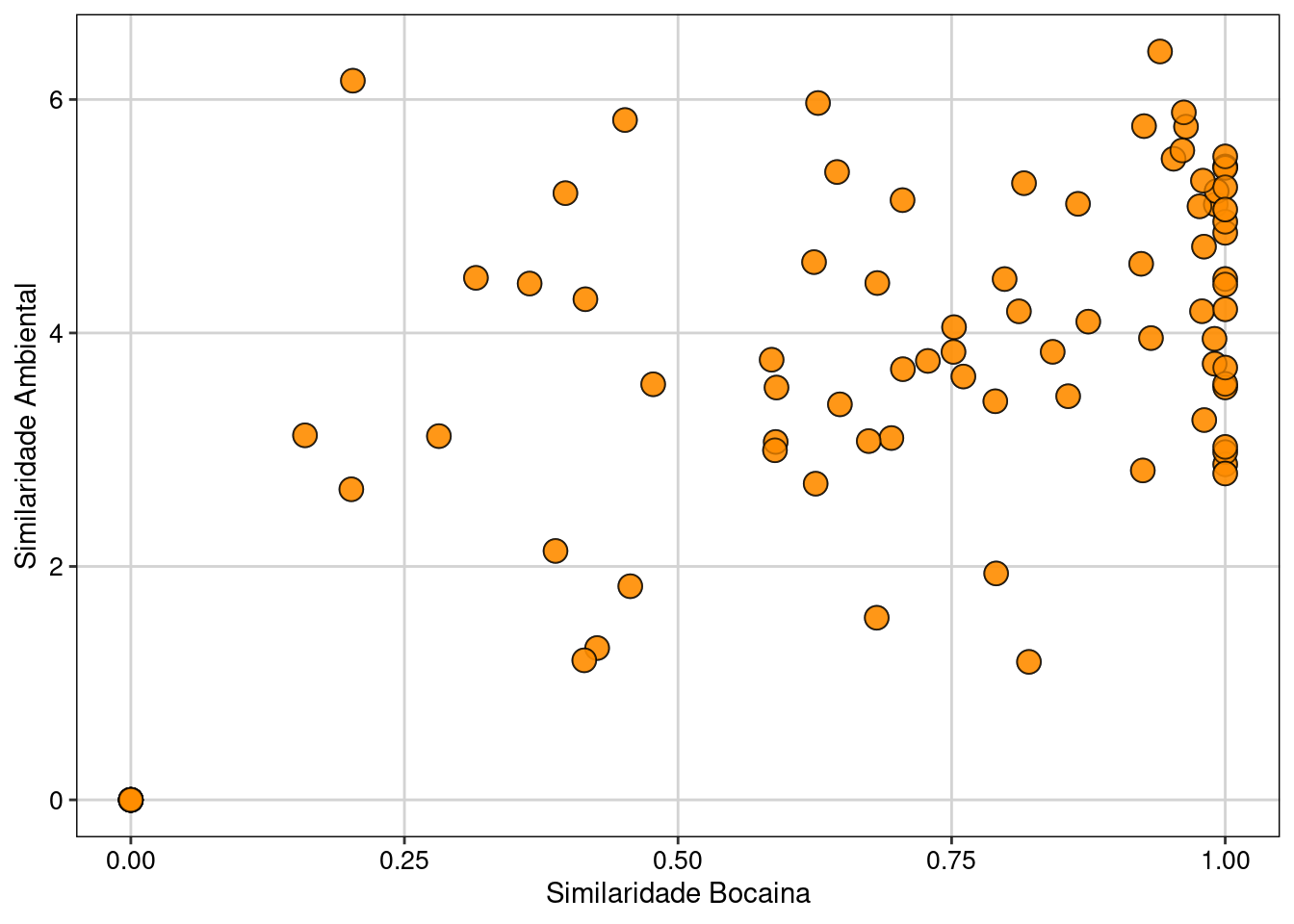
Figura 9.21: Relação das matrizes de (dis)similaridade dos dados.
Interpretação dos resultados
Os resultados mostraram que existe uma relação positiva, embora fraca, entre a dissimilaridade ambiental e a dissimilaridade na composição de espécies. Este resultado está de acordo com a nossa hipótese inicial. No entanto, vimos também que existe uma relação positiva e significativa entre a distância em linha reta entre as poças e a dissimilaridade ambiental. Logo, para de fato testar a relação entre o ambiente e a composição de espécies temos de levar em conta o espaço.
Para isto temos de realizar um teste de Mantel Parcial.
## Mantel Parcial
mantel.partial(dissimil.bocaina, dissimil.env, Dist.km) #comp. vs. ambiente controlando o espaço
#>
#> Partial Mantel statistic based on Pearson's product-moment correlation
#>
#> Call:
#> mantel.partial(xdis = dissimil.bocaina, ydis = dissimil.env, zdis = Dist.km)
#>
#> Mantel statistic r: 0.1334
#> Significance: 0.123
#>
#> Upper quantiles of permutations (null model):
#> 90% 95% 97.5% 99%
#> 0.148 0.200 0.229 0.278
#> Permutation: free
#> Number of permutations: 999Agora sim, vimos que a relação entre ambiente e espécies se mantém, mas que a força dessa relação diminuiu bastante (veja o valor de r) quando controlamos o espaço.
9.8 Mantel espacial com modelo nulo restrito considerando autocorrelação espacial
Embora seja um tipo de análise bastante popular, o Mantel e a sua versão parcial parecem não ser muito adequadas para lidar com autocorrelação espacial. Os autores dos artigos abaixo sugerem inclusive que esse tipo de análise não é adequado para testar a maioria das hipóteses em Ecologia, incluindo diversidade beta. Esse é um tema bastante discutido na literatura e não vamos nos alongar muito sobre isso, mas referimos o(a) leitor(a) para os seguintes artigos chave: Legendre et al. (2015), Legendre & Fortin (2010), e Legendre (2000).
No entanto, Crabot et al. (2019) propuseram uma modificação no teste que leva em conta autocorrelação espacial ao gerar o modelo nulo usado para o teste de hipótese. É utilizado um procedimento chamado Moran Spectral Randomization porque preserva a autocorrelação global medida por meio do I de Moran global. A grande vantagem é que este teste utiliza toda a flexibilidade dos Moran Eigenvector Maps (MEMs), que é apresentado na parte de RDA, permitindo analisar relações entre as matrizes em múltiplas escalas espaciais. Vejamos como o teste funciona.
Primeiro precisamos construir um objeto com as duas matrizes que desejamos testar, no nosso caso composição de espécies e espaço. Depois precisamos construir explicitamente a nossa hipótese de relação espacial entre os locais por meio de uma rede de vizinhança. Esta rede é uma estrutura que nos dirá como (e eventualmente com qual intensidade) se há relação entre os locais. Aqui, entende-se que nos referimos à probabilidade de fluxo de indivíduos entre os locais.
## Mantel
compos_espac <- mantel.randtest(sqrt(dissimil.bocaina), Dist.km)
compos_espac
#> Monte-Carlo test
#> Call: mantel.randtest(m1 = sqrt(dissimil.bocaina), m2 = Dist.km)
#>
#> Observation: 0.3738076
#>
#> Based on 999 replicates
#> Simulated p-value: 0.005
#> Alternative hypothesis: greater
#>
#> Std.Obs Expectation Variance
#> 3.265589171 0.002421976 0.012933827Note que até aqui não há nada de novo, apenas utilizamos uma função diferente para realizar o teste de Mantel, agora no pacote ade4 ao invés do vegan. Agora temos de construir a nossa rede de vizinhança. Optamos neste exemplo por uma rede bastante simples, que é a Minimum Spanning Tree. Essa é a rede espacial mínima que mantém todos os pontos ligados entre si (Figura 9.22).
## Minimum Spanning Tree
nb.boc <- mst.nb(Dist.km) # calcula uma Minimum Spanning Tree
plot(nb.boc, bocaina.xy)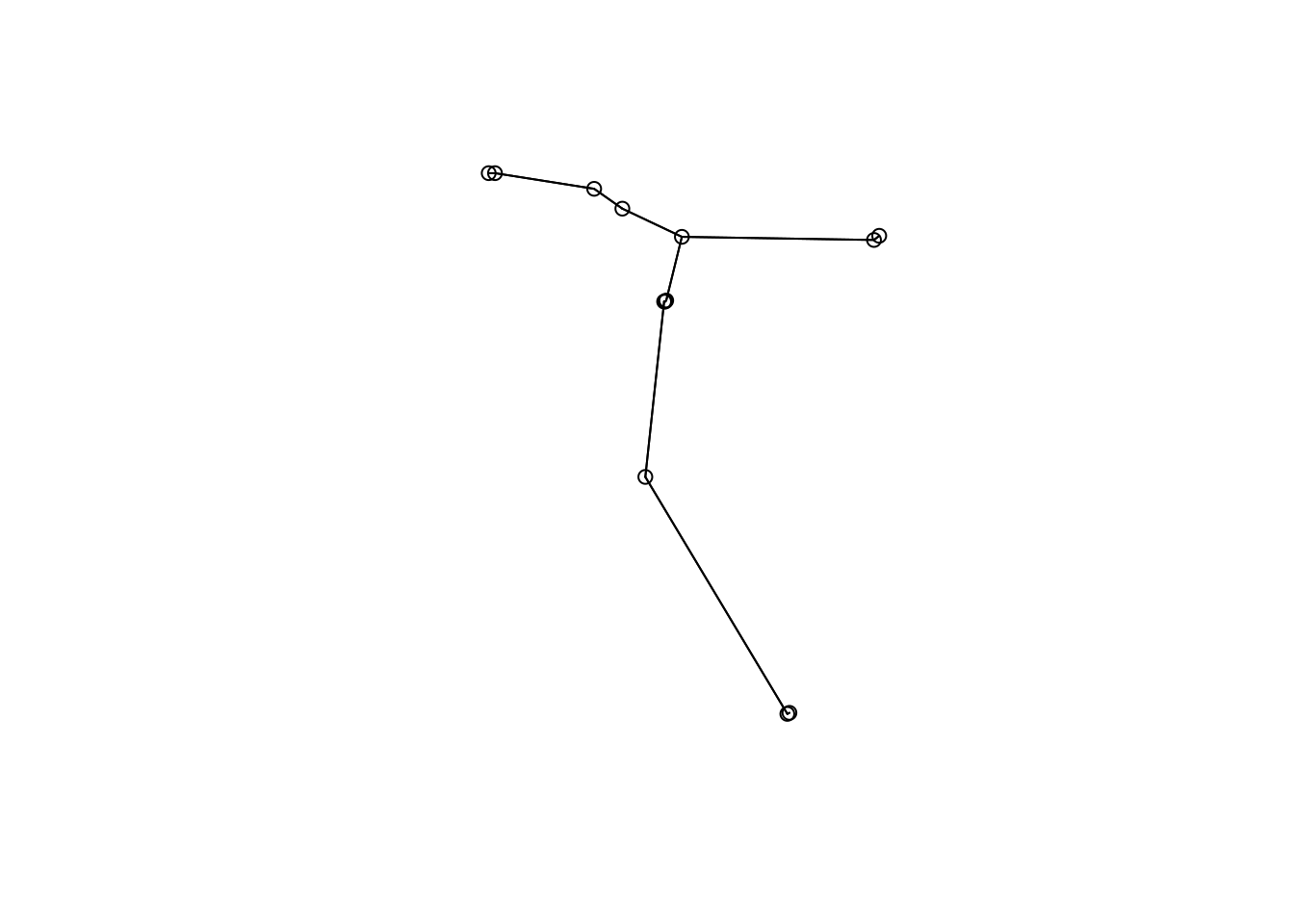
Figura 9.22: Rede de vizinhança com a Minimum Spanning Tree
No gráfico, podemos ver a “cara” da rede. Cada ponto representa um local (poça) e as linhas representam a ligação hipotética entre eles, plotamos no espaço geográfico, ou seja, o Norte aponta pra cima. Agora temos apenas que converter o formato nb para listw e finalmente entrar com esses objetos na função que realizará a análise.
## Conversão
lw <- nb2listw(nb.boc)
## Mantel espacial
msr(compos_espac, lw, method = "pair")
#> Monte-Carlo test
#> Call: msr.mantelrtest(x = compos_espac, listwORorthobasis = lw, method = "pair")
#>
#> Observation: 0.3738076
#>
#> Based on 999 replicates
#> Simulated p-value: 0.127
#> Alternative hypothesis: greater
#>
#> Std.Obs Expectation Variance
#> 1.21335033 0.17433665 0.02702631Interpretação dos resultados
Vamos comparar com o Mantel comum.
## Mantel comum
compos_espac
#> Monte-Carlo test
#> Call: mantel.randtest(m1 = sqrt(dissimil.bocaina), m2 = Dist.km)
#>
#> Observation: 0.3738076
#>
#> Based on 999 replicates
#> Simulated p-value: 0.005
#> Alternative hypothesis: greater
#>
#> Std.Obs Expectation Variance
#> 3.265589171 0.002421976 0.012933827Note que o valor da estatística do teste, ou seja, o r de Mantel é exatamente o mesmo. No entanto, o valor de P que indicava que o teste havia sido significativo anteriormente mudou e passou a ser não significativo. Isso ocorreu porque, embora a maneira de calcular a estatística do teste seja a mesma, a forma de construir a distribuição nula, a partir da qual será calculado o valor de P mudou drasticamente, resultando num teste não significativo.
9.9 PROCRUSTES e PROTEST
Uma alternativa ao Mantel para comparar o grau de associação entre conjuntos multidimensionais de dados (e.g., matriz de espécies e matriz ambiental) é a análise conhecida como Procrustes (Gower 1971; Jackson 1995). Esta análise compara duas matrizes (objetos nas linhas e variáveis nas colunas) minimizando a soma dos desvios quadrados entre os valores através das seguintes técnicas: translação, escalonamento e rotação. É importante notar que os objetos devem ser os mesmos e, desse modo, o número de linhas é obrigatoriamente igual, ao passo que o número de colunas pode variar. A posição do objeto Xi (i = 1, …n) é comparada com o objeto Yi da matriz correspondente, movimentando os pontos via translação, reflexão, rotação e dilatação. Assim, os objetos da matriz X resultam na matriz X’ que é representada pelo melhor ajuste (menor valor residual da soma dos quadrados: estatística m12) entre a matriz X e Y. A estatística m12 mede, então, o grau de concordância entre as duas matrizes. Os valores de m12 variam de 1 (sem concordância) a 0 (máxima concordância) (Peres-Neto and Jackson 2001; Lisboa et al. 2014). Para testar a significância do valor observado de m12, Jackson (1995) sugeriu um teste de aleatorização chamado PROTEST.
As possibilidades de aplicação do Procrustes para ecologia são diversas. Dentre elas, se destacam a: i) morfometria geométrica e ii) ecologia de comunidades (concordância de comunidades). Uma característica interessante do Procrustes é a possibilidade de usar matriz bruta (e.g., variáveis ambientais) ou matriz de distância, o que amplia as possibilidades analíticas. Para comparações com matrizes brutas, análises de ordenação irrestrita (PCA, CA) devem ser realizadas antes do Procrustes. Por outro lado, para comparações com matrizes de distância (e.g., Euclidiana, Jaccard, Bray-Curtis), análises como PCoA e nMDS devem preceder à análise de Procrustes (veja Figura 4 em Peres-Neto and Jackson 2001). Nos dois casos, a ordenação é importante para gerar matrizes com a mesma dimensionalidade o que, por sua vez, permite comparar matrizes com número de colunas diferentes.
Exemplo 1
Neste exemplo, vamos utilizar dois conjuntos de dados simulados de peixes e macroinvertebrados aquáticos coletados em riachos. Neste exemplo hipotético, existe uma rede de 12 riachos com diferentes graus de poluição. Em cada riacho, foi produzida uma lista de espécies de peixes e de macroinvertebrados (com dados de abundância).
Pergunta
- Existe concordância na distribuição na composição de espécies de peixes e macroinvertebrados?
Predições
- Assumindo que alguns poluentes, tais como metais pesados, podem atuar como filtro ambiental e limitar a ocorrência de determinados organismos aquáticos, espera-se encontrar alta concordância entre as duas matrizes (peixes e macroinvertebrados). Ou seja, a comunidade tanto de peixes quanto de macroinvertebrados responderão de forma similar ao gradiente ambiental
Variáveis
- Variáveis: composição das espécies de peixes e macroinverebrados aquáticos
Análises
No exemplo escolhido, as duas matrizes representam a composição de espécies em diferentes riachos. Desse modo, o ideal é transformar esta matriz bruta em matriz de distância com o método Bray-Curtis (vegdist()). O próximo passo, então, é realizar uma Análise de Coordenadas Principais (PCoA) (veja abaixo) para gerar duas matrizes de ordenação que serão comparadas com a função procrustes(). Por fim, utilizamos a função protest() para testar a significância da concordância entre as matrizes (Figura 9.23).
## Dados
head(fish_comm)
#> sp1 sp2 sp3 sp4 sp5 sp6 sp7 sp8 sp9 sp10 sp11 sp12 sp13 sp14 sp15 sp16 sp17 sp18 sp19 sp20 sp21 sp22 sp23 sp24
#> site1 0 0 0 1 1 0 4 0 0 0 1 0 1 1 0 5 0 0 0 0 0 1 0 3
#> site2 0 0 0 1 0 1 5 0 2 1 1 2 1 0 0 1 0 0 0 0 0 0 1 0
#> site3 0 1 0 4 0 0 0 1 5 0 5 0 0 5 0 1 0 1 0 0 2 0 0 0
#> site4 0 5 0 1 0 1 0 0 2 0 0 0 0 2 1 0 0 0 0 1 1 0 0 2
#> site5 0 2 0 0 0 0 0 0 0 0 4 0 0 1 0 4 0 0 0 1 5 0 5 0
#> site6 0 2 1 0 0 0 0 1 1 0 0 2 0 2 0 0 0 0 0 0 0 0 4 0
head(macroinv)
#> sp1 sp2 sp3 sp4 sp5 sp6 sp7 sp8 sp9 sp10 sp11 sp12 sp13 sp14 sp15 sp16 sp17 sp18 sp19 sp20 sp21 sp22 sp23 sp24 sp25 sp26 sp27 sp28 sp29
#> site1 0 1 1 0 0 0 0 0 0 1 2 0 0 0 0 1 1 0 4 0 0 0 1 0 0 1 0 4 0
#> site2 0 2 1 0 0 0 0 1 1 0 0 2 0 1 1 0 0 0 0 0 0 1 2 0 1 0 1 1 0
#> site3 0 0 0 1 0 1 5 0 2 1 1 2 0 4 0 1 0 0 1 0 0 0 0 1 0 2 1 0 0
#> site4 0 1 0 4 0 0 0 1 5 0 5 0 0 5 0 1 0 1 0 0 2 0 0 0 0 2 1 0 0
#> site5 0 2 0 0 0 0 0 0 0 0 4 0 0 2 1 0 0 0 0 1 1 0 0 2 0 5 0 1 0
#> site6 1 0 0 1 0 0 0 0 0 0 1 0 0 2 0 0 0 0 0 0 0 0 4 0 0 2 0 0 0
#> sp30 sp31 sp32 sp33 sp34 sp35 sp36
#> site1 0 0 1 5 0 5 0
#> site2 0 1 0 0 1 0 0
#> site3 0 0 1 1 0 0 2
#> site4 0 0 0 0 5 1 0
#> site5 1 0 0 2 0 0 0
#> site6 0 0 0 0 0 4 0
## Fixar a amostragem
set.seed(1001)
## Matrizes de distância de PCoA
d_macro <- vegdist(macroinv, "bray")
pcoa_macro <- cmdscale(d_macro)
d_fish <- vegdist(fish_comm, "bray")
pcoa_fish <- cmdscale(d_fish)
## PROCRUSTES
concord <- procrustes(pcoa_macro, pcoa_fish)
protest(pcoa_macro, pcoa_fish)
#>
#> Call:
#> protest(X = pcoa_macro, Y = pcoa_fish)
#>
#> Procrustes Sum of Squares (m12 squared): 0.6185
#> Correlation in a symmetric Procrustes rotation: 0.6176
#> Significance: 0.019
#>
#> Permutation: free
#> Number of permutations: 999
## Gráfico
plot(concord, main = "",
xlab = "Dimensão 1",
ylab = "Dimensão 2")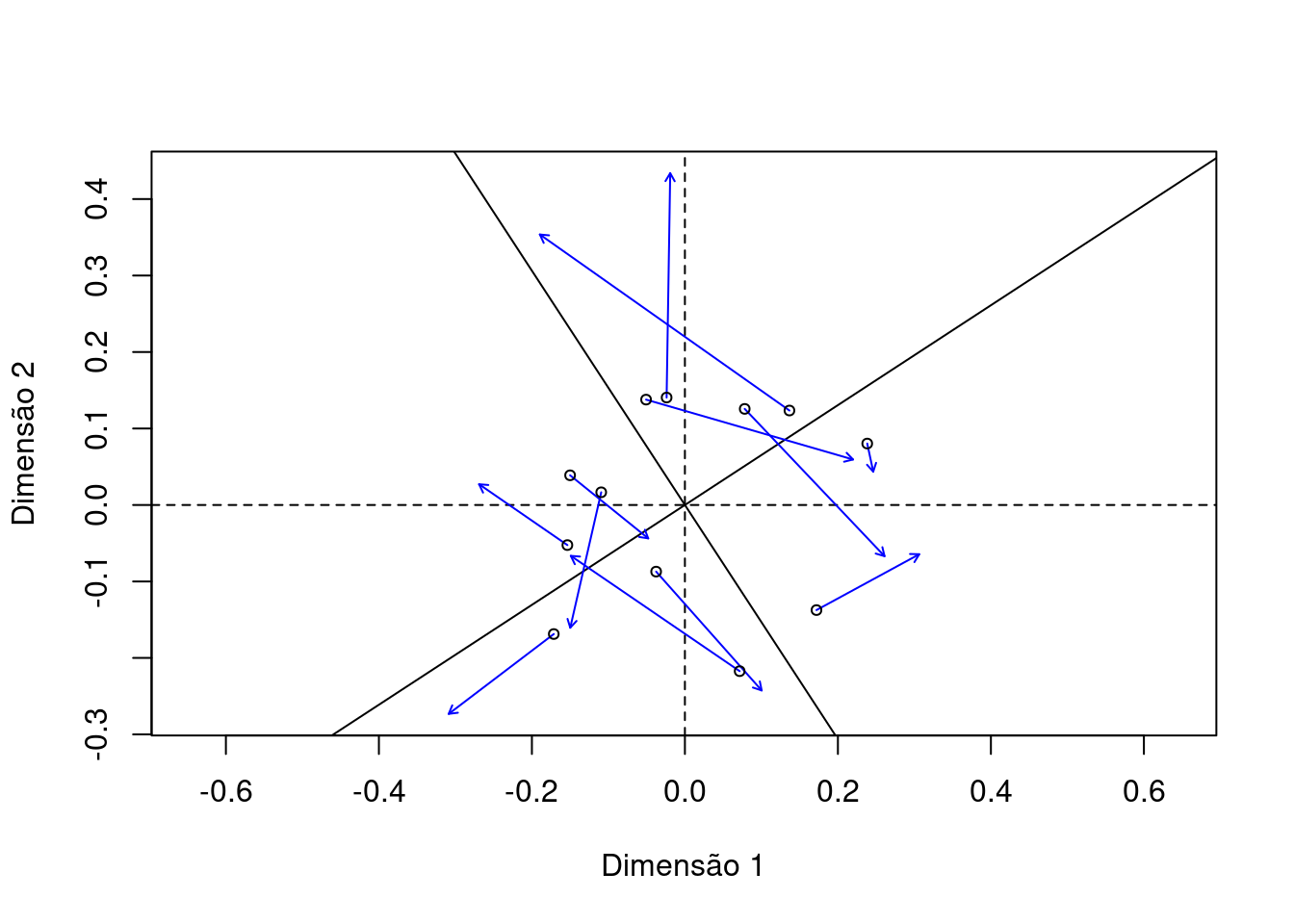
Figura 9.23: Biplot mostrando o resultado da análise de PROCRUSTES.
Interpretação dos resultados
A função protest() apresenta dois resultados importantes: i) a estatística m12 e ii) o valor de significância (p). No exemplo, o valor de m12 é igual a 0.6185 e o valor de p é 0,019. Desse modo, podemos concluir que existe concordância entre a composição de espécies de peixes e macroinvertebrados aquáticos, sugerindo que o nível de poluição pode gerar padrões previsíveis de distribuição de diferentes organismos aquáticos. A figura produzida pelo código plot(concord) mostra um gráfico típico do Procrustes, onde a base da seta representa a matriz X e a ponta da seta a matriz alvo (Y) após a rotação para comparar o grau de concordância entre X e Y. Cada ponto representa um objeto (linha) das matrizes X e Y. Quanto menor for o tamanho das setas, mais concordantes são as observações em cada objeto.
9.10 Métodos multivariados baseados em modelos
Mais recentemente, alguns autores têm proposto métodos multivariados baseados em modelos. Estes métodos têm se diversificado hoje em dia e existem pacotes que realizam praticamente todas as análises que vimos acima, com a diferença que utilizam distribuições de probabilidade dado um modelo (e.g., Poisson) ao invés de coeficientes de dissimilaridades. Vamos exemplificar o uso de um desses métodos, mas não vamos fazer uma revisão extensiva. Caso o(a) leitor(a) deseje conhecer mais, recomendamos consultar principalmente os pacotes gllvm, ecoCopula e Hmsc.
Um dos primeiros métodos foi proposto em 2012 pelo grupo de David Warton (Warton, Wright, and Wang 2012), implementado no pacote mvabund. Anteriormente neste mesmo ano foi publicado um artigo pelo mesmo grupo (Wang et al. 2012) em que os autores demonstraram que métodos baseados em dissimilaridade, especialmente PERMANOVA, não conseguem modelar adequadamente dados multivariados de contagem (e.g., abundância) por não levarem em conta a relação monotônica entre média e variância. Vejamos o que isso quer dizer utilizando os dados do artigo de da Silva et al. (2017) (Figura 9.24).
## Dados com seis primeiras localidades e espécies
head(anuros_permanova)[1:6]
#> Chiasmocleis_albopunctata Dendropsophus_elianae Dendropsophus_jimi Dendropsophus_nanus Dendropsophus_minutus
#> Araras 6 0 0 0 1
#> Artur Nogueira 0 0 0 0 6
#> Conchal 0 0 0 0 0
#> Engenheiro Coelho 1 0 0 0 2
#> Jaguari\xfana 8 0 0 0 0
#> Limeira 0 11 15 0 15
#> Dendropsophus_sanborni
#> Araras 0
#> Artur Nogueira 0
#> Conchal 0
#> Engenheiro Coelho 0
#> Jaguari\xfana 0
#> Limeira 0
#retirando a coluna que contém o fator e deixando apenas dados de abundância
anuros_abund <- as.data.frame(anuros_permanova[,-28])
#incluindo apenas o fator a ser testado no modelo
grupos <- factor(anuros_permanova[,28])
## Média-variância
# criando um objeto da classe mvabund com os dados de abundância
abund_tr <- mvabund(anuros_abund)
meanvar.plot(abund_tr)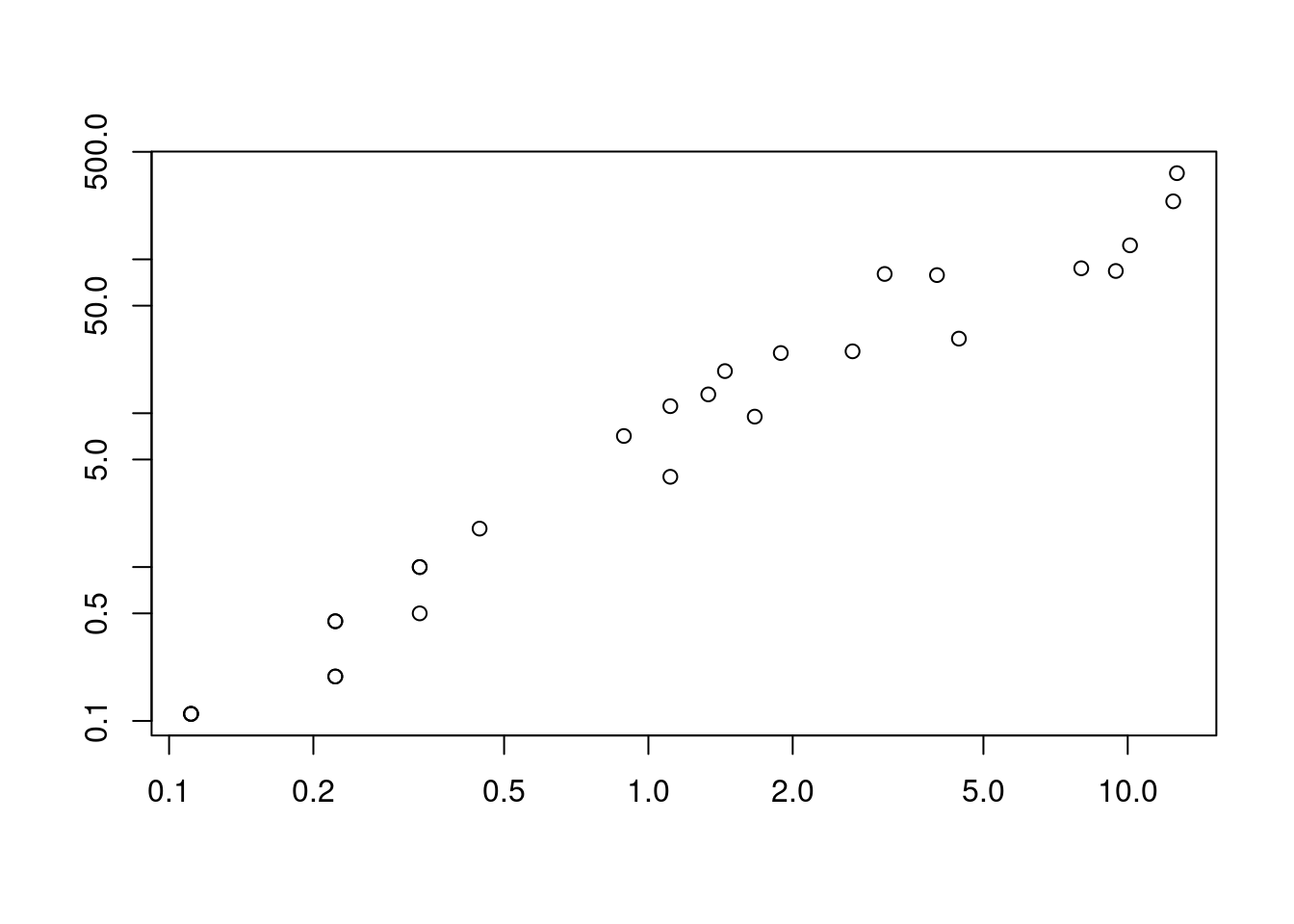
Figura 9.24: Gráfico mostrando a média-variância para dados de abundância multivariada.
Este conjunto de dados contém abundâncias de anfíbios coletados num conjunto de cidades do interior de São Paulo e também sua presença em museus. Aqui, vemos que há uma clara relação monotônica entre a média e a variância da abundância das espécies na matriz. Ou seja, à medida que espécies aumentam sua média de abundância, elas também aumentam quase que proporcionalmente a sua variância. Esta é uma propriedade bastante comum de dados multivariados de contagem, mas que não é muito bem modelada por métodos baseados em dissimilaridade, já que nesse caso apenas as espécies mais abundantes têm de fato um peso na análise.
A proposta implementada no pacote mvabund é baseada em Modelos Lineares Generalizados (GLMs) que você já conhece do Capítulo 8. Ou seja, este método permite que sejam modeladas as abundâncias das espécies num contexto multivariado utilizando explicitamente distribuições de probabilidade, tais como aquelas que utilizamos (e.g., Poisson, Binomial negativa, etc.). Isso faz com que demos peso semelhante às espécies. Vejamos um exemplo de como o modelo é ajustado e como é feito teste de hipótese.
Exemplo 1
A principal pergunta do artigo citado acima foi testar se a composição de espécies que obtemos em campo e de coleção científicas é diferente. Isso tem implicações para levantamentos de fauna, já que podemos complementar um tipo de dado com outro ou saber se eles são redundantes. Aqui, grupos é apenas um fator que indica se aquela linha da matriz apresenta dados obtidos em campo ou coleção. Vamos testar a hipótese nula de que não há diferença na composição entre as duas fontes de dados ajustando um modelo com distribuição binomial negativa (Figura 9.25).
## Gráfico
plot(abund_tr ~ grupos, cex.axis = 0.8, cex = 0.8)
#>
#> PIPING TO 2nd MVFACTOR
## Modelo
modelo1 <- manyglm(abund_tr ~ grupos, family = "negative.binomial")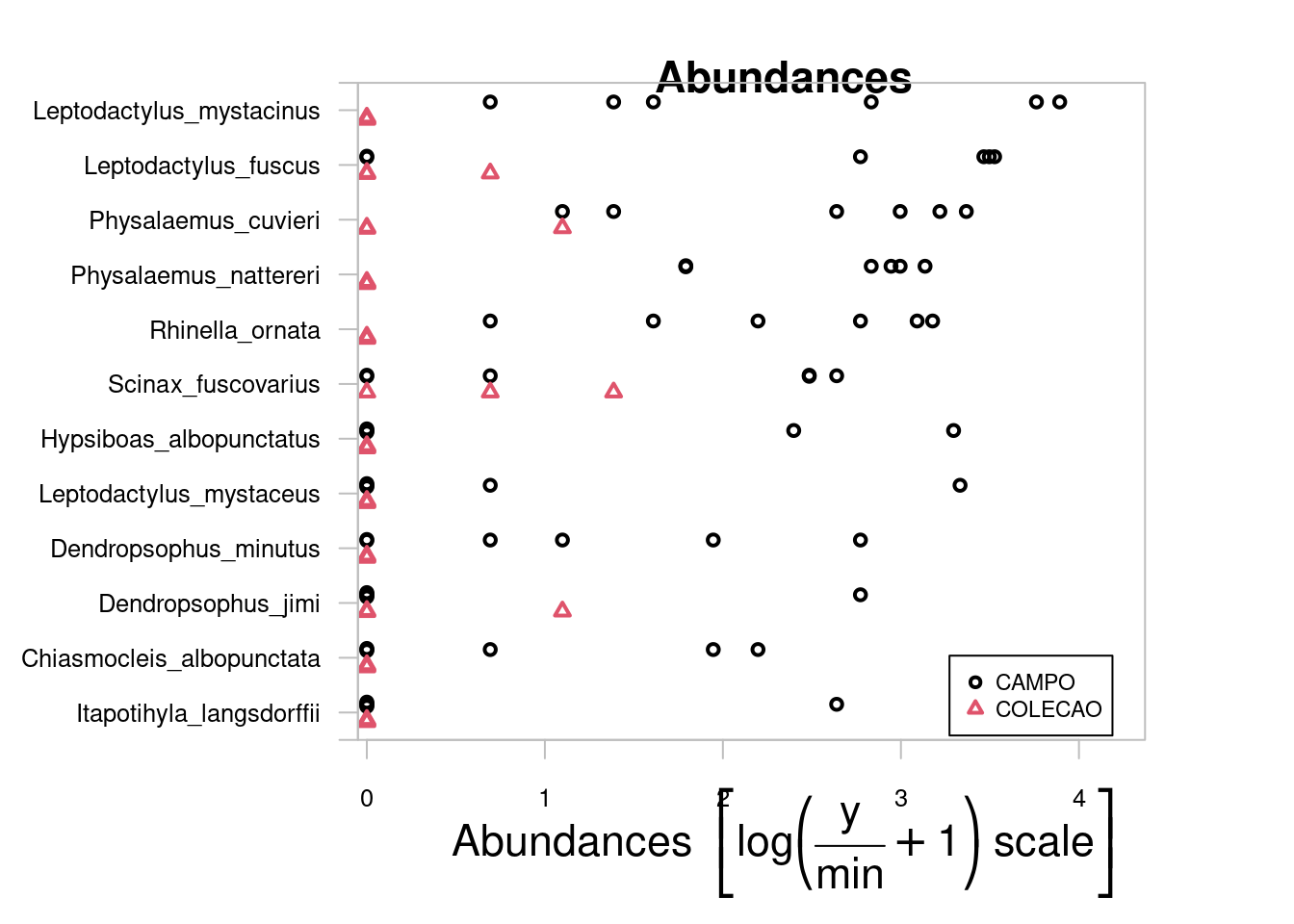
Figura 9.25: Gráfico mostrando as abundâncias para os dois grupos.
O gráfico mostrando os dados possui log da abundância das espécies e o fator (campo vs. coleção). Com essa análise exploratória de dados já podemos identificar se há diferença ou não na abundância das espécies em cada local. Vemos que algumas espécies são bem mais abundantes no campo do que em coleções, tais como Leptodactylus mystacinus e Rhinella ornata.
Uma grande vantagem desse tipo de método baseado em modelos é que, assim como um GLM típico, também podemos realizar diagnose dos resíduos utilizando plots de resíduos versus predito. Vejamos como isso funciona (Figura 9.26).
## Diagnose
plot(modelo1)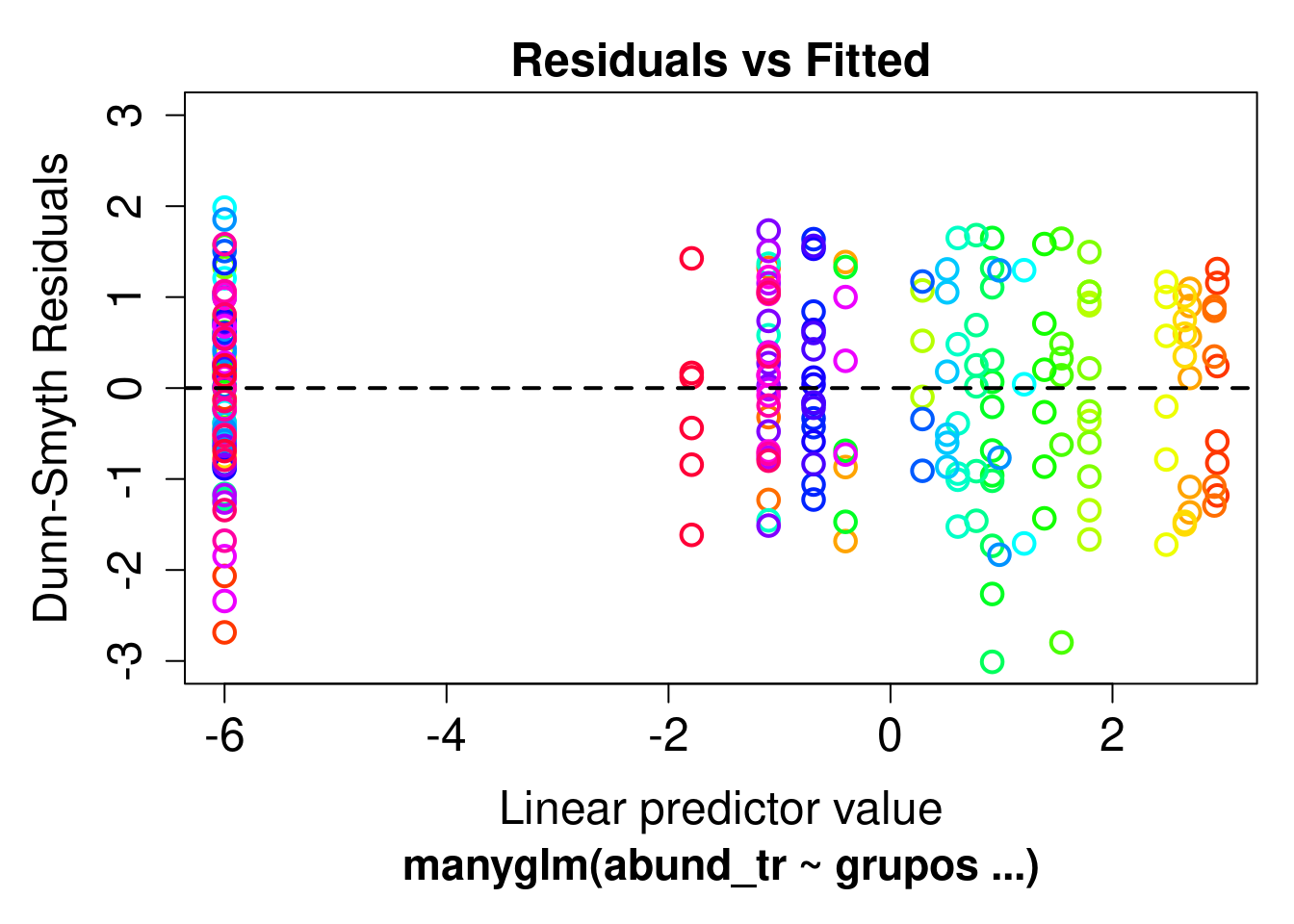
Figura 9.26: Diagnose dos resíduos do modelo ajustado.
Aqui vemos que os dados se distribuem de maneira mais ou menos homogênea e sem um padrão claro ao redor do zero. Isso indica que a distribuição Binomial negativa foi adequada para modelar estes dados. E agora sim podemos interpretar os resultados com mais segurança.
Interpretação dos resultados
## Resultados
summary(modelo1)
#>
#> Test statistics:
#> wald value Pr(>wald)
#> (Intercept) 18.947 0.001 ***
#> gruposCOLECAO 4.727 0.004 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Test statistic: 4.727, p-value: 0.004
#> Arguments:
#> Test statistics calculated assuming response assumed to be uncorrelated
#> P-value calculated using 999 resampling iterations via pit.trap resampling (to account for correlation in testing).Aqui vemos que há sim uma diferença significativa na abundância relativa das espécies entre o campo e coleção. Mas até então estamos levando em conta toda a matriz numa abordagem multivariada. No entanto, não sabemos qual(is) espécie(s) são responsáveis por este padrão. Para investigar isso, podemos realizar uma Análise de Deviance separada para cada espécie, isso é o que a linha abaixo faz.
## ANOVA
anova(modelo1, p.uni = "adjusted")
#> Time elapsed: 0 hr 0 min 6 sec
#> Analysis of Deviance Table
#>
#> Model: abund_tr ~ grupos
#>
#> Multivariate test:
#> Res.Df Df.diff Dev Pr(>Dev)
#> (Intercept) 8
#> grupos 7 1 94.08 0.01 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Univariate Tests:
#> Chiasmocleis_albopunctata Dendropsophus_elianae Dendropsophus_jimi Dendropsophus_nanus
#> Dev Pr(>Dev) Dev Pr(>Dev) Dev Pr(>Dev) Dev Pr(>Dev)
#> (Intercept)
#> grupos 3.308 0.467 0.394 0.836 0.23 0.836 2.197 0.707
#> Dendropsophus_minutus Dendropsophus_sanborni Elachistocleis_cesari Hypsiboas_albopunctatus
#> Dev Pr(>Dev) Dev Pr(>Dev) Dev Pr(>Dev) Dev Pr(>Dev)
#> (Intercept)
#> grupos 4.752 0.309 2.197 0.707 2.012 0.762 2.069 0.762
#> Hypsiboas_faber Hypsiboas_lundii Hypsiboas_prasinus Itapotihyla_langsdorffii Leptodactylus_fuscus
#> Dev Pr(>Dev) Dev Pr(>Dev) Dev Pr(>Dev) Dev Pr(>Dev) Dev
#> (Intercept)
#> grupos 0.913 0.822 0.915 0.822 0.913 0.822 0.911 0.836 4.652
#> Leptodactylus_latrans Leptodactylus_mystaceus Leptodactylus_mystacinus Physalaemus_centralis
#> Pr(>Dev) Dev Pr(>Dev) Dev Pr(>Dev) Dev Pr(>Dev) Dev
#> (Intercept)
#> grupos 0.309 0.811 0.836 1.869 0.783 9.772 0.045 2.639
#> Physalaemus_cuvieri Physalaemus_marmoratus Physalaemus_nattereri Pseudis_paradoxa
#> Pr(>Dev) Dev Pr(>Dev) Dev Pr(>Dev) Dev Pr(>Dev) Dev Pr(>Dev)
#> (Intercept)
#> grupos 0.670 8.221 0.062 1.622 0.783 17.131 0.014 2.67 0.540
#> Rhinella_ornata Rhinella_schneideri Scinax_fuscomarginatus Scinax_fuscovarius Scinax_similis
#> Dev Pr(>Dev) Dev Pr(>Dev) Dev Pr(>Dev) Dev Pr(>Dev) Dev
#> (Intercept)
#> grupos 11.961 0.027 3.363 0.467 2.64 0.622 1.655 0.783 2.646
#> Trachycephalus_typhonius
#> Pr(>Dev) Dev Pr(>Dev)
#> (Intercept)
#> grupos 0.622 1.622 0.783
#> Arguments:
#> Test statistics calculated assuming uncorrelated response (for faster computation)
#> P-value calculated using 999 iterations via PIT-trap resampling.Aqui vemos que algumas espécies já identificadas no plot exploratório de fato são importantes para determinar o padrão, tais como: Leptodactylus mystacinus, Physalaemus nattereri e Rhinella ornata. Essas foram espécies cuja Deviance foi significativa.
9.11 Para se aprofundar
9.11.1 Livros
Listamos a seguir livros e artigos com material que recomendamos para seguir com sua aprendizagem em análises multivariadas em R: i) Legendre & Legendre (2012) Numerical Ecology, ii) Borcard e colaboradores (2018) Numerical Ecology with R, iii) Thioulouse e colaboradores (2018) Multivariate Analysis of Ecological Data with ade4, iv) Ovaskainen & Abrego (2020) Joint Species Distribution Modelling, v) James & McCulloch (1990) Multivariate Analysis in Ecology and Systematics: Panacea or Pandora’s Box? e vi) Dunstan e colaboradores (2011) Model based grouping of species across environmental gradients.
9.12 Exercícios
9.1 Utilize os dados “mite” do pacote vegan para testar o efeito de variáveis ambientais sobre a composição de espécies de ácaros utilizando as seguintes análises: RDA, RDAp (combinada com MEM), dbRDA e PERMANOVA. Após realizar as cinco análises, responda às seguintes perguntas?
A. Quais são as variáveis ambientais (mite.env) mais importantes para a composição de ácaros em cada uma das análises? B. Os vetores espaciais obtidos com a análise MEM explicam a variação na composição de espécies? Eles são mais ou menos importantes do que as variáveis ambientais? C. Discuta as diferenças de interpretação entre a RDA, RDAp, dbRDA e PERMANOVA.
Dados necessários:
9.2
Efetue uma análise de agrupamento pela função hclust(). Lembre-se de dar nome ao objeto para poder plotar o dendrograma depois. Utilize a ajuda para encontrar como entrar com os argumentos da função.
- utilizando o método UPGMA e o índice de Bray-Curtis.
- Faça agora o dendrograma com outro índice de dissimilaridade e compare os resultados. São diferentes? No que eles influenciariam a interpretação do resultado?
9.3 Na perspectiva de metacomunidades (Leibold et al., 2004), a dispersão dos organismos tem um papel proeminente para entender como as espécies estão distribuídas na natureza. Com o objetivo de testar se a dispersão influencia a composição de espécies de cladóceros e copépodos, e portanto a estrutura da metacomunidade, um pesquisador selecionou dois conjuntos de lagos: em um deles todos os lagos são isolados e no outro os lagos são conectados.
Importe o conjunto de dados lagos do pacote
ecodadose responda a pergunta se o fato de os lagos estarem conectados ou não influencia a composição de espécies desses microcrustáceos. Utilize métodos baseados em modelos que você aprendeu ao longo do capítulo para modelar a abundância multivariada.Faça um plot mostrando a abundância relativa das espécies com maior abundância e veja se elas são diferentes entre os tipos lagos. Combine este resultado com o do item anterior para interpretar o resultado final.
9.4
Carregue o pacote MASS para utilizar os dados crabs. Este conjunto traz medidas morfológicas de dois morfo-tipos da espécie de carangueijo Leptograpsus variegatus coletada em Fremantle, Austrália. Calcule uma PCA e veja se existe uma semelhança morfológica entre os dois morfo-tipos. Lembre-se de dar nome
ao objeto e use a função biplot() para plotar o resultado do teste. Dica: a projeção de um objeto perpendicular à seta do descritor fornece a posição aproximada do objeto ao longo desse descritor. A distância dos objetos no espaço cartesiano reflete a distância euclidiana entre eles.