Capítulo 10 Rarefação
Pré-requisitos do capítulo
Pacotes e dados que serão utilizados neste capítulo.
## Pacotes
library(iNEXT)
library(ecodados)
library(ggplot2)
library(vegan)
library(nlme)
library(dplyr)
library(piecewiseSEM)
## Dados
data("mite")
data("mite.xy")
coord <- mite.xy
colnames(coord) <- c("long", "lat")
data("mite.env")
agua <- mite.env[, 2]
dados_rarefacao <- ecodados::rarefacao_morcegos
rarefacao_repteis <- ecodados::rarefacao_repteis
rarefacao_anuros <- ecodados::rarefacao_anuros
dados_amostras <- ecodados::morcegos_rarefacao_amostras10.1 Aspectos teóricos
Uma das grandes dificuldades na comparação da riqueza de espécies (número de espécies) entre comunidades é decorrente da diferença no esforço amostral (e.g. diferença no número de indivíduos, discrepância na quantidade de unidades amostrais ou área amostrada) que inevitavelmente influenciará no número de espécies observadas (Gotelli and Ellison 2012; Roswell, Dushoff, and Winfree 2021). O método de rarefação nos permite comparar o número de espécies entre comunidades quando o tamanho da amostra (e.g. número de unidades amostrais), o esforço amostral (e.g. tempo de amostragem) ou a número de indivíduos não são iguais. A rarefação calcula o número esperado de espécies em cada comunidade tendo como base comparativa um valor em que todas as amostras atinjam um tamanho padrão. Gotelli & Colwell (2001) descrevem dois tipos de curvas de rarefação: i) baseada em indivíduos (individual-based) - as comparações são feitas considerando a abundância da comunidade padronizada pelo menor número de indivíduos, e ii) baseada na amostra (sampled-based) - as comparações são padronizadas pela comunidade com menor número de amostragens.
O método foi formulado considerando a seguinte pergunta: Se considerarmos n indivíduos ou amostras (n < N) para cada comunidade, quantas espécies registraríamos nas comunidades considerando o mesmo número de indivíduos ou amostras?
Gotelli & Colwell (2001) descrevem este método e discutem em detalhes as restrições sobre seu uso na ecologia.
- As amostras a serem comparadas devem ser consistentes do ponto de vista taxonômico, ou seja, todos os indivíduos devem pertencer ao mesmo grupo taxonômico
- As comparações devem ser realizadas somente entre amostras com as mesmas técnicas de coleta. Por exemplo, não é recomendado comparar amostras onde a riqueza de espécies de anuros de uma amostra foi estimada utilizando armadilhas de interceptação e queda e a outra foi estimada por vocalizações em sítios de reprodução
- Os tipos de hábitat onde as amostras são obtidas devem ser semelhantes
- É um método para estimar a riqueza de espécies em uma amostra menor – não pode ser usado para extrapolar a riqueza para amostras maiores
📝 Importante
Esta última restrição foi superada por Colwell et al. (2012) e Chao & Jost (2012), que desenvolveram uma nova abordagem onde os dados podem ser interpolados (rarefeito) para amostras menores e extrapolados para amostras maiores. Além disso, Chao & Jost (2012) propõem a curva de rarefação coverage-based que padroniza as amostras pela cobertura ou totalidade (completeness) da amostra ao invés do tamanho. As rarefações tradicionais apresentam limitações matemáticas que são superadas por essa nova abordagem (Chao and Jost 2012).
10.2 Curva de rarefação baseada no indivíduo (individual-based)
Exemplo prático 1 - Morcegos
Explicação dos dados
Usaremos os dados de espécies de morcegos amostradas em três fragmentos florestais (Breviglieri 2008): i) Mata Ciliar do Córrego Talhadinho com 12 hectares, ii) Mata Ciliar do Córrego dos Tenentes com 10 hectares, e iii) Fazenda Experimental de Pindorama com 128 hectares.
Pergunta
- A riqueza de espécies de morcegos é maior na Fazenda Experimental do que nos fragmentos florestais menores?
Predições
- O número de espécies será maior em fragmentos florestais maiores
Variáveis
- Matriz ou data frame com as abundâncias das espécies de morcegos (variável resposta) registradas nos três fragmentos florestais (variável preditora)
Checklist
- Verificar se a sua matriz ou data frame estão com as espécies nas linhas e os fragmentos florestais nas colunas
Análise
Vamos olhar os dados usando a função head().
## Cabeçalho dos dados
head(dados_rarefacao)
#> MC_Tenentes MC_Talhadinho FF_Experimental
#> Chrotopterus_auritus 0 1 1
#> Phyllostomus_hastatus 0 1 0
#> Phyllostomus_discolor 0 2 2
#> Artibeus_lituratus 17 26 26
#> Artibeus_obscurus 1 4 6
#> Artibeus_planirostris 34 72 52
## Número de indivíduos por local
colSums(dados_rarefacao)
#> MC_Tenentes MC_Talhadinho FF_Experimental
#> 166 413 223Usaremos as funções do pacote iNEXT (iNterpolation e EXTrapolation) para o cálculo da rarefação (Hsieh, Ma, and Chao 2016). Esta função permite estimar a riqueza de espécies utilizando a família Hill-numbers (Hill 1973; explicação dos conceitos da família Hill-numbers está detalhada no Capítulo 12. O argumento q refere-se a família Hill-numbers onde: 0 = riqueza de espécies, 1 = diversidade de Shannon e 2 = diversidade de Simpson. No exemplo abaixo, utilizamos somente q = 0.
## Rarefação
# Datatype refere-se ao tipo de dados que você vai analisar (e.g. abundância, incidência).
# Endpoint refere-se ao valor máximo que você determina para a extrapolação.
resultados_morcegos <- iNEXT(dados_rarefacao, q = 0,
datatype = "abundance", endpoint = 800)Vamos visualizar os resultados (Figura 10.1).
## Gráfico
# type define o tipo de curva de rarefação
# 1 = curva de rarefação baseada no indivíduo ou amostra
# 2 = curva de representatividade da amostra
# 3 = curva de rarefação baseada na representatividade (coverage-based)
ggiNEXT(resultados_morcegos, type = 1) +
geom_vline(xintercept = 166, lty = 2) +
scale_linetype_discrete(labels = c("Interpolado", "Extrapolado")) +
scale_colour_manual(values = c("darkorange", "darkorchid", "cyan4")) +
scale_fill_manual(values = c("darkorange", "darkorchid", "cyan4")) +
labs(x = "Número de indivíduos", y = " Riqueza de espécies") +
tema_livro()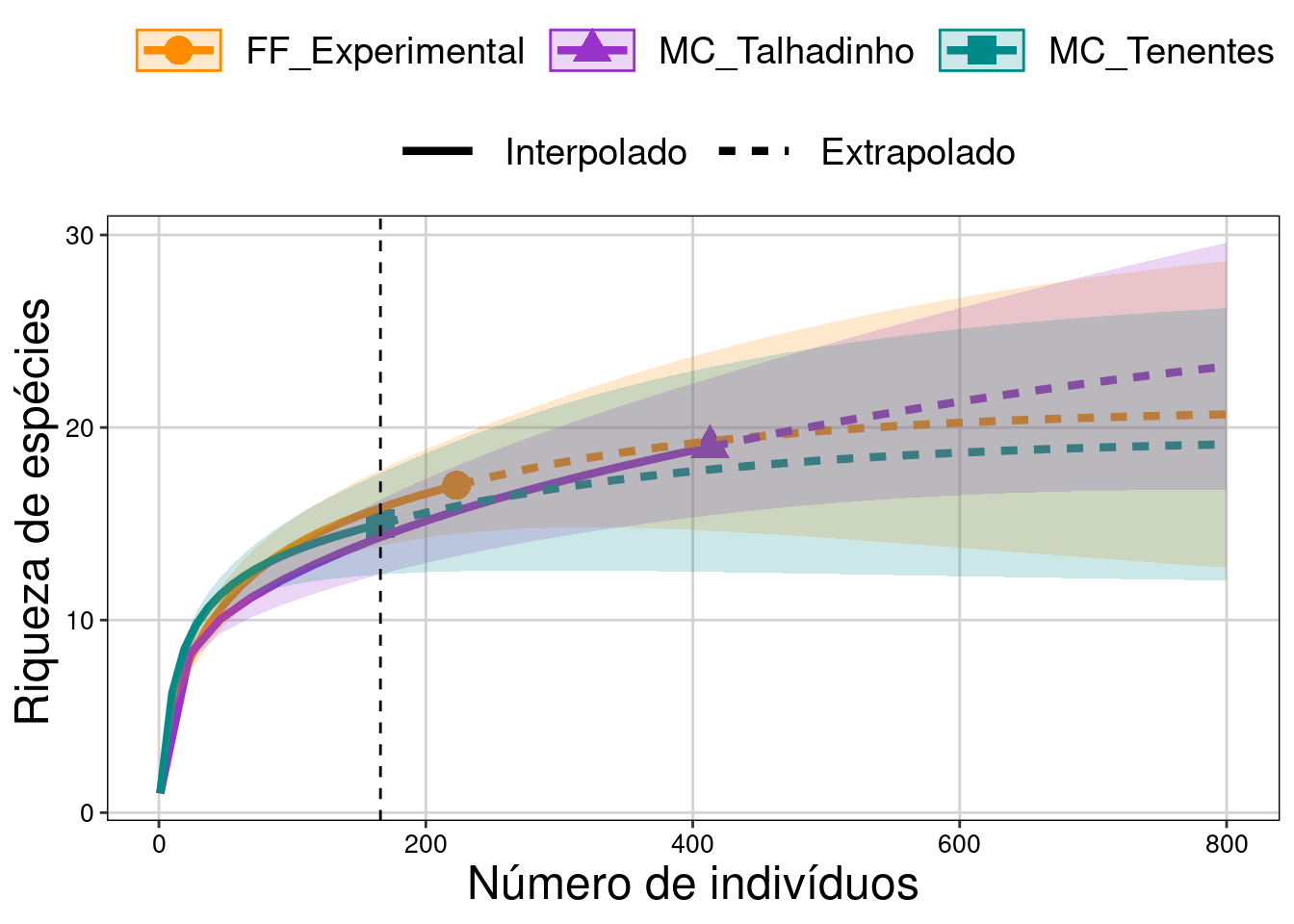
Figura 10.1: Curvas de rarefação baseada nos indivíduos de morcegos.
Interpretação dos resultados
Foram registrados 166 indivíduos na MC_Tenentes, 413 na MC_Talhadinho e 223 na FF_Experimental. Lembrando, você não pode comparar a riqueza de espécies observada diretamente: 15 espécies na MC_Tenentes, 19 espécies na MC_Talhadinho, e 17 espécies no FF_Experimental. A comparação da riqueza de espécies entre as comunidades deve ser feita com base na riqueza de espécies rarefeita, que é calculada com base no número de indivíduos da comunidade com menor abundância (166 indivíduos - linha preta tracejada). Olhando o gráfico é possível perceber que a riqueza de espécies de morcegos rarefeita não é diferente entre os três fragmentos florestais quando corrigimos o problema da diferença na abundância pela rarefação. A interpretação é feita com base no intervalo de confiança de 95%. As curvas serão diferentes quando os intervalos de confiança não se sobreporem (Chao et al. 2014). Percebam que esta abordagem, além da interpolação (rarefação), também realiza extrapolações que podem ser usadas para estimar o número de espécies caso o esforço de coleta fosse maior. Este é o assunto do Capítulo 11.
Exemplo prático 2 - Anuros e Répteis
Explicação dos dados
Neste exemplo, iremos comparar o número de espécies de anuros e répteis (serpentes e lagartos) usando informações dos indivíduos depositados em coleções científicas e coletas de campo (da Silva et al. 2017).
Pergunta
- A riqueza de espécies estimada para uma mesma região é maior usando informações de coleções científicas do que informações de coletas de campo?
Predições
- O número de espécies será maior em coleções científicas devido ao maior esforço amostral (i.e. maior variação temporal para depositar os indivíduos e maior número de pessoas contribuindo com coletas esporádicas)
Variáveis
- Matriz ou data frame com as abundâncias das espécies de anuros e répteis (variável resposta) registradas em coleções científicas e coletas de campo (variável preditora)
Checklist
- Verificar se a sua matriz ou data frame estão com as espécies nas linhas e a fonte dos dados nas colunas
Análise
Olhando os dados dos répteis.
## Cabeçalho
head(rarefacao_repteis)
#> Coleta.Campo Colecoes.Cientificas
#> Ameiva_ameiva 1 0
#> Amphisbaena_mertensii 1 0
#> Apostolepis_dimidiata 0 1
#> Bothrops__itapetiningae 0 2
#> Bothrops__pauloensis 0 1
#> Bothrops_alternatus 0 1Análise usando o pacote iNEXT (Figura 10.2).
## Análise
resultados_repteis <- iNEXT(rarefacao_repteis, q = 0,
datatype = "abundance",
endpoint = 200)
## Visualizar os resultados
ggiNEXT(resultados_repteis, type = 1) +
geom_vline(xintercept = 48, lty = 2) +
scale_linetype_discrete(labels = c("Interpolado", "Extrapolado")) +
scale_colour_manual(values = c("darkorange", "cyan4")) +
scale_fill_manual(values = c("darkorange", "cyan4")) +
labs(x = "Número de indivíduos", y = " Riqueza de espécies") +
tema_livro()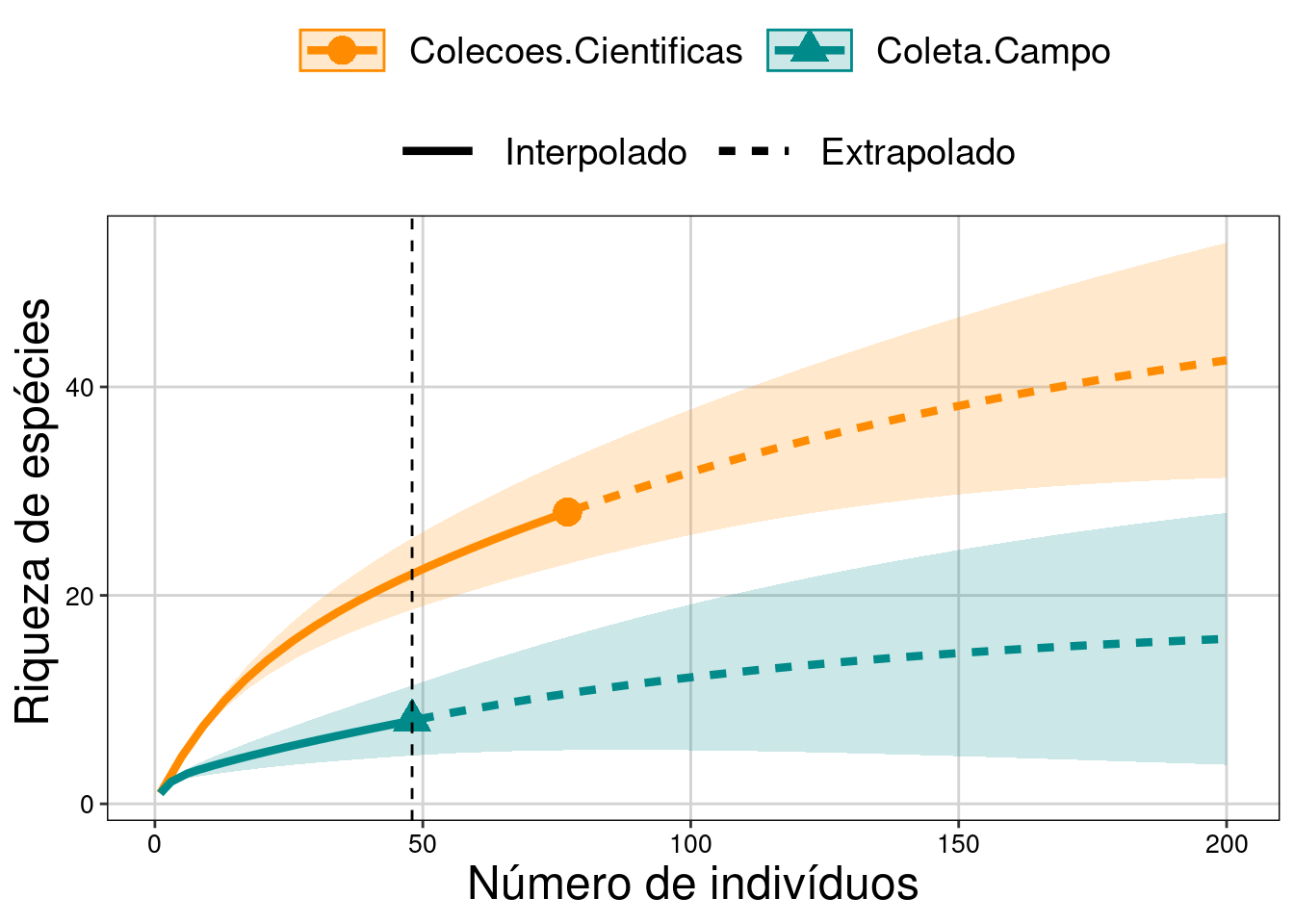
Figura 10.2: Curvas de rarefação baseada nos indivíduos de répteis.
Interpretação dos resultados
Foram registradas oito espécies de répteis nas coletas de campo (48 indivíduos) e 28 espécies nas coleções científicas (77 indivíduos). Com base na rarefação, concluímos que a riqueza de espécies de répteis obtida nas coleções científicas (20,5) é 2,5 vezes maior do que a obtida em coletas de campo.
Olhando os dados dos anuros.
## Cabeçalho
head(rarefacao_anuros)
#> Coleta.Campo Colecoes.Cientificas
#> Chiasmocleis_albopunctata 15 0
#> Dendropsophus_elianae 11 1
#> Dendropsophus_jimi 15 2
#> Dendropsophus_nanus 0 1
#> Dendropsophus_minutus 24 0
#> Dendropsophus_sanborni 0 1Análise e visualização do gráfico (Figura 10.3).
## Análise
resultados_anuros <- iNEXT(rarefacao_anuros, q = 0,
datatype = "abundance", endpoint = 800)
## Visualizar os resultados
ggiNEXT(resultados_anuros, type = 1) +
geom_vline(xintercept = 37, lty = 2) +
scale_linetype_discrete(labels = c("Interpolado", "Extrapolado")) +
scale_colour_manual(values = c("darkorange", "cyan4")) +
scale_fill_manual(values = c("darkorange", "cyan4")) +
labs(x = "Número de indivíduos", y = " Riqueza de espécies") +
tema_livro()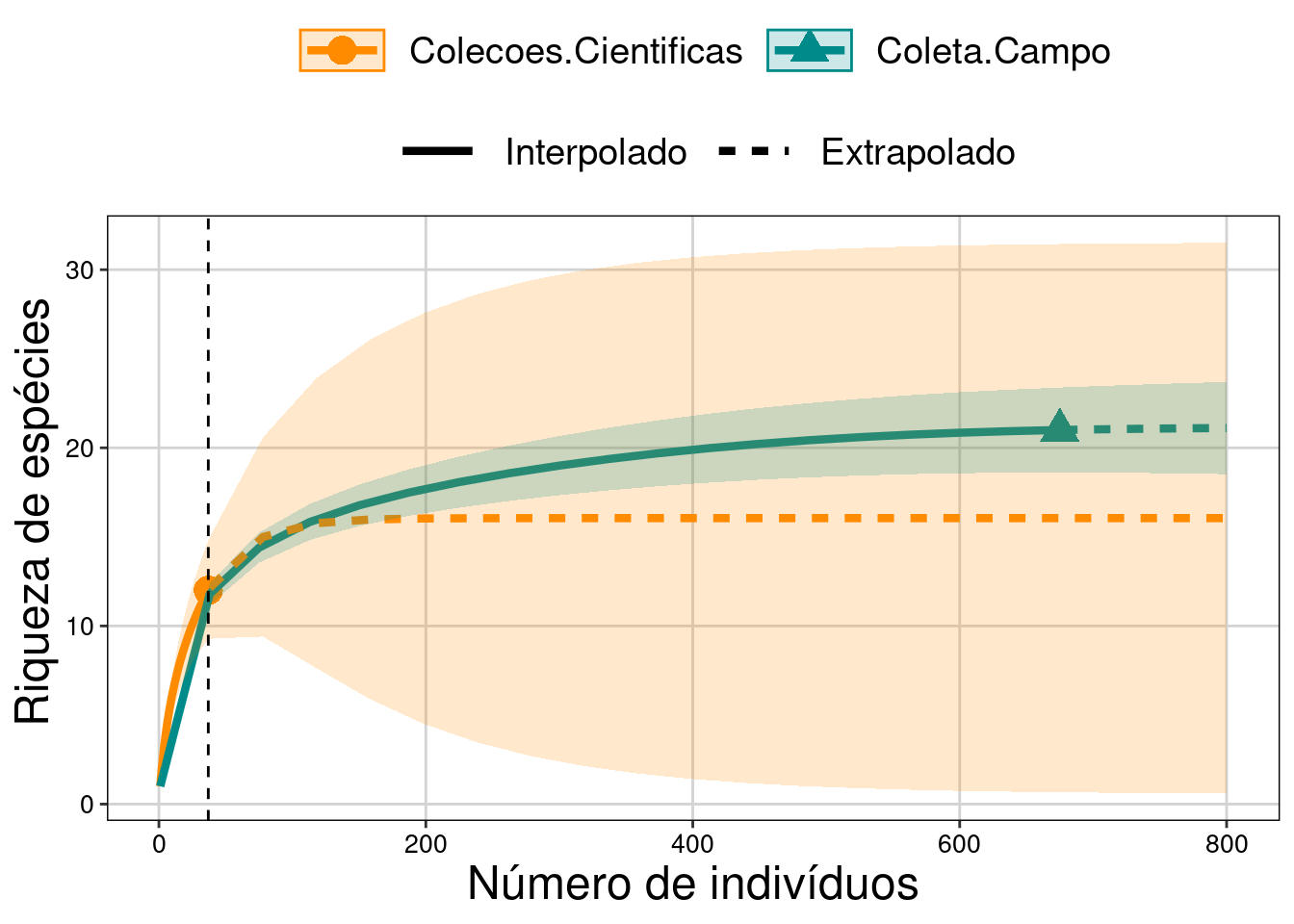
Figura 10.3: Curvas de rarefação baseada nos indivíduos de anuros.
Interpretação dos resultados - anuros
Foram registradas 21 espécies de anuros nas coletas de campo (675 indivíduos) e 12 espécies nas coleções científicas (37 indivíduos). Com base na rarefação, concluímos que não há diferença entre a riqueza de espécies de anuros obtida em coletas de campo e coleções científicas.
10.3 Curva de rarefação baseada em amostras (sample-based)
Exemplo prático 3 - Morcegos
Explicação dos dados
Usaremos os mesmos dados de espécies de morcegos amostradas em três fragmentos florestais (Breviglieri 2008). Contudo, ao invés de padronizarmos a riqueza de espécies pela abundância, iremos padronizar pelo número de amostras.
Variáveis
- Lista de vetores. Cada vetor deve conter como primeira informação o número total de amostras (variável preditora), seguido da frequência de ocorrência das espécies (i.e. número de amostras em que cada espécie foi registrada - variável resposta)
Checklist
- Verificar se sua lista está com o número total de amostras e a frequência de ocorrência das espécies
Análise
Vamos olhar os dados.
## Cabeçalho
head(dados_amostras)
#> MC_Tenentes MC_Talhadinho FF_Experimental
#> amostras 12 20 12
#> sp1 12 20 12
#> sp2 12 19 10
#> sp3 10 15 8
#> sp4 8 10 8
#> sp5 6 7 7Vamos criar uma lista com as amostragens de cada comunidade e os códigos da análise.
## Dados
# Usamos [,] para excluir os NAs. Lembrando que valores antes da
# vírgula representam as linhas e os posteriores representam as colunas.
lista_rarefacao <- list(Tenentes = dados_amostras[1:18, 1],
Talhadinho = dados_amostras[, 2],
Experimental = dados_amostras[1:16, 3])
## Análise
res_rarefacao_amostras <- iNEXT(lista_rarefacao, q = 0,
datatype = "incidence_freq")Visualizar os resultados (Figura 10.4).
## Gráfico
ggiNEXT(res_rarefacao_amostras , type = 1, color.var = "site") +
geom_vline(xintercept = 12, lty = 2) +
scale_linetype_discrete(name = "Método", labels = c("Interpolado", "Extrapolado")) +
scale_colour_manual(values = c("darkorange", "darkorchid", "cyan4")) +
scale_fill_manual(values = c("darkorange", "darkorchid", "cyan4")) +
labs(x = "Número de amostras", y = " Riqueza de espécies") +
tema_livro()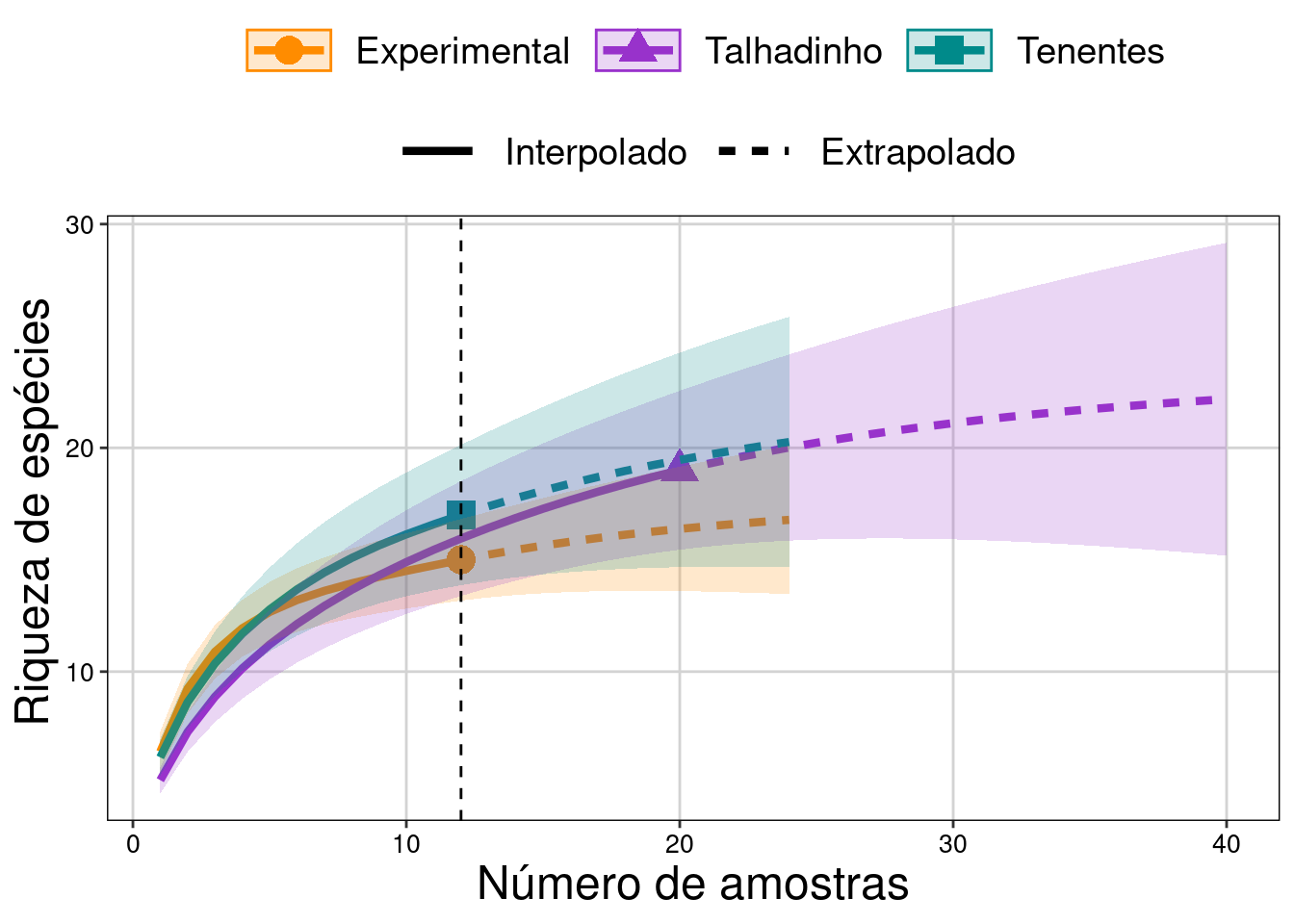
Figura 10.4: Curvas de rarefação baseada em amostras de morcegos.
Interpretação dos resultados
Olhando o gráfico é possível perceber que a riqueza de espécies de morcegos rarefeita não é diferente entre os três fragmentos florestais, quando corrigimos o problema da diferença no número de amostras.
10.4 Curva de rarefação coverage-based
Exemplo prático 4 - Morcegos
Explicação dos dados
Neste exemplo, usaremos os mesmos dados de espécies de morcegos amostradas em três fragmentos florestais (Breviglieri 2008).
Análise
Os códigos para a realização da rarefação coverage-based são idênticos aos utilizados para o cálculo das curvas de rarefações baseadas nas abundâncias e amostras. Portanto, não repetiremos as linhas de código aqui e utilizaremos os resultados já calculados para a visualização dos gráficos. Para isso, digitamos type = 3 que representa a curva de rarefação coverage-based (Figura 10.5).
## Gráfico
# Visualizar os resultados da rarefação *coverage-based*.
ggiNEXT(res_rarefacao_amostras, type = 3, color.var = "site") +
geom_vline(xintercept = 0.937, lty = 2) +
scale_linetype_discrete(labels = c("Interpolado", "Extrapolado")) +
scale_colour_manual(values = c("darkorange", "darkorchid", "cyan4")) +
scale_fill_manual(values = c("darkorange", "darkorchid", "cyan4")) +
labs(x = "Representatividade nas amostras", y = "Riqueza de espécies") +
tema_livro()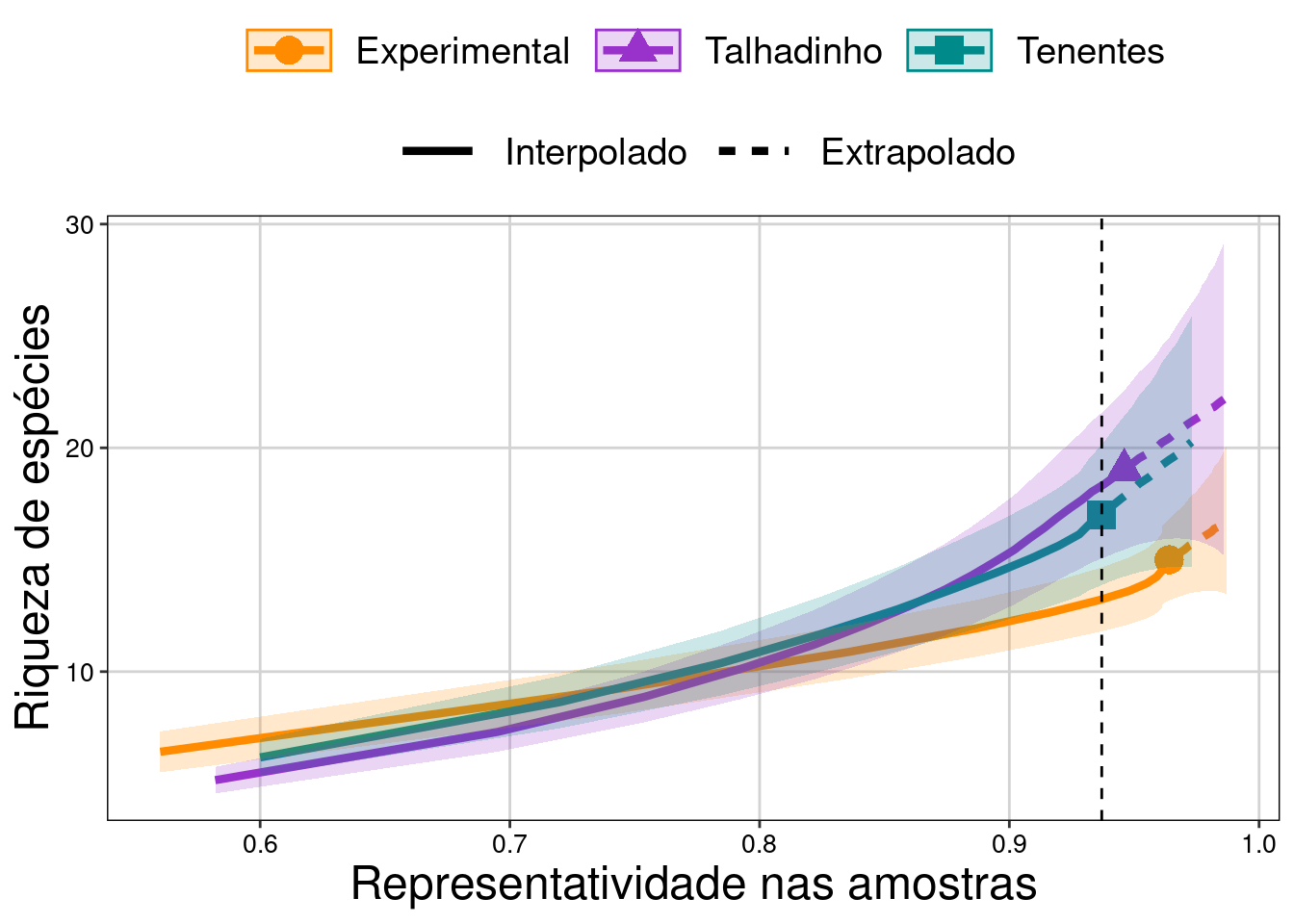
Figura 10.5: Curvas de rarefação baseada coverage-based de morcegos.
Interpretação dos resultados
Coverage é uma medida que determina a proporção de amostras (sampled-based) ou do número de indivíduos (abundance-based) da comunidade que representa as espécies presentes na amostra. Um valor de coverage = 0,85 representa a riqueza estimada com base em 85% das amostragens ou da abundância da comunidade. No nosso exemplo, os valores de coverage foram acima de 0,93, indicando que precisamos de praticamente todas as amostras para estimar a riqueza observada em cada comunidade. Comparando as comunidades considerando o mesmo valor de coverage 0,937 na comunidade Tenentes, identificamos que a riqueza de espécies de morcegos estimada na comunidade Experimental é menor do que a estimada para a comunidade de Talhadinho (não há sobreposição do intervalo de confiança). Percebam que usando a curva de rarefação coverage-based, a interpretação dos resultados foi diferente das observadas usando as curvas baseadas nos indivíduos ou amostras. Veja Chao & Jost (2012) e Roswell et al. (2021) para explicações mais detalhadas sobre esta metodologia.
Exemplo prático 5 - Generalized Least Squares (GLS)
Explicação dos dados
Neste exemplo, iremos refazer o exercício do Capítulo 7 onde usamos Generalized Least Squares (GLS) para testar a relação da riqueza de ácaros com a quantidade de água no substrato. Contudo, ao invés de considerar a riqueza de espécies de ácaros observada como variável resposta, iremos utilizar a riqueza rarefeita para controlar o efeito da amostragem (i.e. diferentes abundâncias entre as comunidades). Os dados que usaremos estão disponíveis no pacote vegan e representam a composição de espécies de ácaros amostradas em 70 amostras.
Pergunta
- A riqueza rarefeita de espécies de ácaros é maior em comunidades localizadas em áreas com substratos secos?
Predições
- O número de espécies rarefeita será maior em substratos secos, uma vez que as limitações fisiológicas impostas pela umidade limitam a ocorrência de várias espécies de ácaros
Variáveis
- Matriz ou data frame com as abundâncias das espécies de ácaros (variável resposta) registradas em 70 comunidades (variável preditora)
Checklist
- Verificar se a sua matriz ou data frame estão com as espécies nas linhas e as comunidades nas colunas
Análise
Vamos calcular a riqueza rarefeita com base na comunidade com menor abundância.
## Menos abundância
# Os dados estão com as comunidades nas colunas e as espécies nas linhas.
# Para as análises teremos que transpor a planilha.
composicao_acaros <- as.data.frame(t(mite))
# Verificar qual é a menor abundância registrada nas comunidades.
abun_min <- min(colSums(composicao_acaros))Vamos calcular a riqueza rarefeita de espécies para todas as comunidades considerando a menor abundância.
Para padronizar e facilitar a extração dos resultados, definimos os argumentos knots (i.e. representa o intervalo igualmente espaçado que a função irá utilizar para determinar a riqueza estimada) e endpoint (i.e. o valor final de amostras ou abundância extrapolados) com o valor de abundância = 8.
## Riqueza rarefeita
resultados_rarefacao <- iNEXT(composicao_acaros,
q = 0,
datatype = "abundance",
knots = abun_min,
endpoint = abun_min)Lembrando, estamos interessados no valor rarefeito considerando a abundância de 8 indivíduos. Esta informação está armazenada na linha 8 e na coluna 4 dos data frames salvos no objeto resultados_rarefação$iNextEst. Assim, para obtermos o valor rarefeito de interesse, vamos criar um loop for para facilitar a extração da riqueza rarefeita para as 70 comunidades.
## Riqueza rarefeita para cada comunidade
riqueza_rarefeita <- c()
for (i in 1:70) {
resultados_comunidades <- resultados_rarefacao$iNextEst[[i]]
subset_res <- resultados_comunidades %>% dplyr::filter(m==abun_min)
riqueza_rarefeita[i] <- subset_res$qD
}Vamos juntar esses resultados com os dados geográficos e ambientais.
## Dados finais
# Agrupando os dados em um data frame final.
dados_combinado <- data.frame(riqueza_rarefeita, agua, coord)Agora, seguindo os passos descritos no Capítulo 7, vamos identificar o melhor modelo que representa a estrutura espacial dos dados da riqueza rarefeita.
## Criando diferentes modelos usando a função gls
## Sem estrutura espacial
no_spat_gls <- gls(riqueza_rarefeita ~ agua, data = dados_combinado,
method = "REML")
## Covariância esférica
espher_model <- gls(riqueza_rarefeita ~ agua, data = dados_combinado,
corSpher(form = ~lat + long, nugget = TRUE))
## Covariância exponencial
expon_model <- gls(riqueza_rarefeita ~ agua, data = dados_combinado,
corExp(form = ~lat + long, nugget = TRUE))
## Covariância Gaussiana
gauss_model <- gls(riqueza_rarefeita ~ agua, data = dados_combinado,
corGaus(form = ~lat + long, nugget = TRUE))
## Covariância razão quadrática
ratio_model <- gls(riqueza_rarefeita ~ agua, data = dados_combinado,
corRatio(form = ~lat + long, nugget = TRUE))Agora vamos usar a seleção de modelo por AIC para selecionar o modelo mais “provável” explicando a distribuição da riqueza rarefeita das espécies de ácaros (Figura 10.6).
## Seleção dos modelos
aic_fit <- AIC(no_spat_gls, espher_model, expon_model,
gauss_model, ratio_model)
aic_fit %>% arrange(AIC)
#> df AIC
#> 1 5 164.5840
#> 2 5 165.7649
#> 3 5 165.8698
#> 4 3 166.7530
#> 5 5 169.0242
## Visualizando os resíduos do modelo selecionado
plot(gauss_model)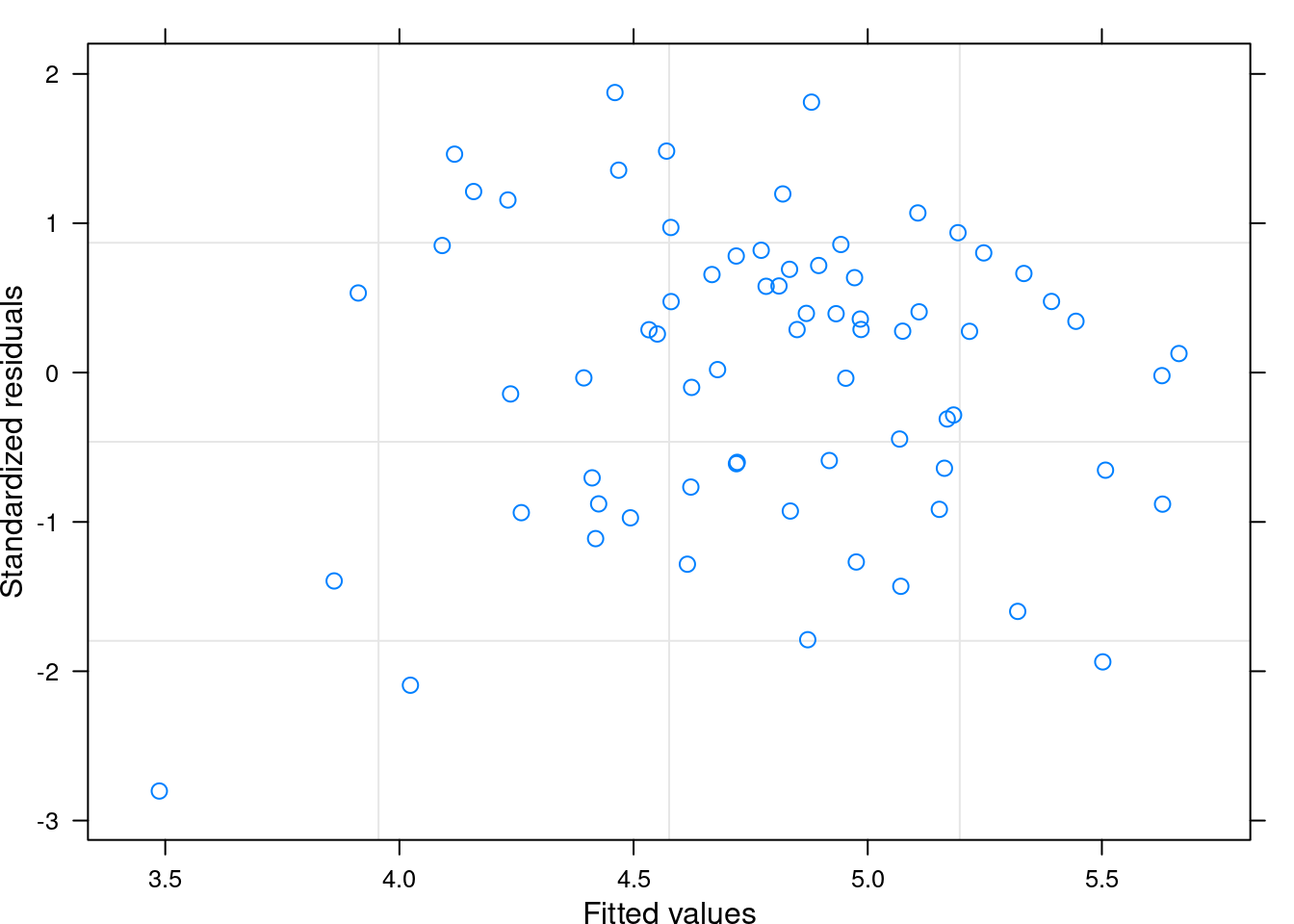
Figura 10.6: Visualização dos resíduos do modelo selecionado.
Percebam que os pontos estão dispersos no gráfico e não apresentam padrões que indiquem heterogeneidade de variância (Figura 10.7).
## Visualizando os resultados
summary(gauss_model)$tTable
#> Value Std.Error t-value p-value
#> (Intercept) 6.086125990 0.2927633291 20.788553 3.550849e-31
#> agua -0.003142615 0.0006670097 -4.711498 1.258304e-05
## Calculando o R-squared
rsquared(gauss_model)
#> Response family link method R.squared
#> 1 riqueza_rarefeita gaussian identity none 0.2991059
## Obtendo os valores preditos pelo modelo
predito <- predict(gauss_model)
## Plotando os resultados no gráfico
ggplot(data = dados_combinado, aes(x= agua, y= riqueza_rarefeita)) +
geom_point(size = 4, shape = 21, fill = "gray", alpha = 0.7) +
geom_line(aes(y = predito), size = 1) +
labs(x = "Concentração de água no substrato",
y = "Riqueza rarefeita \ndas espécies de ácaros") +
tema_livro()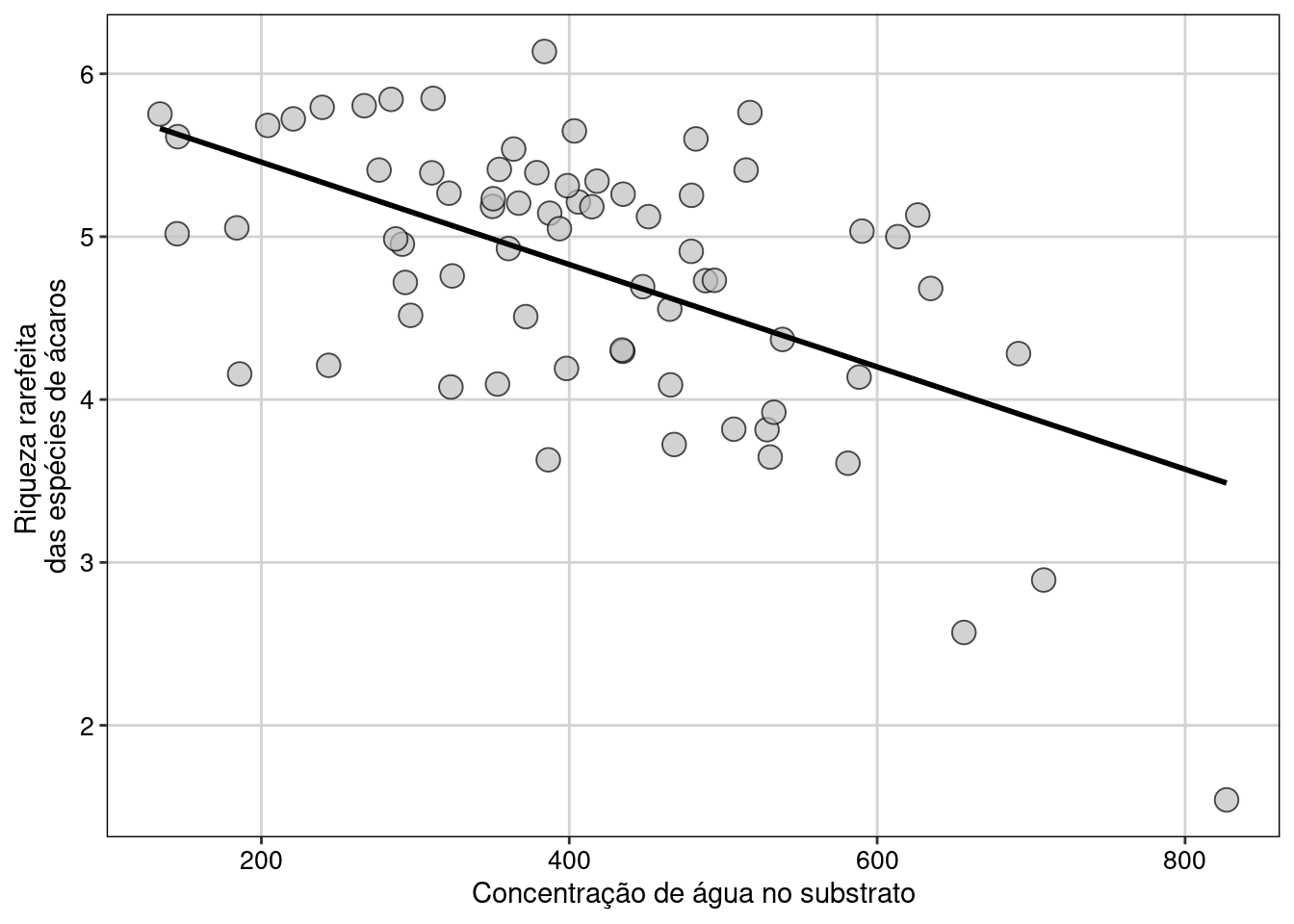
Figura 10.7: Gráfico do modelo GLS selecionado.
Interpretação dos resultados
A concentração de água no substrato explica 29,9% da variação na riqueza rarefeita das espécies de ácaros. Como predito, a riqueza de espécies de ácaros foi maior em comunidades localizadas em áreas com substratos secos do que em áreas com substratos úmidos (t = -4.71, df = 68, P < 0.01).
10.5 Para se aprofundar
10.5.1 Livros
- Recomendamos o livro Biological Diversity Frontiers in Measurement and Assessment (Magurran and McGill 2011)
10.5.2 Links
Recomendamos também que acessem a página do EstimateS software e baixem o manual do usuário que contém informações detalhadas sobre os índices de rarefação. Este site foi criado e é mantido pelo Dr. Robert K. Colwell, um dos maiores especialistas do mundo em estimativas da biodiversidade
Recomendamos a página pessoal da pesquisadora Anne Chao que é uma das responsáveis pelo desenvolvimento da metodologia e do pacote
iNEXT. Nesta página, vocês irão encontrar exemplos e explicações detalhadas sobre as análises
10.6 Exercícios
10.1
Usando os dados Cap10_exercicio1 disponível no pacote ecodados, avalie se diferentes tipos de uso da terra (fragmento florestal, borda de mata, área de pastagem e cana de açúcar) apresentam diferentes riquezas de espécies? Qual a sua interpretação? Faça um gráfico com os resultados.
10.2 O estudo é o mesmo do exercício anterior. Contudo, ao invés da rarefação baseada na abundância, faça rarefações baseadas no número de amostras. Qual a sua interpretação considerando os resultados do exercício 1? Faça um gráfico com os resultados.
10.3 Use os dados dos exercícios anteriores e calcule a rarefação baseada na cobertura de amostragem (coverage-based). Qual a sua interpretação considerando os resultados anteriores? Faça um gráfico com os resultados.