Capítulo 13 Diversidade Filogenética
Pré-requisitos do capítulo
Pacotes e dados que serão utilizados neste capítulo.
## Pacotes
library(devtools)
library(ecodados)
library(V.PhyloMaker)
library(vegan)
library(ggplot2)
library(GGally)
library(ggpubr)
library(picante)
library(phytools)
library(ape)
library(geiger)
library(phyloregion)
library(pez)
library(reshape2)
library(betapart)
## Dados
minha_arvore <- ecodados::filogenia_aves
especies_plantas <- ecodados::sp_list
comunidade <- ecodados::comm
composicao_especies <- ecodados::composicao_aves_filogenetica
filogenia_aves <- ecodados::filogenia_aves
precipitacao <- precipitacao_filogenetica13.1 Aspectos teóricos
A diversidade filogenética captura a ancestralidade compartilhada entre as espécies em termos de quantidade da história evolutiva e o grau de parentesco entre as espécies. Pesquisadores têm utilizado diferentes métricas de diversidade filogenética em duas linhas de investigações principais: i) incorporar a história evolutiva das espécies na seleção das áreas prioritárias para conservação visando minimizar a perda da diversidade evolutiva (Vane-Wright, Humphries, and Williams 1991; Faith 1992; Véron et al. 2019), e ii) produzir explicações sobre os processos atuando na montagem das comunidades (Webb et al. 2002; Helmus et al. 2007). A quantidade de artigos abordando ecologia, macroecologia e conservação com diversidade filogenética cresceram exponencialmente nas últimas décadas (Véron et al. 2019). Seguindo esta tendência, o número de métricas de diversidade filogenética propostas não param de aumentar. Tucker et al. (2017) revisaram 70 métricas de diversidade filogenética e classificaram estas métricas em três dimensões: i) riqueza - representa a soma da diferença filogenética acumulada entre táxons, ii) divergência - representa o padrão de diferença filogenética entre táxons de uma assembleia, e iii) regularidade - representa o grau de variação das diferenças filogenéticas entre táxons em uma assembleia. Outros autores utilizaram diferentes classificações (Pavoine and Bonsall 2011; Vellend et al. 2011; Garamszegi 2014). Neste capítulo, iremos seguir a classificação de Tucker et al. (2017) e mostrar algumas das principais métricas dentro de cada uma dessas dimensões.
📝 Importante
Alguns autores recomendam que os pesquisadores não foquem em apenas uma dimensão, mas comparem métricas de diferentes dimensões (Tucker et al. 2017).
13.2 Manipulação de filogenias
Nesta seção, iremos descrever os códigos em R para carregar, plotar, acessar os dados, e excluir e adicionar espécies em filogenias. Estes são códigos introdutórios e necessários para realizarmos as análises de diversidade filogenética. Não iremos descrever os comandos necessários para construir uma filogenia. Estamos assumindo que já existe uma filogenia disponível para os organismos de interesse.
Mas antes, vamos entender as principais terminologias de uma filogenia e analisá-las graficamente (Figura 13.1).
Árvore filogenética: são hipóteses que representam a relação de parentesco entre as espécies (pode ser também indivíduos, genes, etc.) com informações sobre quais espécies compartilham um ancestral comum e a distância (tempo, genética, ou diferenças nos caracteres) que as separam
Nó: o ponto onde uma linhagem dá origem a duas ou mais linhagens descendentes
Politomia: três ou mais linhagens descendendo de um único nó
Ramo: uma linha orientada ao longo de um eixo terminais-raiz que conecta os nós na filogenia
Terminal (do inglês tip): o final do ramo representando uma espécie atual ou extinta (pode também representar gêneros, indivíduos, genes, etc.)
Raiz: representa o ancestral comum de todas as espécies na filogenia
Clado: um grupo de espécies aparentadas descendendo de um único nó na filogenia
Ultramétrica: a distância de todos os terminais até a raiz são idênticas. Característica requerida pela maioria dos índices de diversidade filogenética
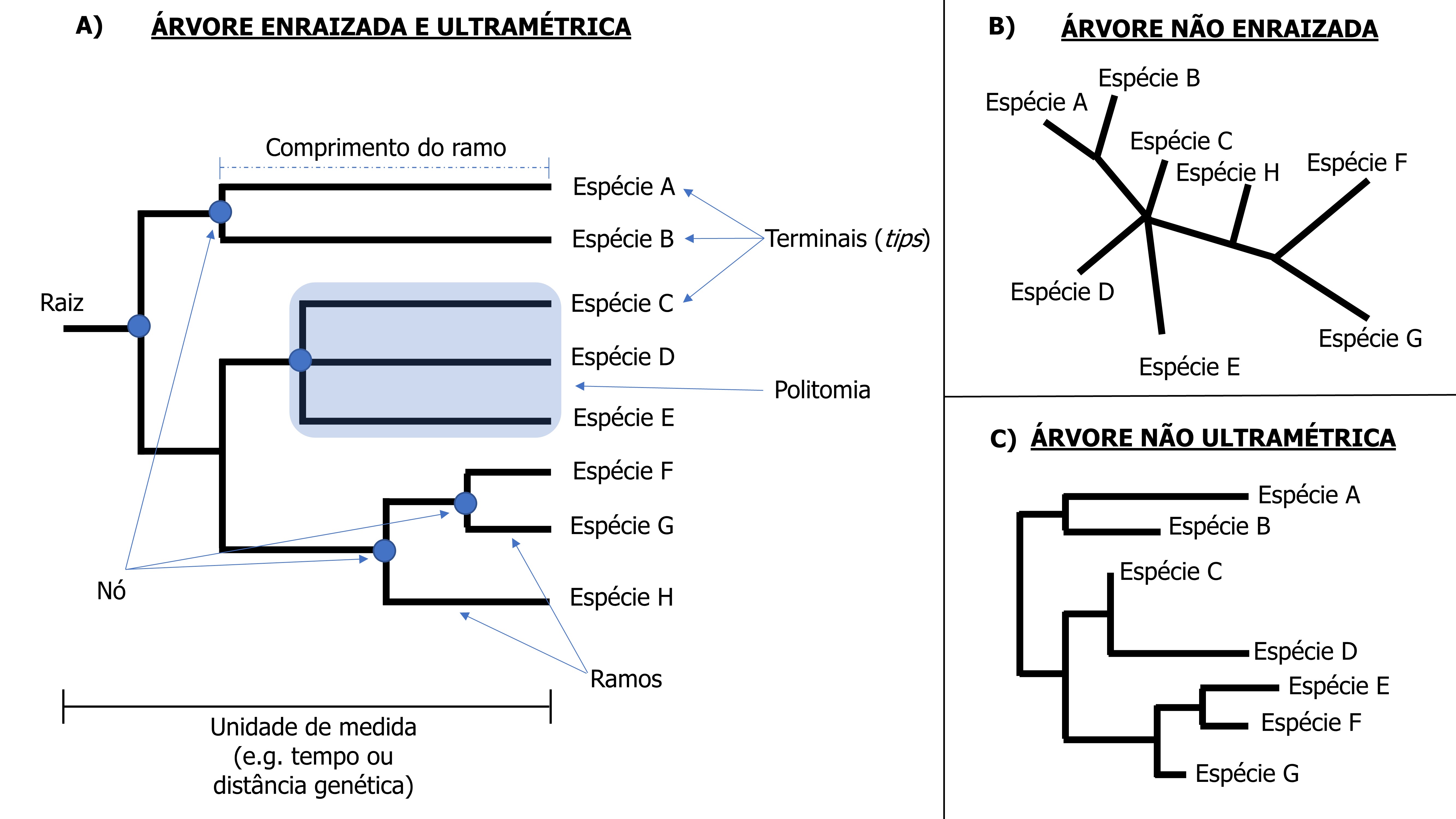
Figura 13.1: Ilustrações de diferentes árvores filogenéticas. A) Árvore enraizada e ultramétrica indicando a raiz da árvore, nós, ramos, comprimento do ramo, politomias e terminais. B) Árvore não enraizada que mostra as relações entre as espécies, mas não define a história evolutiva. C) Árvore não ultramétrica onde as espécies apresentam diferentes distâncias até a raiz.
Agora vamos plotar a filogenia para visualizar as relações entre as 37 espécies de aves endêmicas da Mata Atlântica. Essa filogenia foi extraída de Jetz et al. (2012). Os dados estão disponíveis no pacote ecodados (Figura 13.2).
## Gráfico
plot.phylo (minha_arvore, type = "phylogram", show.tip.label = TRUE,
show.node.label = TRUE, edge.color = "black", edge.width = 1.5,
tip.color = "black", cex = 0.45, label.offset = 2) 
Figura 13.2: Filogenia de 37 espécies de aves endêmicas da Mata Atlântica.
Podemos alterar o formato de apresentação da filogenia usando o argumento type e a cor dos ramos usando o argumento edge.color (Figura 13.3).
## Gráfico
plot.phylo (minha_arvore, type = "fan", show.tip.label = TRUE,
show.node.label = TRUE, edge.color = "blue", edge.width = 1.5,
tip.color = "black", cex = 0.45, label.offset = 2) 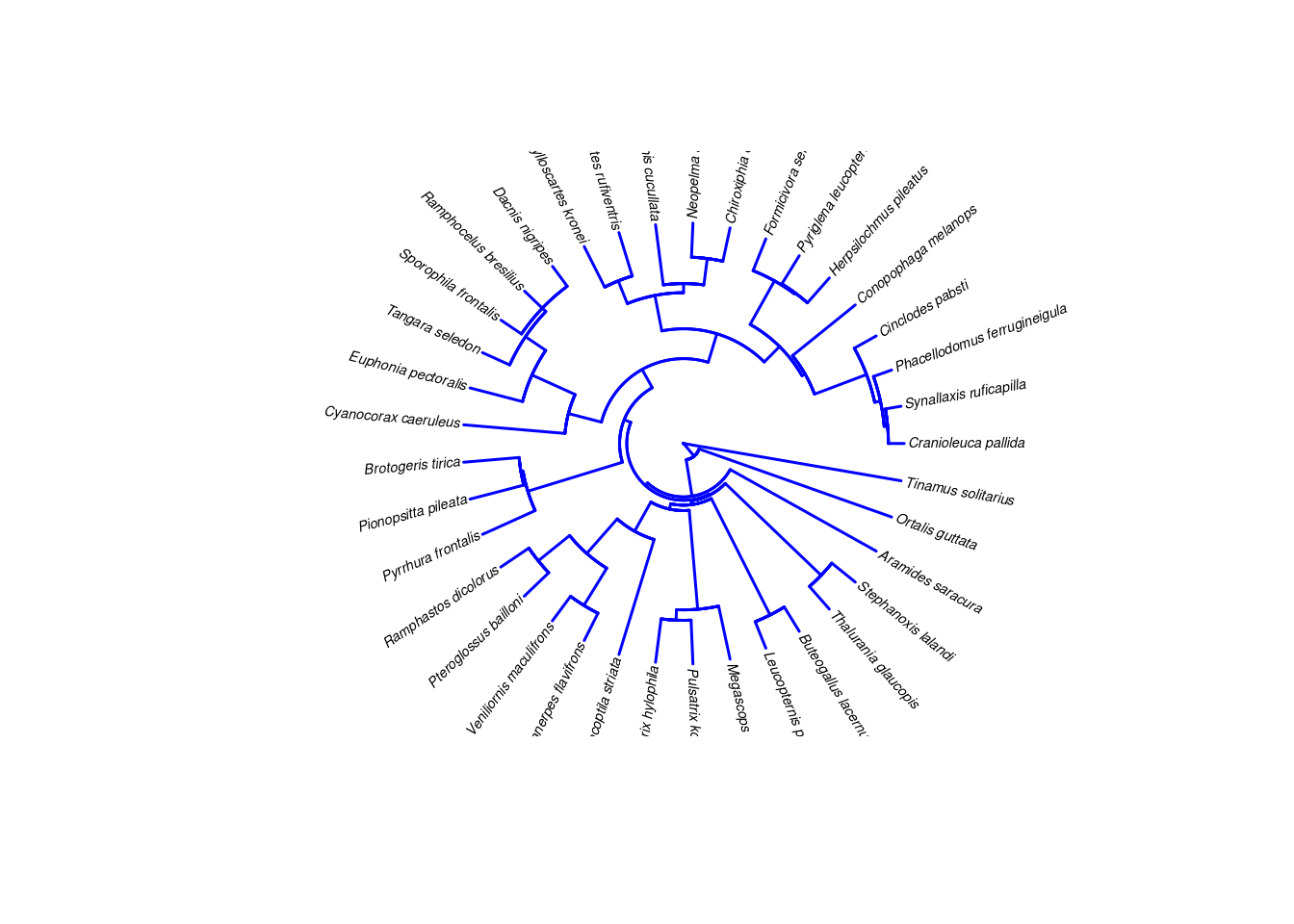
Figura 13.3: Filogenia de 37 espécies de aves endêmicas da Mata Atlântica, com alterações de parametros de visualização.
Percebam que existem vários argumentos para modificar a largura e cor dos ramos, tamanho da fonte, distância entre a filogenia e os nomes das espécies e muito mais. Uma sugestão é visitar o blog do professor Liam Revell (http://blog.phytools.org/) que é o criador e mantenedor do pacote phytools no R.
Acessar informações da filogenia
Uma das características mais interessantes do R é que podemos acessar as informações do objeto que contém a filogenia. Neste caso, o nosso objeto é a filogenia e, muitas vezes, temos interesse nas informações que estão inseridas dentro da filogenia. Para sabermos quais são as informações que podemos acessar na filogenia, vamos usar a função names().
## Nomes
names(minha_arvore)
#> [1] "edge" "edge.length" "Nnode" "tip.label"Temos acesso a quatro componentes da filogenia: i) ramo (edge), ii) comprimento do ramo (edge.length), iii) número de nós (Nnode), e iv) nome das espécies (tip.label). Podemos usar o operador $ para acessar estes componentes. Veja abaixo como acessar o nome das 37 espécies de aves na filogenia ou o comprimento de cada um dos ramos da filogenia.
## Nome das espécies
minha_arvore$tip.label
#> [1] "Cranioleuca_pallida" "Synallaxis_ruficapilla" "Phacellodomus_ferrugineigula" "Cinclodes_pabsti"
#> [5] "Conopophaga_melanops" "Herpsilochmus_pileatus" "Pyriglena_leucoptera" "Formicivora_serrana"
#> [9] "Chiroxiphia_caudata" "Neopelma_aurifrons" "Carpornis_cucullata" "Mionectes_rufiventris"
#> [13] "Phylloscartes_kronei" "Dacnis_nigripes" "Ramphocelus_bresilius" "Sporophila_frontalis"
#> [17] "Tangara_seledon" "Euphonia_pectoralis" "Cyanocorax_caeruleus" "Brotogeris_tirica"
#> [21] "Pionopsitta_pileata" "Pyrrhura_frontalis" "Ramphastos_dicolorus" "Pteroglossus_bailloni"
#> [25] "Veniliornis_maculifrons" "Melanerpes_flavifrons" "Malacoptila_striata" "Strix_hylophila"
#> [29] "Pulsatrix_koeniswaldiana" "Megascops_sanctaecatarinae" "Leucopternis_polionotus" "Buteogallus_lacernulatus"
#> [33] "Thalurania_glaucopis" "Stephanoxis_lalandi" "Aramides_saracura" "Ortalis_guttata"
#> [37] "Tinamus_solitarius"
## Comprimento dos ramos
minha_arvore$edge.length
#> [1] 8.3802647 18.8669712 1.7333865 3.6642170 10.6732942 15.2239228 11.0917270 1.7755983 28.3607791 2.9678911 1.7546545
#> [12] 8.0910030 8.0910030 9.8456576 12.8135486 41.1743278 25.4606915 0.5546030 16.9346316 16.9346316 17.4892346 18.4363079
#> [23] 4.6581580 13.5498048 17.3960309 17.3960309 30.9471871 12.4567724 23.1472214 23.1472214 17.4065182 24.1723764 12.4712971
#> [34] 2.4600303 12.6082491 12.5529673 12.6146793 15.2153841 27.6866812 51.8590576 50.4721698 1.0975337 28.3691666 28.3691666
#> [45] 29.4667004 0.4805624 1.9967144 2.7687118 17.0272986 23.4955884 20.5338341 17.3003772 17.3003772 22.2636579 15.5705534
#> [56] 15.5705534 61.3297997 50.6621138 5.3479249 22.3470597 22.3470597 27.6949846 66.5513507 14.5744595 14.5744595 67.7448719
#> [67] 15.3776527 15.3776527 85.3364736 104.2034448 112.5837095Remover espécies da filogenia
Nas análises de diversidade filogenética, as espécies que estarão presentes na filogenia normalmente são aquelas que foram amostradas no seu estudo. Contudo, muitas vezes utilizamos filogenias contendo espécies que não estão presentes no nosso estudo. Neste caso, precisamos excluir essas espécies da filogenia. A função drop.tip() faz essa tarefa.
## Remover espécies da filogenia
# Vamos criar um novo nome para o objeto e excluir as espécies Leucopternis polionotus e Aramides saracura da filogenia
filogenia_cortada <- drop.tip(minha_arvore, c("Leucopternis_polionotus", "Aramides_saracura"))
filogenia_cortada
#>
#> Phylogenetic tree with 35 tips and 33 internal nodes.
#>
#> Tip labels:
#> Cranioleuca_pallida, Synallaxis_ruficapilla, Phacellodomus_ferrugineigula, Cinclodes_pabsti, Conopophaga_melanops, Herpsilochmus_pileatus, ...
#>
#> Rooted; includes branch lengths.Vejam que agora a filogenia tem 35 espécies de aves. As duas espécies que selecionamos foram excluídas da filogenia.
Adicionar espécies na filogenia
Outra situação bem comum é quando precisamos inserir espécies que foram amostradas no nosso estudo, mas não estão presente na filogenia. Para isso, vamos usar a função add.species.to.genus(). A função force.ultrametric() é usada para que a filogenia continue sendo ultramétrica (sem essa função a árvore perde os comprimentos dos ramos)
📝 Importante
O comprimento do ramo que a espécie irá receber dependerá de onde você indicar a inserção da espécie.
As opções são:
- root: insere a espécie no ancestral comum mais recente (MRCA) de todas as espécies do gênero (default)
- random: insere a espécie aleatoriamente dentro do clado do MRCA contendo todos as espécies do gênero
## Adicionar espécies à filogenia
# Vamos inserir as espécies Megascops_sp1, Carponis_sp, Strix_sp1, Strix_sp2 e
# Strix_sp3 na filogenia
Megascops <- c("Megascops_sp1")
Carpornis <- c("Carpornis_sp1")
Strix <- c("Strix_sp1", "Strix_sp2", "Strix_sp3")
# Inserindo espécies como politomias
filogenia_nova <- add.species.to.genus(force.ultrametric(minha_arvore, message = FALSE), Megascops)
filogenia_nova <- add.species.to.genus(force.ultrametric(filogenia_nova, message = FALSE), Carpornis)Agora vamos inserir várias espécies dentro do mesmo gênero.
## Adicionar várias espécies à filogenia
# Para inserir mais de uma espécie dentro do gênero, vamos utilizar um loop.
for(i in 1:length(Strix))
filogenia_nova <- add.species.to.genus(force.ultrametric(filogenia_nova, message = FALSE),
Strix[i], where = "root")Vamos plotar essa nova filogenia (Figura 13.4).
## Gráfico
plot(filogenia_nova, cex = 0.5, no.margin = TRUE)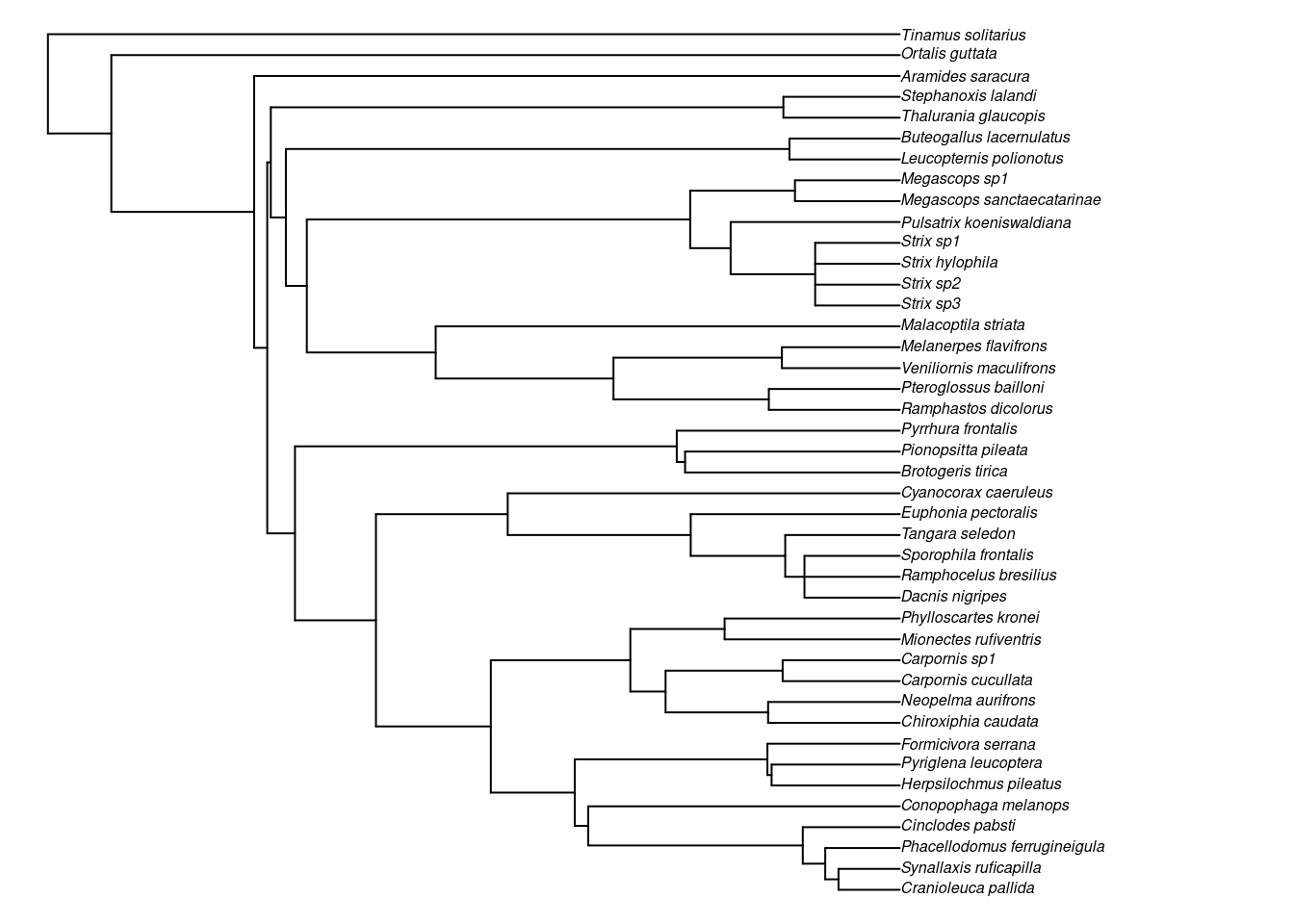
Figura 13.4: Filogenia de espécies de aves endêmicas da Mata Atlântica, com adição de espécies.
Vamos fazer outro exemplo usando a função phylo.maker() do pacote V.PhyloMaker que adiciona as espécies nos gêneros ou os gêneros nas famílias usando uma filogênia backbone.
Essa função permite a adição dos gêneros ou espécies considerando três cenários diferentes:
- Cenário 1: adiciona gêneros ou espécies como politomias basais dentro das famílias ou gêneros da filogenia respectivamente
- Cenário 2: adiciona gêneros e espécies aleatoriamente nas famílias ou gêneros da filogenia respectivamente
- Cenário 3: adiciona gêneros e espécies nas famílias ou gêneros da filogenia respectivamente usando as abordagens implementadas no Phylomatic e BLADJ
## phylo.maker
# A função phylo.maker usa uma filogenia default de plantas (i.e. GBOTB.extended).
# Caso você queira utilizar outra filogenia, é só alterar o argumento tree
novas_filogenias <- phylo.maker(especies_plantas,
tree = GBOTB.extended,
scenarios = c("S1","S2","S3"))
#> [1] "Note: 2 taxa fail to be binded to the tree,"
#> [1] "Genus7_sp1" "Genus8_sp1"Vamos essa filogenia criada pelo pacote V.PhyloMaker (Figura 13.5).
## Gráfico
par(mfrow = c(1, 2))
plot.phylo(novas_filogenias$scenario.1, cex = 0.5, main = "Cenário 1")
plot.phylo(novas_filogenias$scenario.3, cex = 0.5, main = "Cenário 3")
dev.off()
#> null device
#> 1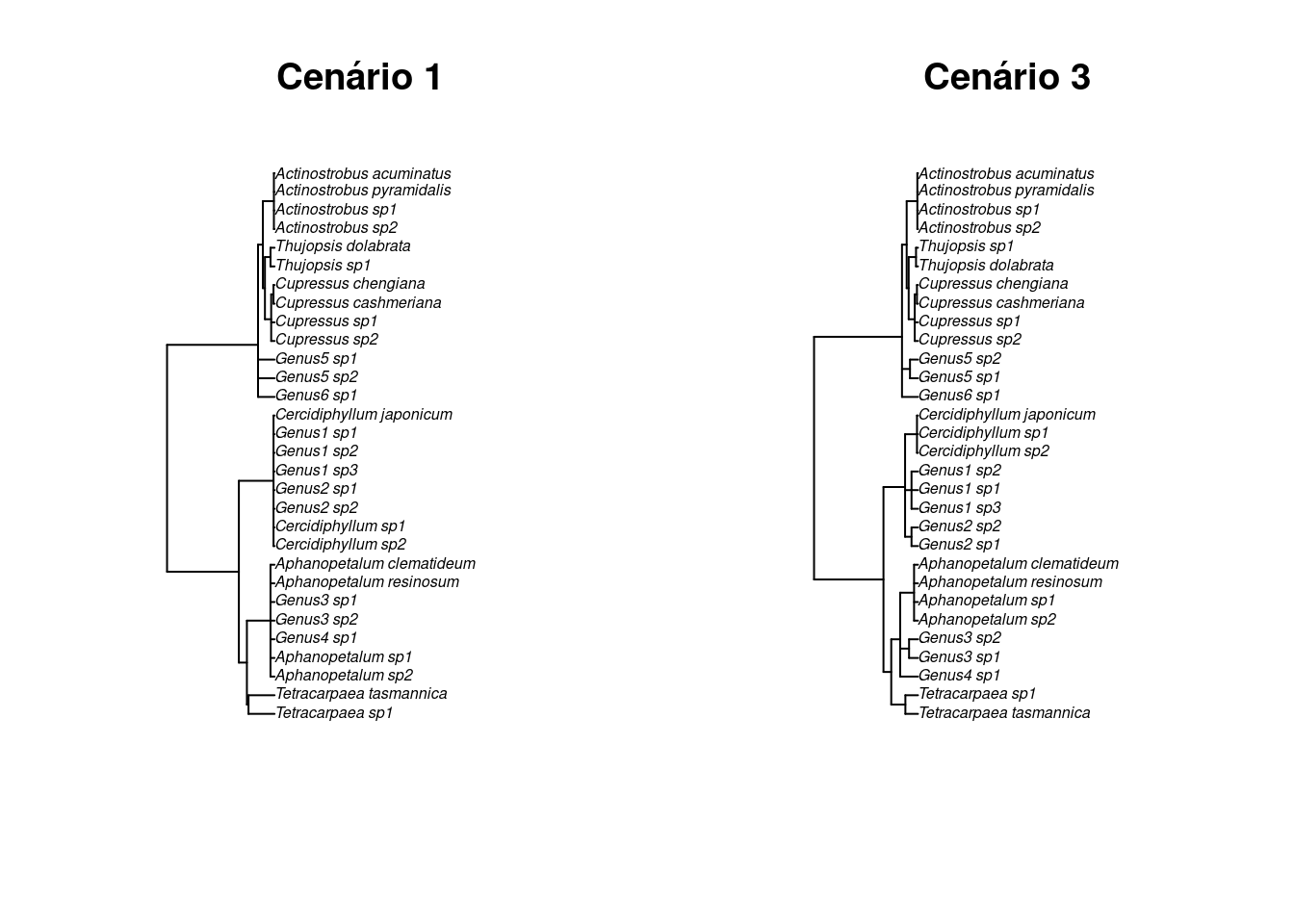
Figura 13.5: Filogenia de espécies de plantas criada pelo pacote V.PhyloMaker.
13.3 Métricas de diversidade alfa filogenética
Métricas de diversidade alfa utilizam os dados de incidência (presença e ausência) ou abundância das espécies para determinar um valor de diversidade para cada comunidade ou sítio de interesse.
Exemplo prático 1
Explicação dos dados
Avaliaremos a diversidade filogenética de 10 comunidades de aves amostradas ao longo de um gradiente de precipitação. Utilizaremos este conjunto de dados para todos os exemplos deste capítulo.
Pergunta
- A variação na distribuição espacial dos valores de diversidade filogenética das comunidades está associada com o gradiente de precipitação?
Predições
- Os valores de diversidade filogenética serão maiores nas comunidades localizadas em regiões com altas precipitações do que em regiões mais secas
Variáveis
Data frame com as comunidades (unidade amostral) nas linhas e as espécies de aves nas colunas (variável resposta)
Data frame com as comunidades (unidade amostral) nas linhas e a variável precipitação anual na coluna (variável preditora)
Arquivo com a filogenia das 37 espécies de aves (variável resposta)
Checklist
Verificar se os data frames de composição de espécies e variáveis ambientais estão com as unidades amostrais nas linhas e variáveis preditoras nas colunas
Verificar se as comunidades nos data frames de composição de espécies e variáveis ambientais estão distribuídos na mesma sequência/ordem nos dois arquivos.
Verificar se o nome das espécies de aves no data frame de composição de espécies é idêntico ao nome das espécies na filogenia.
13.3.1 Riqueza da diversidade alfa filogenética
As métricas de riqueza somam a quantidade da diferença filogenética presente em uma comunidade (Tucker et al. 2017).
Phylogenetic diversity (PD)
Esta métrica é definida pela soma do comprimento dos ramos conectando todas as espécies na comunidade. É a métrica mais conhecida e usada nos estudos de conservação e comunidade (Faith 1992).
Vamos conferir se os nomes das espécies de aves no data frame de composição são os mesmos da filogenia. O resultado OK indica que os nomes estão corretos. Caso contrário, você deve verificar e arrumar.
## Conferir os nomes das espécies
name.check(filogenia_aves, t(composicao_especies))
#> [1] "OK"Agora vamos colocar os nomes das espécies do data frame na mesma ordem que os nomes aparecem na filogenia. Isso é obrigatório para algumas funções.
## Colocar os nomes das espécies do data frame na mesma ordem que aparecem na filogenia
composicao_especies_P <- match.phylo.comm(phy = filogenia_aves, comm = composicao_especies)$commAbaixo, demonstramos os códigos no R para o cálculo de PD para as comunidades de aves.
## Phylogenetic diversity (PD)
# Calculando a métrica de diversidade filogenética proposta por Faith (1992).
resultados_PD <- pd(composicao_especies_P, filogenia_aves)
# Mostra o valor de PD e riqueza de espécies para cada comunidade.
resultados_PD
#> PD SR
#> Com_1 1259.3151 27
#> Com_2 1293.1521 26
#> Com_3 1222.3102 25
#> Com_4 1254.5410 25
#> Com_5 1021.9670 22
#> Com_6 856.7810 18
#> Com_7 930.6452 15
#> Com_8 678.9394 12
#> Com_9 673.6288 13
#> Com_10 599.6924 9A comunidade 2 abriga a maior diversidade filogenética com a composição de espécies contemplando 1293,15 milhões de anos (i.e. soma do comprimento dos ramos ligando todas as espécies da comunidade). Por outro lado, a comunidade 10 abriga a menor diversidade filogenética contemplando 599,69 milhões de anos.
📝 Importante
Este índice é correlacionado com a riqueza de espécies. Discutiremos essa questão na seção de modelos nulos.
Phylogenetic Species Richness (PSR)
Esta métrica é calculada multiplicando a riqueza de espécies registrada na comunidade pela Phylogenetic Species Variability (PSV) da comunidade (Helmus et al. 2007). PSR é diretamente comparável ao número de espécies na comunidade, mas inclui o parentesco filogenético entre as espécies.
Abaixo, demonstramos os códigos no R para o cálculo do PSR utilizando os dados das comunidades de aves.
## Phylogenetic Species Richness (PSR)
# Análise com dados de composição das espécies nas comunidades.
resultados_PSR <- psr(composicao_especies_P,filogenia_aves)
# Mostra os valores de PSR para cada comunidade.
resultados_PSR
#> PSR SR vars
#> Com_1 18.084236 27 0.04537904
#> Com_2 18.167183 26 0.04881734
#> Com_3 16.230938 25 0.05205832
#> Com_4 17.153972 25 0.05205832
#> Com_5 13.981597 22 0.06060866
#> Com_6 11.287030 18 0.06933707
#> Com_7 10.279983 15 0.07398666
#> Com_8 7.538134 12 0.07721118
#> Com_9 8.060933 13 0.07627517
#> Com_10 5.720063 9 0.07948474A comunidade 2 abriga o maior valor de PSR enquanto a comunidade 10 abriga o menor valor. Vejam que PSR é fortemente correlacionado com número de espécies nas comunidades (r = 0.99, p <0.0001). Contudo, existe uma variabilidade residual no PSR em relação ao número de espécies que afeta o ranqueamento das comunidades quando utilizando PSR ou número de espécies. Consequentemente, a escolha da métrica pode gerar diferentes delineamentos de áreas prioritárias para conservação (Helmus et al. 2007).
Phylogenetic Endemism (PE)
Esta métrica calcula a fração dos ramos restritas a regiões específicas. PE identifica áreas ou comunidades que abrigam componentes restritos da diversidade filogenética. PE é uma métrica proposta para auxiliar estudos de conservação estabelecendo critérios para priorizar regiões a serem conservadas com base na importância evolutiva (i.e. partes da filogênia com distribuição espacial limitada) das espécies que ocorrem nestes locais (Rosauer et al. 2009).
Abaixo, demonstramos os códigos no R para o cálculo do PE utilizando os dados das comunidades de aves.
## Phylogenetic Endemism (PE)
# Transformando data.frame em matriz.
dados_matriz <- as.matrix(composicao_especies_P)
# Análise.
resultados_PE <- phylo_endemism(dados_matriz, filogenia_aves,
weighted = TRUE)
# Mostra os valores de PE para cada comunidade.
resultados_PE
#> Com_1 Com_2 Com_3 Com_4 Com_5 Com_6 Com_7 Com_8 Com_9 Com_10
#> 232.09145 272.60106 210.22647 218.89037 146.99281 135.06423 148.65234 79.22402 77.95458 68.50266O índice PE considera as 10 comunidades como o range espacial máximo. Se todas as espécies ocorressem nas 10 comunidades, o valor de PE seria 1, indicando baixo endemismo filogenético. A comunidade 2 abriga um conjunto de espécies cujo os ramos com distribuição espacial restrita contemplam 272,6 milhões de anos. Por outro lado, a comunidade 10 abriga um conjunto de espécies cujo os ramos com distribuição espacial restrita contemplam 68,5 milhões de anos. Assim, as comunidades 1, 2 e 4 são as áreas que abrigam os maiores endemismo filogenéticos.
Species Evolutionary Distinctiveness (ED)
Esta métrica calcula qual é a fração da árvore filogenética que é atribuída para uma espécie. ED reflete quão evolutivamente isolada uma espécie é comparada com as outras espécies na filogenia (Redding and Mooers 2006). ED é uma métrica proposta para auxiliar estudos de conservação estabelecendo critérios para priorizar as espécies a serem conservadas com base na sua importância evolutiva (exclusividade do comprimento do ramo) que não é compartilhada com outras espécies. Portanto, apenas as informações da filogenia são utilizadas para o cálculo de ED.
Abaixo, demonstramos os códigos no R para o cálculo do ED utilizando os dados das comunidades de aves.
## Species Evolutionary Distinctiveness (ED)
# Análise.
resultados_ED <- evol.distinct(filogenia_aves)
# Mostra os valores de ED para cada espécie.
head(resultados_ED)
#> Species w
#> 1 Cranioleuca_pallida 14.07447
#> 2 Synallaxis_ruficapilla 14.07447
#> 3 Phacellodomus_ferrugineigula 20.05793
#> 4 Cinclodes_pabsti 30.27020
#> 5 Conopophaga_melanops 47.72685
#> 6 Herpsilochmus_pileatus 26.40947Com base na filogenia estudada, Tinamus solitarius (112,58 milhões de anos), Ortalis guttata (108,39 m.a.) e Aramides saracura (96,86 m.a.) são as espécies com maior distinção evolutiva devido a elevada fração dos ramos não compartilhado com as outras espécies.
13.3.2 Divergência da diversidade alfa filogenética
As métricas de divergência utilizam a média da distribuição das unidades extraídas da árvore filogenética (Tucker et al. 2017).
Mean Pairwise Distance (MPD)
Esta métrica utiliza a matriz de distância filogenética para quantificar a distância média do parentesco entre pares de espécies em uma comunidade. Este índice pode ser calculado considerando dados de incidência ou considerando dados de abundância das espécies. Importante, o MPD é uma métrica que pesa a estrutura interna da filogenia (e.g., relações entre espécies de famílias diferentes) (Webb et al. 2002).
Abaixo, demonstramos os códigos no R para o cálculo do MPD utilizando os dados das comunidades de aves.
Vamos iniciar com dados de incidência (presença e ausência) das espécies nas comunidades. A função cophenetic() gera uma matriz com as distâncias par a par entre as espécies. Essas distâncias são utilizadas para computar a distância média do parentesco das espécies dentro das comunidades.
## Mean Pairwise Distance (MPD)
# Análise com dados de incidência das espécies nas comunidades.
resultados_MPD_PA <- mpd(composicao_especies_P, cophenetic(filogenia_aves),
abundance.weighted = FALSE)
# Mostra os valores de MPD para cada comunidade.
resultados_MPD_PA
#> [1] 150.7914 157.3158 146.1622 154.5005 143.0727 141.1926 154.3145 141.4292 139.6198 143.0862A comunidade 9 abriga a composição de espécies mais aparentada (i.e. menor diversidade filogenética) com distância média entre as espécies de 139,62 milhões de anos. Por outro lado, a comunidade 2 abriga a composição de espécies menos aparentada (i.e. maior diversidade filogenética) com distância média de 157,31 milhões anos.
Vamos refazer a análise do MPD, mas desta vez, considerando a abundância das espécies de aves nas comunidades. Para isso, alteramos o argumento abundance.weighted = TRUE.
## Mean Pairwise Distance (MPD)
# Análise com dados de abundância das espécies nas comunidades.
resultados_MPD_AB <- mpd(composicao_especies_P, cophenetic(filogenia_aves),
abundance.weighted = TRUE)
# Mostra os valores de MPD para cada comunidade.
resultados_MPD_AB
#> [1] 135.0704 143.3156 129.1940 142.8127 131.4027 128.7733 134.0380 132.6389 133.4041 117.8787Percebam que pesando o comprimento do ramo pela abundância das espécies altera-se os valores do índice de diversidade filogenética. Neste caso, a comunidade 10 passa a ser a comunidade que abriga a composição de espécies mais aparentada (i.e. menor diversidade filogenética) com distância média entre as espécies de 117,88 milhões de anos.
Mean Nearest Taxon Distance (MNTD)
Esta métrica utiliza a matriz de distância filogenética para quantificar a média dos valores mínimos de parentesco entre pares de espécies em uma comunidade. Ou seja, qual o valor médio da distância para o vizinho mais próximo. Este índice pode ser calculado considerando dados de incidência (presença e ausência) ou considerando dados de abundância das espécies. Diferente do MPD, o MNTD é uma métrica terminal que pesa as relações nas pontas da filogenia (e.g. espécies dentro do mesmo gênero) (Webb et al. 2002).
Abaixo, demonstramos os códigos no R para o cálculo do MNTD utilizando os dados das comunidades de aves.
## Mean Nearest Taxon Distance (MNTD)
# Análise com dados de presença e ausência das espécies nas comunidades.
resultados_MNTD_PA <- mntd(composicao_especies_P, cophenetic(filogenia_aves),
abundance.weighted = FALSE)
# Mostra os valores de MPD para cada comunidade.
resultados_MNTD_PA
#> [1] 63.89727 66.15828 72.96912 67.67170 64.93477 63.72337 93.54980 78.24876 62.34565 112.23127A comunidade 9 abriga a composição de espécies com distância média do vizinho mais próximo de 62,34 milhões de anos. Esse resultado indica que as espécies terminais são mais aparentadas (e.g. espécies do mesmo gênero) do que a composição de espécies da comunidade 10 onde a distância média do vizinho mais próximo é 112,23 milhões de anos (e.g. espécies de gêneros diferentes).
Vamos refazer a análise do MNTD, mas desta vez, considerando a abundância das espécies de aves nas comunidades.
# Análise com dados de abundância das espécies nas comunidades.
resultados_MNTD_AB <- mntd(composicao_especies_P, cophenetic(filogenia_aves),
abundance.weighted = TRUE)
# Mostra os valores de MPD para cada comunidade.
resultados_MNTD_AB
#> [1] 57.11745 53.02212 70.47864 59.12049 61.23225 60.26180 110.13043 97.35404 82.12099 127.70084Como nos resultados do MPD, pesar o comprimento do ramo pela abundância das espécies altera os valores do MNTD. Neste caso, ao invés da comunidade 9, a comunidade 2 passa a ser a comunidade que abriga a composição de espécies com a menor distância média do vizinho mais próximo (53,02 milhões de anos).
📝 Importante
Perceba que ao determinar as análises com base na incidência ou abundância das espécies, você pode também alterar a interpretação dos padrões encontrados.
Phylogenetic Species Variability (PSV)
Esta métrica estima a quantidade relativa dos comprimentos dos ramos não compartilhados entre as comunidades. Quando todas as espécies em uma amostra não são aparentadas (i.e. filogenia em estrela), o valor do PSV é 1 (um), indicando máxima variabilidade. Quando as espécies tornam-se mais aparentadas, o valor de PSV aproxima-se de 0 (zero), indicando reduzida variabilidade. Os valores esperados de PSV são estatisticamente independentes da riqueza de espécies (Helmus et al. 2007).
📝 Importante
Os valores de PSV são idênticos ao MPD quando a filogenia é ultramétrica.
Abaixo, demonstramos os códigos no R para o cálculo do PSV utilizando os dados das comunidades de aves.
## Phylogenetic Species Variability (PSV)
# Análise com dados de presença e ausência das espécies nas comunidades.
resultados_PSV <- psv(composicao_especies_P,filogenia_aves)
# Mostra os valores de PSV para cada comunidade.
resultados_PSV
#> PSVs SR vars
#> Com_1 0.6697865 27 6.224834e-05
#> Com_2 0.6987378 26 7.221499e-05
#> Com_3 0.6492375 25 8.329332e-05
#> Com_4 0.6861589 25 8.329332e-05
#> Com_5 0.6355271 22 1.252245e-04
#> Com_6 0.6270572 18 2.140033e-04
#> Com_7 0.6853322 15 3.288296e-04
#> Com_8 0.6281778 12 5.361887e-04
#> Com_9 0.6200717 13 4.513324e-04
#> Com_10 0.6355626 9 9.812931e-04A comunidade 2 abriga a maior variabilidade filogenética (0,69) enquanto a comunidade 9 abriga a menor variabilidade (0,62). Perceba que os valores de PSV não são correlacionados com número de espécies nas comunidades (r = 0,59, p = 0,07).
13.3.3 Regularidade da diversidade alfa filogenética
As métricas de regularidade caracterizam a variação das distâncias entre as espécies em uma comunidade (Tucker et al. 2017).
Variance of Pairwise Distance (VPD)
Esta métrica utiliza a matriz de distância filogenética para quantificar a variância do parentesco entre pares de espécies em uma comunidade (Clarke and Warwick 2001).
Abaixo, demonstramos os códigos no R para o cálculo do VPD utilizando os dados das comunidades de aves.
## Variance of Pairwise Distance (VPD)
# Transformando data frame em matriz.
dados_matriz <- as.matrix(composicao_especies_P)
# Transformar os dados para o formato requerido pelo pacote pez.
dados <- comparative.comm(filogenia_aves, dados_matriz)
# Análise.
resultados_VPD <- .vpd(dados, cophenetic(filogenia_aves))
# Mostra os valores de VPD para cada comunidade.
resultados_VPD
#> Com_1 Com_10 Com_2 Com_3 Com_4 Com_5 Com_6 Com_7 Com_8 Com_9
#> 1619.4697 1031.8887 1828.1930 1630.4026 1317.9919 1465.1728 1519.6115 825.5349 1278.0076 1508.0495A comunidade 2 abriga a maior variância na distância filogenética entre pares de espécies dentro da comunidade (1828,19 milhões de anos) enquanto a comunidade 7 abriga a menor variância entre os pares de espécies (825,53 m.a.).
13.3.4 Correlação entre as métricas de diversidade alfa filogenética
Vamos avaliar a correlação entre os valores das métricas de diversidade alfa filogenética. Vamos criar um data frame com os resultados das métricas separados para as dimensões de riqueza e divergência. Não iremos fazer para regularidade, pois só apresentamos uma métrica de diversidade filogenética nesta dimensão (Figura 13.6).
## Data frame
# Vamos criar um data.frame com os resultados das métricas da dimensão riqueza.
metricas_riqueza <- data.frame(riqueza = resultados_PD$SR,
PD = resultados_PD$PD,
PSR = resultados_PSR$PSR,
PE = resultados_PE)
## Gráfico
# Gráfico mostrando na parte:
# i) inferior a distribuição dos pontos considerando as métricas pareadas
# ii) superior o valor da correlação de pearson
# iii) diagonal a curva de densidade
ggpairs(metricas_riqueza, upper = list(continuous = wrap("cor", size = 4))) +
tema_livro()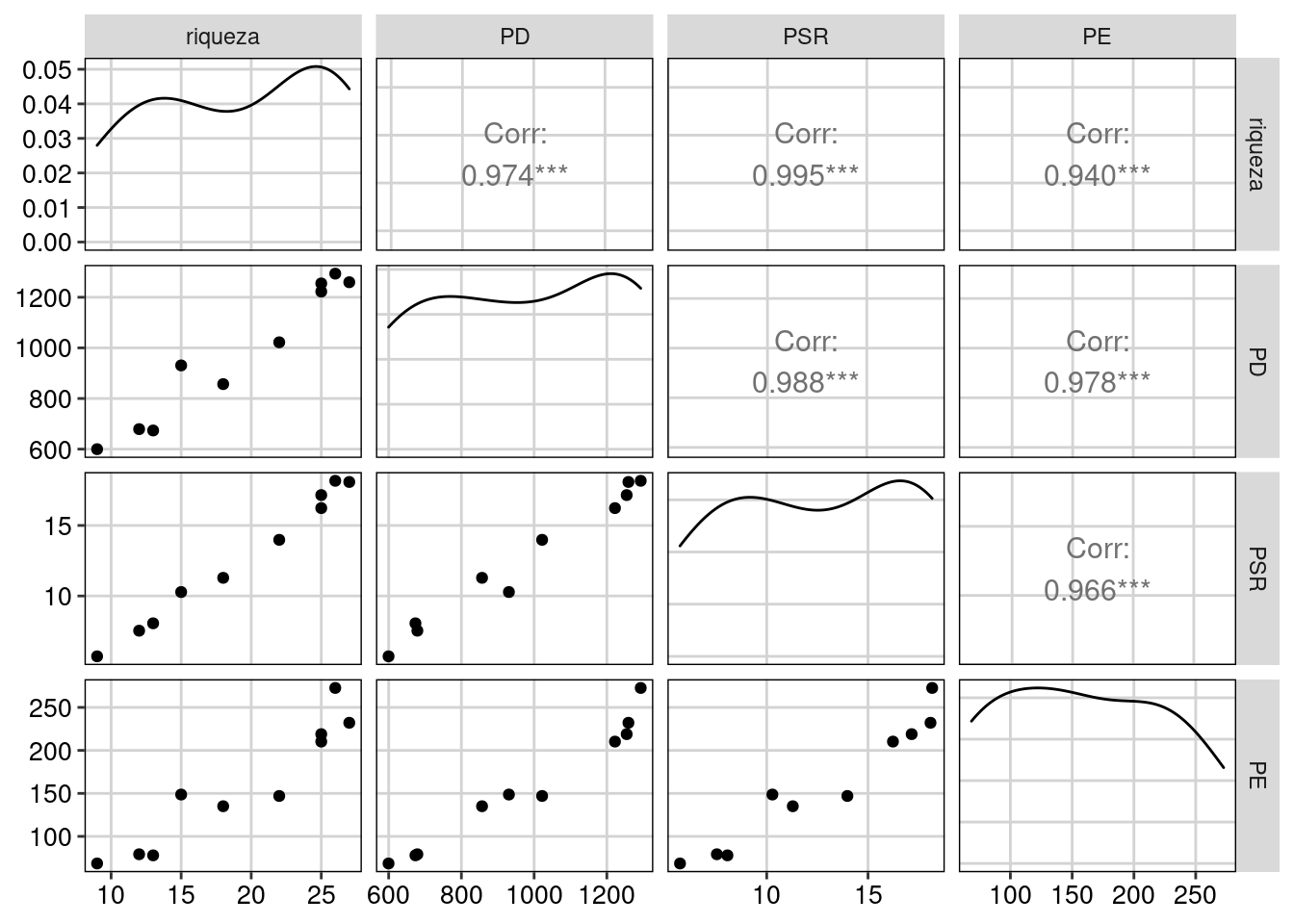
Figura 13.6: Correlação entre as métricas de riqueza da diversidade alfa filogenética.
Percebam que as três métricas apresentam correlações pareadas acima de 94%. Isso indica que as métricas são redundantes. Portanto, não há necessidade de calcular mais de uma métrica dentro da dimensão da riqueza filogenética. Além disso, as três métricas de diversidade alfa filogenética também apresentam alta correlação com a riqueza de espécies. Veja abaixo na seção de modelos nulos como controlar o efeito da riqueza de espécies nas métricas de diversidade filogenética.
Vamos avaliar a correlação entre os valores das métricas de diversidade alfa filogenética para a dimensão divergência (Figura 13.7).
## Data frame
# Vamos criar um data.frame com os resultados das métricas da dimensão divergência.
metricas_divergencia <- data.frame(riqueza = resultados_PD$SR,
MPD = resultados_MPD_PA,
MPD_AB = resultados_MPD_AB,
MNTD = resultados_MNTD_PA,
MNTD_AB = resultados_MNTD_AB,
PSV = resultados_PSV$PSVs)
## Gráfico
ggpairs(metricas_divergencia, upper = list(continuous = wrap("cor", size = 4))) +
tema_livro()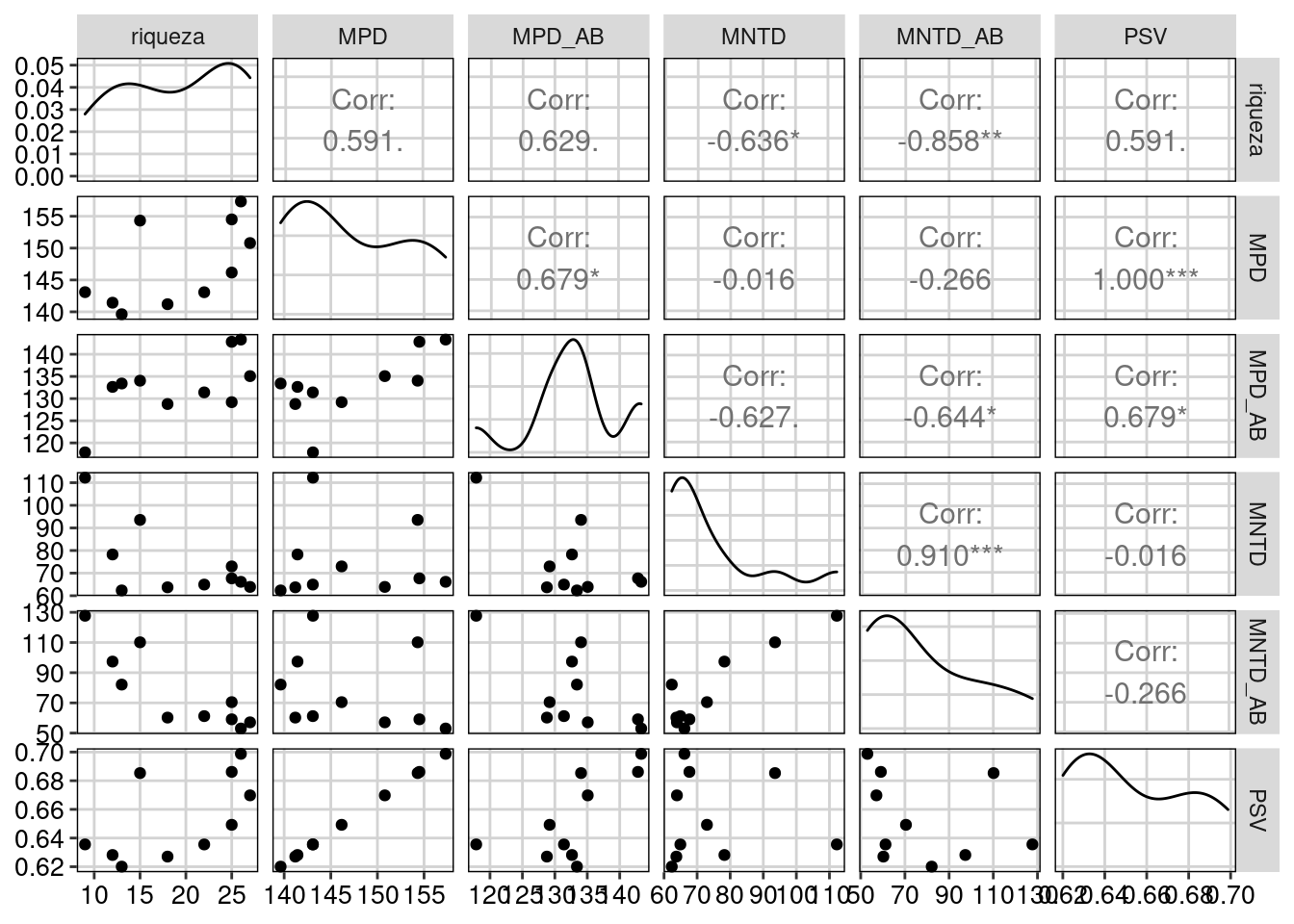
Figura 13.7: Correlação entre as métricas de divergência da diversidade alfa filogenética.
Como mencionado, as métricas MPD e PSV são idênticas quando usamos uma filogenia ultramétrica. Contudo, as métricas de divergência não apresentam correlações tão altas como as métricas da dimensão riqueza, com exceção do MNTD usando dados de incidência e abundância que foram fortemente correlacionados (r = 0,9). Além disso, estas métricas não são tão afetadas pela riqueza de espécies das comunidades como as métricas da dimensão riqueza.
13.3.5 Associação entre a diversidade alfa filogenética e o ambiente
Vamos avaliar e plotar a relação entre os valores de algumas métrica de diversidade alfa filogenética (variável resposta) e os valores de precipitação (variável preditora) (Figura 13.8).
## Dados
# Vamos inserir os dados de precipitação na planilha metrica_divergencia.
metricas_divergencia$precipitacao <- precipitacao_filogenetica$prec
## Gráficos
MPD_PA_plot <- ggplot(metricas_divergencia, aes(precipitacao, MPD)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
labs(x = "Precipitação (mm)",
y = "Mean Pairwise Distance\n (MPD - Ausência e Presença)") +
tema_livro()
MPD_AB_plot <- ggplot(metricas_divergencia, aes(precipitacao, MPD_AB)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
labs(x = "Precipitação (mm)",
y = "Mean Pairwise Distance\n (MPD - Abundância)", size = 8) +
tema_livro()
MNTD_AP_plot <- ggplot(metricas_divergencia, aes(precipitacao, MNTD)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
labs(x = "Precipitação (mm)",
y = "Mean Nearest Taxon Distance\n (MNTD - Ausência e Presença)",
size = 8) +
tema_livro()
MNTD_AB_plot <- ggplot(metricas_divergencia, aes(precipitacao, MNTD_AB)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
geom_smooth(method = lm, se = FALSE, color = "black") +
labs(x = "Precipitação (mm)",
y = "Mean Nearest Taxon Distance\n (MNTD - Abundância)",
size = 8) +
tema_livro()
ggarrange(MPD_PA_plot, MPD_AB_plot, MNTD_AP_plot, MNTD_AB_plot,
ncol = 2, nrow = 2)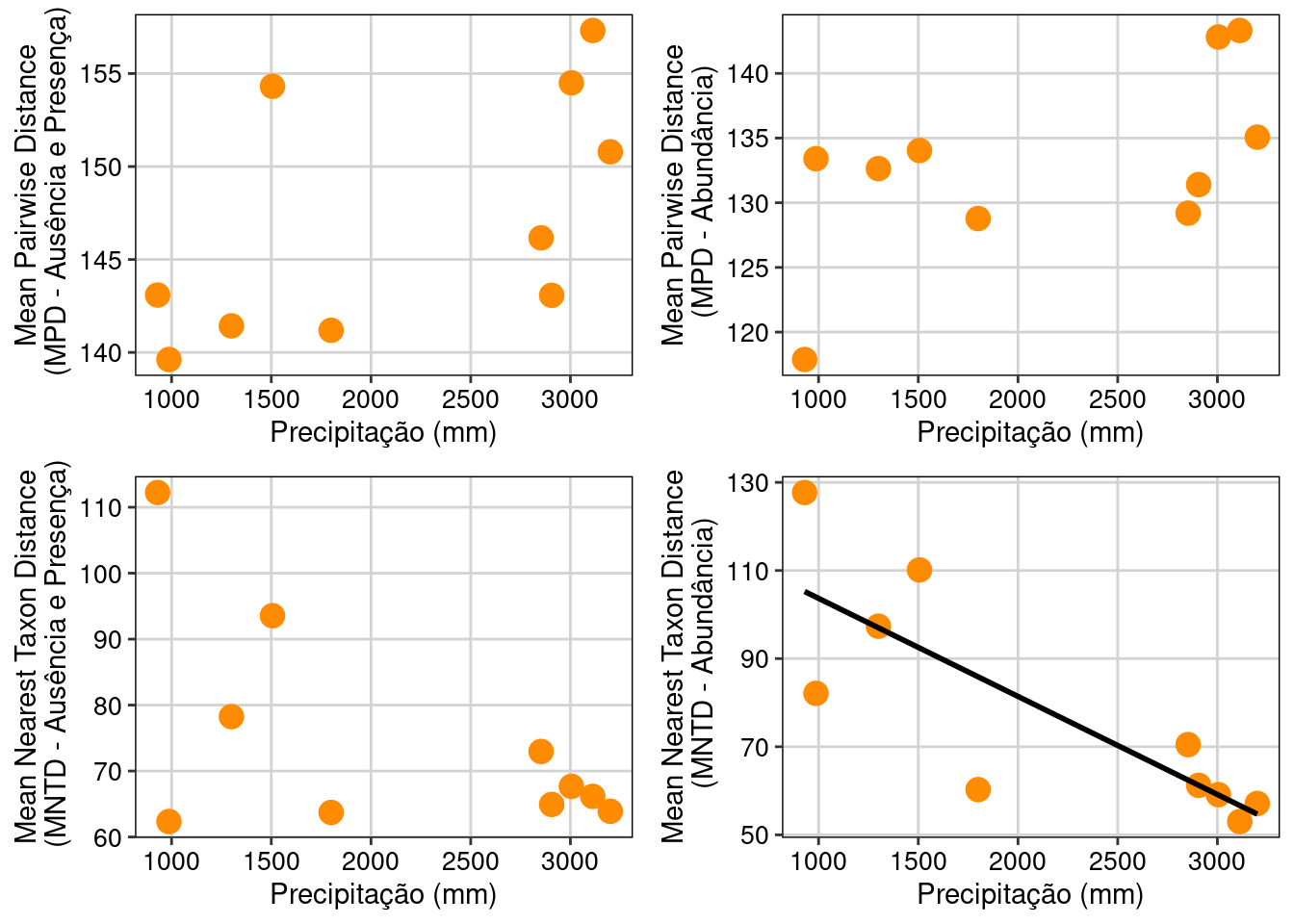
Figura 13.8: Relação de algumas métrica de diversidade alfa filogenética e valores de precipitação.
O MPD, que avalia as relações de parentesco mais internas da filogenia (i.e., relações entre espécies de famílias diferentes) não apresentou associação com o gradiente de precipitação. Por outro lado, o MNTD que avalia as relações mais terminais da filogenia (i.e., espécies dentro do mesmo gênero) apresentou uma relação negativa com o gradiente de precipitação. Interessante que a associação só foi significativa quando pesamos a análise pela abundância das espécies nas comunidades. Esses resultados demonstram a importância da seleção das métricas de diversidade filogenética e tipos de dados (e.g., incidência ou abundância) utilizados na interpretação dos padrões observados na natureza.
Vamos ver os gráficos das métricas da dimensão riqueza da diversidade alfa filogenética (Figura 13.9).
## Dados
# Vamos inserir os dados de precipitação na planilha metrica_riqueza.
metricas_riqueza$precipitacao <- precipitacao$prec
## Gráficos
Riqueza_plot <- ggplot(metricas_riqueza, aes(precipitacao, riqueza)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
geom_smooth(method = lm, se = FALSE, color = "black") +
labs(x = "Precipitação (mm)", y = "Riqueza de espécies") +
tema_livro()
PD_plot <- ggplot(metricas_riqueza, aes(precipitacao, PD)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
geom_smooth(method = lm, se = FALSE, color = "black") +
labs(x = "Precipitação (mm)",
y = "Diversidade Filogenética\n (Faith)", size = 8) +
tema_livro()
PSR_plot <- ggplot(metricas_riqueza, aes(precipitacao, PSR)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
geom_smooth(method = lm, se = FALSE, color = "black") +
labs(x = "Precipitação (mm)",
y = "Phylogenetic Species Richness\n (PSR)",
size = 8) +
tema_livro()
PE_plot <- ggplot(metricas_riqueza, aes(precipitacao, PE)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
geom_smooth(method = lm, se = FALSE, color = "black") +
labs(x = "Precipitação (mm)",
y = "Phylogenetic Endemism\n (PE)",
size = 8) +
tema_livro()
ggarrange(Riqueza_plot, PD_plot, PSR_plot, PE_plot, ncol = 2, nrow = 2)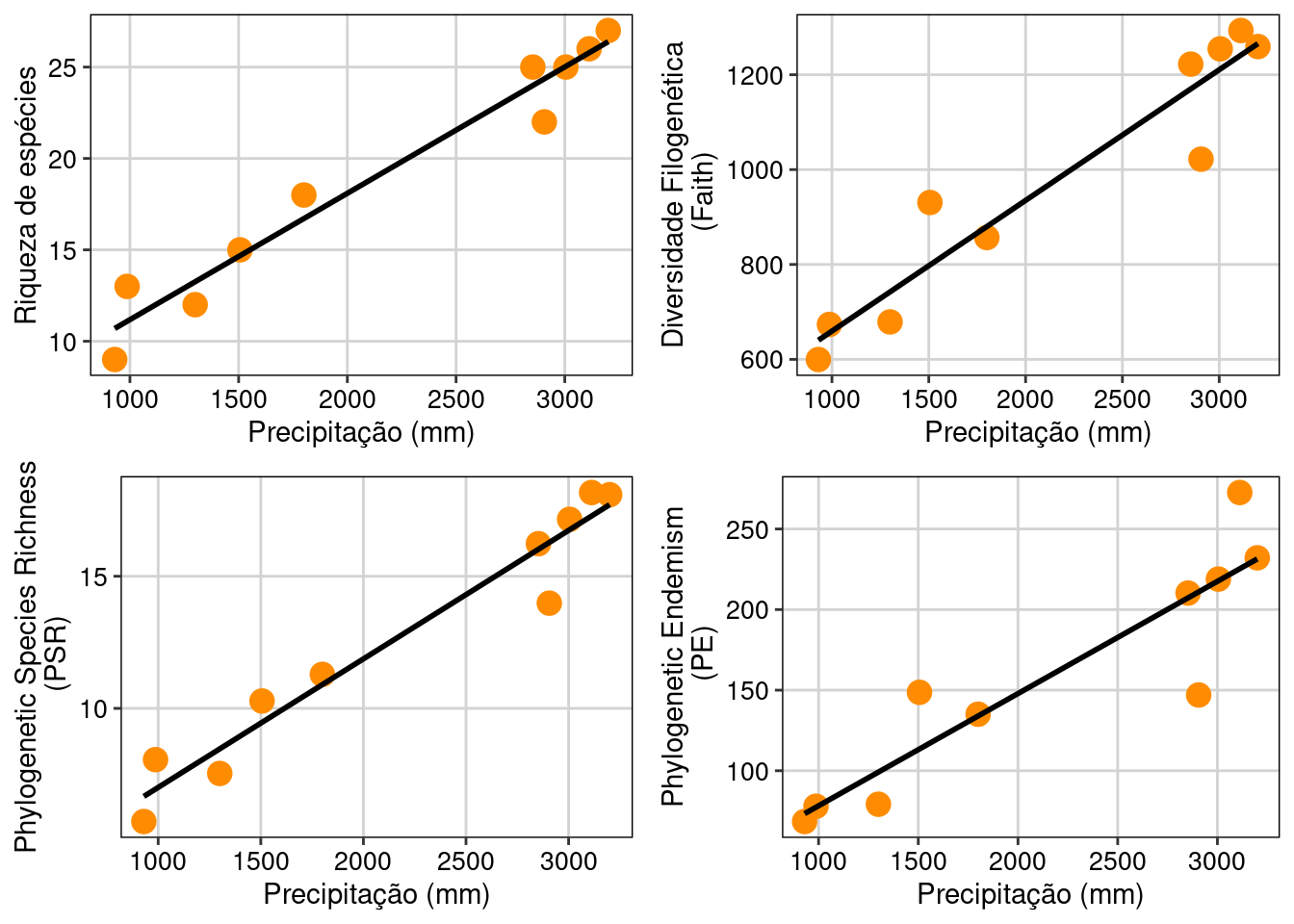
Figura 13.9: Relação de algumas métrica de diversidade alfa filogenética e valores de precipitação.
As três métricas de diversidade filogenética foram relacionadas com o gradiente de precipitação. Esse resultado indica que comunidades localizadas em áreas com maior precipitação anual abrigaram maior diversidade filogenética do que comunidades localizadas em áreas mais secas. Contudo, estas métricas são dependentes da riqueza de espécies nas comunidades. Veja abaixo a seção de modelos nulos para entender como lidar com essa dependência.
13.4 Métricas de diversidade beta filogenética
Métricas de diversidade beta filogenética utilizam dados de presença e ausência ou abundância das espécies para determinar um valor que representa a diferença entre comunidades em relação a história evolutiva das linhagens (para detalhes de diversidade beta, consulte o Capítulo 12).
13.4.1 Divergência da diversidade beta filogenética
Community Mean Pairwise Distance (COMDIST)
Esta métrica é uma extensão do MPD. COMDIST calcula a média da distância filogenética entre as espécies de duas comunidades (Webb, Ackerly, and Kembel 2008). COMDIST pode ser calculada usando dados de incidência (presença e ausência) ou abundância das espécies. Esta extensão do MPD também é conhecida na literatura como Dpw (Swenson 2011, 2014).
Abaixo, demonstramos os códigos no R para o cálculo do COMDIST utilizando os dados das comunidades de aves.
## Community Mean Pairwise Distance (COMDIST)
# Análise com dados de presença e ausência das espécies nas comunidades.
resultados_Comdist_PA <- comdist(composicao_especies_P,
cophenetic(filogenia_aves),
abundance.weighted = FALSE)
resultados_Comdist_PA
#> Com_1 Com_2 Com_3 Com_4 Com_5 Com_6 Com_7 Com_8 Com_9
#> Com_2 150.5242
#> Com_3 144.3300 148.7436
#> Com_4 149.4782 153.2992 147.5838
#> Com_5 141.8435 146.9829 139.9606 145.8746
#> Com_6 142.6019 148.3160 140.0376 143.1340 137.9527
#> Com_7 147.7189 150.2248 147.1703 150.3418 144.1481 145.2975
#> Com_8 141.3083 145.6684 138.5875 145.3897 137.0034 137.7062 144.4818
#> Com_9 141.6018 146.4697 138.3515 144.3480 136.9036 136.3453 144.3257 130.7628
#> Com_10 140.8810 145.9333 136.9978 145.1400 136.5394 137.2350 144.3660 130.0691 130.2321As comunidades 8 e 10 apresentaram a menor média na distância filogenética (130,06 m.a. - espécies de linhagens mais próximas) entre as espécies presente em cada comunidade, enquanto as comunidades 2 e 4 apresentaram a maior média na distância filogenética (153.29 m.a. - espécies de linhagens mais distintas).
Vamos refazer a análise do COMDIST, mas desta vez, considerando a abundância das espécies de aves nas comunidades.
## Community Mean Pairwise Distance (COMDIST)
# Análise com dados de abundância das espécies nas comunidades.
resultados_Comdist_AB <- comdist(composicao_especies_P,
cophenetic(filogenia_aves),
abundance.weighted = TRUE)Como no caso do MPD, pensar a abundância das espécies altera o padrão de distribuição dos valores de COMDIST. Neste caso, ao invés das comunidades 2 e 4, as comunidades 2 e 10 apresentam a maior média na distância filogenética (155,85 m.a.).
Community Mean Nearest Taxon Distance (COMDISTNT)
Esta métrica é uma extensão do MNTD. COMDISTNT calcula a média da distância filogenética entre o táxon mais próximo das espécies de duas comunidades (Webb, Ackerly, and Kembel 2008). COMDISTNT pode ser calculada usando dados de incidência ou abundância das espécies. Esta extensão do MNTD também é conhecida na literatura como Dnn (Swenson 2011).
Abaixo, demonstramos os códigos no R para o cálculo do COMDISTNT utilizando os dados das comunidades de aves.
## Community Mean Nearest Taxon Distance (COMDISTNT)
# Análise com dados de presença e ausência das espécies nas comunidades.
resultados_Comdistnt_PA <- comdistnt(composicao_especies_P,
cophenetic(filogenia_aves),
abundance.weighted = FALSE)
resultados_Comdistnt_PA
#> Com_1 Com_2 Com_3 Com_4 Com_5 Com_6 Com_7 Com_8 Com_9
#> Com_2 24.65946
#> Com_3 18.56953 22.22310
#> Com_4 26.85806 24.04505 17.87073
#> Com_5 13.15074 34.14223 18.82684 25.54000
#> Com_6 35.43332 49.33726 33.82511 24.59980 28.50505
#> Com_7 30.37968 29.22411 39.89649 34.06858 29.27588 47.69536
#> Com_8 38.16628 48.17376 38.46830 51.02029 32.52846 50.37593 54.37647
#> Com_9 42.58727 54.09441 41.83792 46.29635 36.35245 46.18264 49.85495 10.69759
#> Com_10 45.71452 56.82713 40.39642 60.17935 40.74857 59.63770 60.24556 10.87162 16.12367As comunidades 8 e 9 apresentaram a menor média na distância do vizinho mais próximo (10,69 m.a. - espécies do mesmo gênero ou gêneros irmãos) entre as espécies presente em cada comunidade, enquanto as comunidades 7 e 10 apresentaram a maior média na distância entre vizinhos (60,24 m.a. - espécies de linhagens distintas).
Vamos refazer a análise do COMDISTNT, mas desta vez, considerando a abundância das espécies de aves nas comunidades.
## Community Mean Nearest Taxon Distance (COMDISTNT)
# Análise com dados de abundância das espécies nas comunidades.
resultados_Comdistnt_AB <- comdistnt(composicao_especies_P,
cophenetic(filogenia_aves),
abundance.weighted = TRUE)As comunidades 8 e 10 apresentaram a menor média na distância do vizinho mais próximo (5,64 m.a.) entre as espécies presente em cada comunidade, enquanto as comunidades 6 e 10 apresentaram a maior média na distância entre vizinhos (82,62 m.a.).
13.4.2 Correlação entre as métricas de diversidade beta filogenética
Vamos avaliar a correlação entre os valores das métricas da diversidade beta filogenética para a dimensão divergência (Figura 13.10).
## Dados
# Vamos criar um data frame com os resultados das métricas da dimensão divergência.
metricas_divergencia_beta <- data.frame(
COMDIST_PA = as.numeric(resultados_Comdist_PA),
COMDIST_AB = as.numeric(resultados_Comdist_AB),
COMDISTNT_PA = as.numeric(resultados_Comdistnt_PA),
COMDISTNT_AB = as.numeric(resultados_Comdistnt_AB))
## Gráfico
ggpairs(metricas_divergencia_beta,
upper = list(continuous = wrap("cor", size = 4))) +
tema_livro()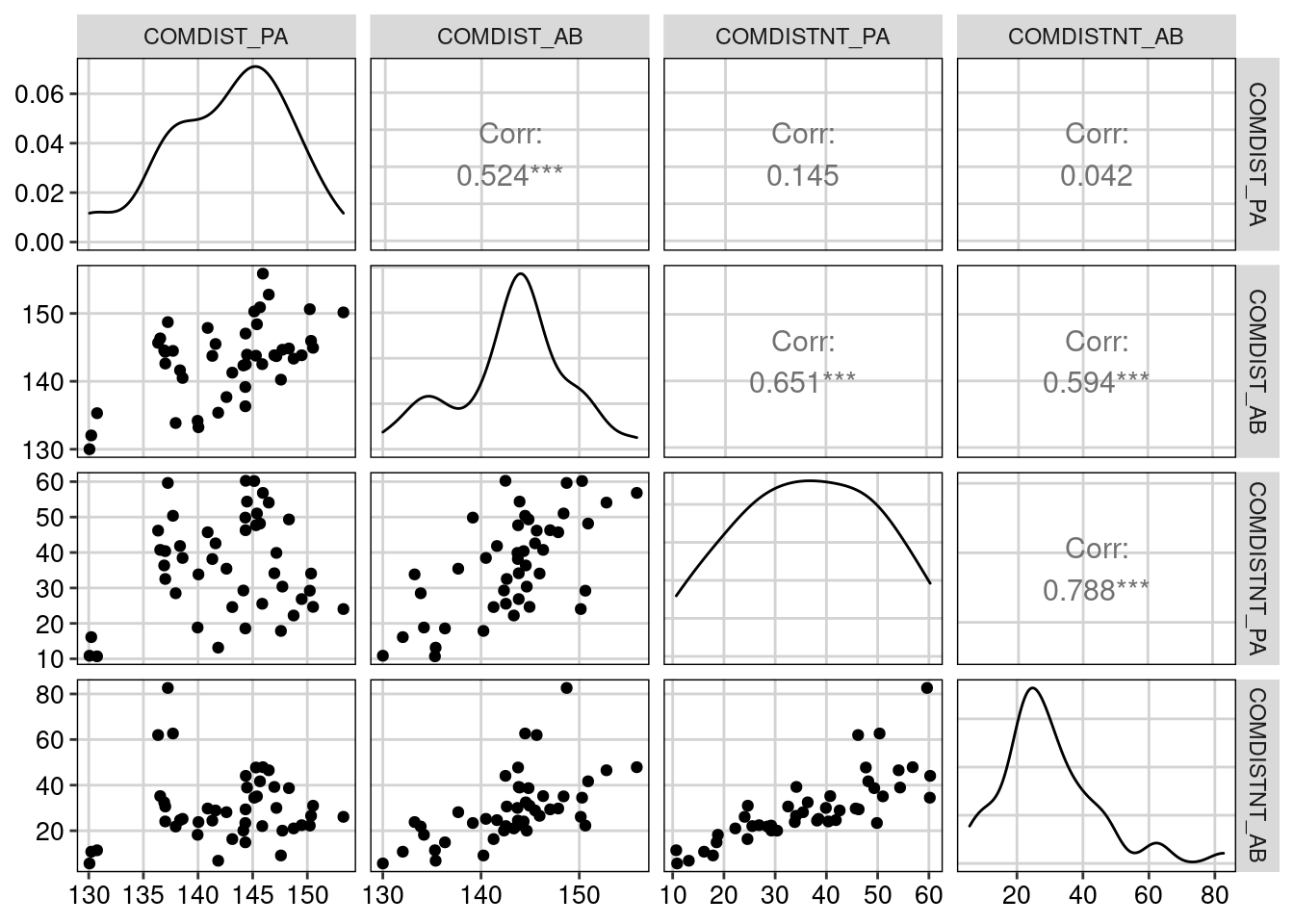
Figura 13.10: Correlação entre as métricas de divergência da diversidade beta filogenética.
Os valores das métricas de divergência filogenética beta apresentam correlações mais baixas do que as métricas da dimensão riqueza. Lembrem-se que COMDIST e COMDISTNT dão pesos diferentes para as relações de parentesco. COMDIST pesa as relações mais basais e internas da filogenia, enquanto COMDISTNT pesa as relações nas partes terminais da filogenia. Portanto, elas podem trazer informações complementares.
13.4.3 Associação entre a divergência da diversidade beta filogenética e o ambiente
Vamos avaliar e plotar a relação entre os valores de algumas métricas de divergência da diversidade beta filogenética (variável resposta) e os valores de precipitação (variável preditora) (Figura 13.11).
## Dados
# Precisamos calcular a dissimilaridade par a par da precipitação entre as comunidades.
dis_prec <- vegdist(precipitacao, "euclidian")
# Vamos inserir estes dados na planilha metrica_divergencia_beta.
metricas_divergencia_beta$dis_prec <- as.numeric(dis_prec)
# Gráficos.
COMDIST_PA_plot <- ggplot(metricas_divergencia_beta,
aes(dis_prec, COMDIST_PA)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
labs(x = "Diferença na precipitação (mm)",
y = "COMDIST\n (Presença e Ausência)") +
tema_livro()
COMDIST_AB_plot <- ggplot(metricas_divergencia_beta,
aes(dis_prec, COMDIST_AB)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
geom_smooth(method = lm, se = FALSE, color = "black") +
labs(x = "Diferença na precipitação (mm)",
y = "COMDIST\n (Abundância)", size = 8) +
tema_livro()
COMDISTNT_PA_plot <- ggplot(metricas_divergencia_beta,
aes(dis_prec, COMDISTNT_PA)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
geom_smooth(method = lm, se = FALSE, color = "black") +
labs(x = "Diferença na precipitação (mm)",
y = "COMDISTNT\n (Ausência e Presença)",
size = 8) +
tema_livro()
COMDISTNT_AB_plot <- ggplot(metricas_divergencia_beta,
aes(dis_prec, COMDISTNT_AB)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
labs(x = "Diferença na precipitação (mm)",
y = " COMDISTNT\n (Abundância)",
size = 8) +
tema_livro()
ggarrange(COMDIST_PA_plot, COMDIST_AB_plot, COMDISTNT_PA_plot,
COMDISTNT_AB_plot, ncol = 2, nrow = 2)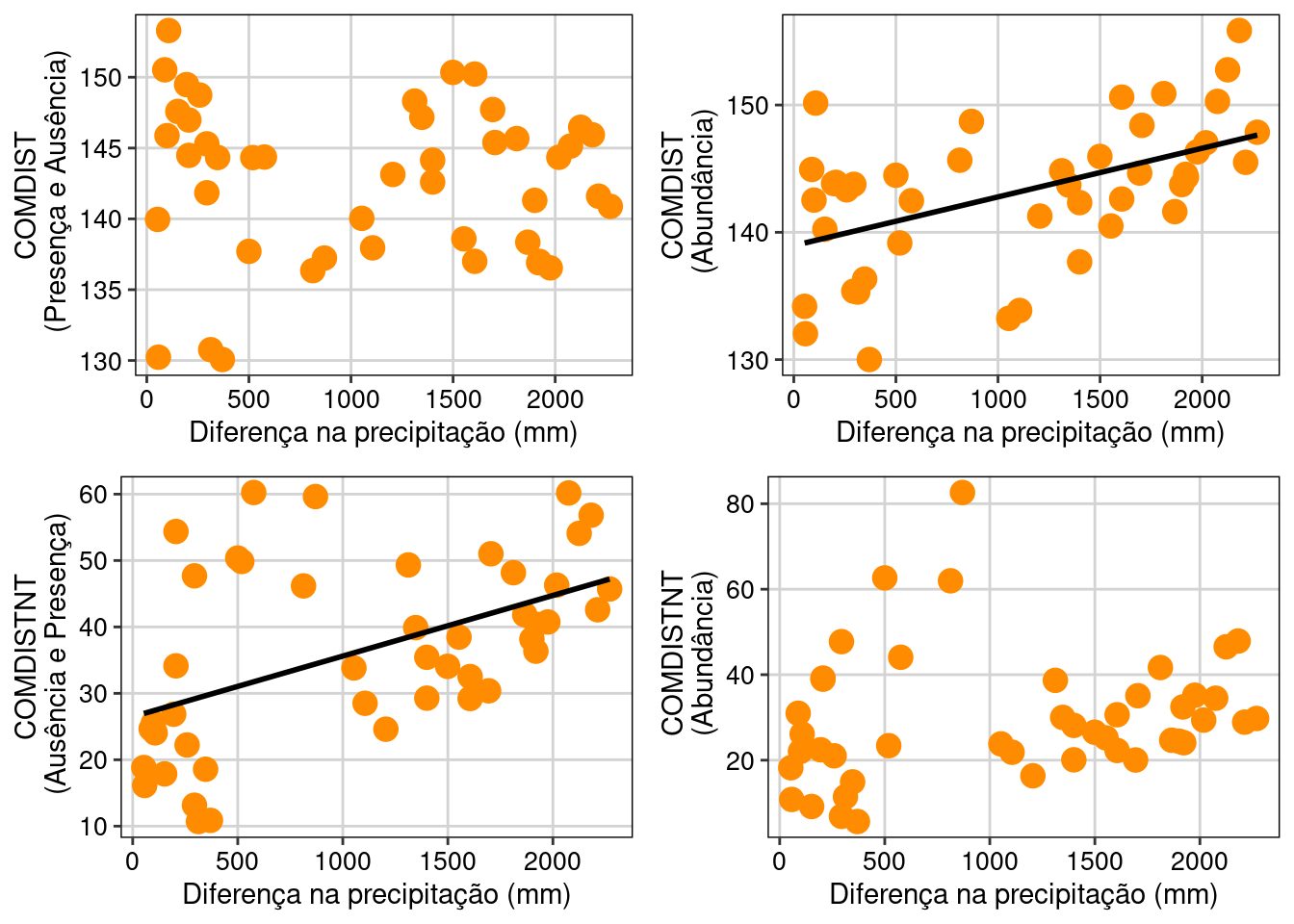
Figura 13.11: Relação de algumas métrica de divergência diversidade beta filogenética e valores de precipitação.
O COMDIST que avalia as relações de parentesco mais internas da filogenia (i.e., relações entre espécies de famílias diferentes) apresentou associação com o gradiente de precipitação quando avaliado pesado pela abundância das espécies. Por outro lado, o COMDISTNT que avalia as relações mais terminais da filogenia (i.e., espécies dentro do mesmo gênero) apresentou uma relação negativa com o gradiente de precipitação quando avaliado usando a incidência das espécies.
13.4.4 Riqueza da diversidade beta filogenética
Phylogenetic index of beta diversity (Phylosor)
Phylosor é uma métrica de similaridade e determina o comprimento total dos ramos da filogenia que é compartilhado entre pares de comunidades (Bryant et al. 2008).
Abaixo, demonstramos os códigos no R para o cálculo do Phylosor utilizando os dados das comunidades de aves.
## Phylogenetic index of beta diversity (Phylosor)
# Análise com dados de presença e ausência das espécies nas comunidades.
resultados_Phylosor <- phylosor(composicao_especies_P, filogenia_aves)
# Mostra uma matriz triangular com a similaridade entre a fração dos ramos
# compartilahdos entre duas comunidades
resultados_Phylosor
#> Com_1 Com_2 Com_3 Com_4 Com_5 Com_6 Com_7 Com_8 Com_9
#> Com_2 0.7856828
#> Com_3 0.8052839 0.7794964
#> Com_4 0.7831520 0.8066793 0.8595462
#> Com_5 0.8586780 0.6919478 0.8083230 0.7930266
#> Com_6 0.6717414 0.5827551 0.6977734 0.7494945 0.7383098
#> Com_7 0.7414284 0.7325727 0.6836231 0.7289449 0.7384561 0.6425717
#> Com_8 0.6826177 0.6283918 0.6443193 0.6404373 0.7123197 0.5928097 0.6146854
#> Com_9 0.6789983 0.6074676 0.6405220 0.6727656 0.7082867 0.6169977 0.6506880 0.9016007
#> Com_10 0.6264594 0.5709671 0.6422800 0.5823317 0.6493935 0.5362575 0.6015983 0.9106658 0.8607104As espécies presentes nas comunidades 6 e 10 compartilham a menor porção do comprimento dos ramos da filogenia (53% - menor similaridade entre os pares de comunidades), enquanto as espécies presentes nas comunidades 8 e 10 compartilham grande parte dos comprimentos dos ramos da filogenia (91% - maior similaridade entre os pares de comunidades).
Unique Fraction metric (UniFrac)
UniFrac é uma métrica de dissimilaridade e determina a fração única da filogenia contida em cada uma das duas comunidades (Lozupone and Knight 2005).
Abaixo, demonstramos os códigos no R para o cálculo da UniFrac utilizando os dados das comunidades de aves.
## Unique Fraction metric (UniFrac)
# Análise com dados de presença e ausência das espécies nas comunidades.
resultados_UniFrac <- unifrac(composicao_especies_P, filogenia_aves)As espécies presentes nas comunidades 6 e 10 apresentam a menor dissimilaridade (16,4 % - maior fração única da filogenia em cada comunidade), enquanto as espécies presentes nas comunidades 8 e 10 apresentam a maior dissimilaridade (63,36 % - maior compartilhamento de ramos da filogenia entre os pares de comunidades).
13.4.5 Correlação entre Phylosor e Unifrac
Vamos calcula a correlação entre as duas métricas de Riqueza da diversidade beta filogenética: Phylosor e Unifrac (Figura 13.12).
## Dados
# Vamos criar um data.frame com os resultados das métricas separados
# para as dimensões de riqueza e divergência.
metricas_riqueza_beta <- data.frame(Phylosor = as.numeric(resultados_Phylosor),
UniFrac = as.numeric(resultados_UniFrac))
## Gráfico
ggpairs(metricas_riqueza_beta, upper=list(continuous = wrap("cor", size = 4))) +
tema_livro()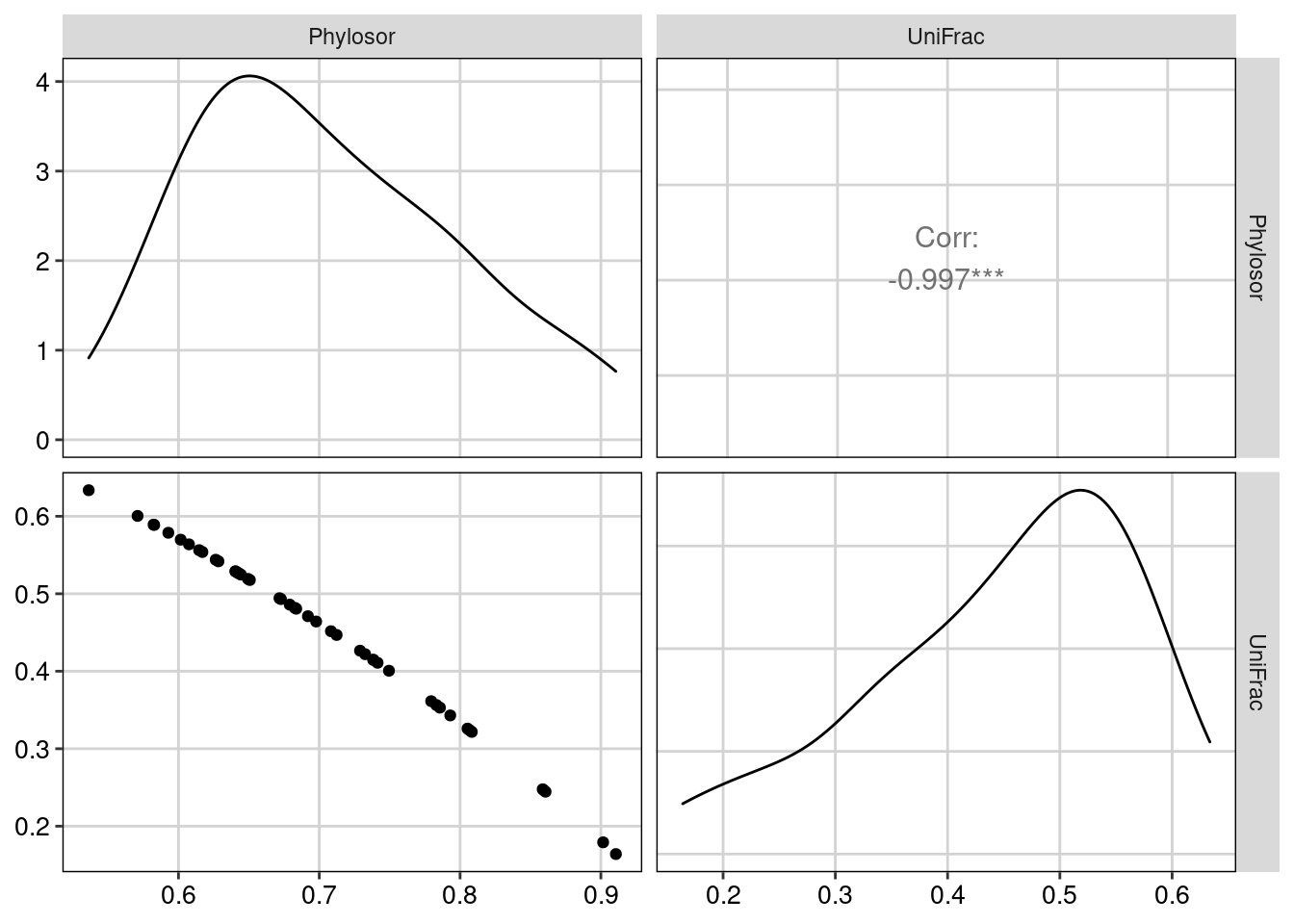
Figura 13.12: Correlação entre as métricas de riqueza da diversidade beta filogenética.
📝 Importante
Os valores de Phylosor e UniFrac apresenta 99% de correlação entre eles. Portanto, essas duas métricas identificam padrões idênticos e não devem ser utilizadas simultaneamente.
13.4.6 Associação entre a riqueza da diversidade beta filogenética e o ambiente
Vamos avaliar e plotar a relação entre os valores de algumas métricas de riqueza da diversidade beta filogenética (variável resposta) e os valores de precipitação (variável preditora) (Figura 13.13).
## Dados
# Vamos inserir os dados de precipitação na planilha metrica_riqueza_beta.
metricas_riqueza_beta$dis_prec <- as.numeric(dis_prec)
## Gráficos
# Phylosor.
plot_phylosor <- ggplot(metricas_riqueza_beta, aes(dis_prec, Phylosor)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
geom_smooth(method = lm, se = FALSE, color = "black") +
scale_y_continuous(limits = c(0, 1.0)) +
labs(x = "Diferença na precipitação (mm)",
y = "Phylosor", size = 8) +
tema_livro()
# Unifrag.
plot_unifrac <- ggplot(metricas_riqueza_beta, aes(dis_prec, UniFrac)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
geom_smooth(method = lm, se = FALSE, color = "black") +
scale_y_continuous(limits = c(0, 1.0)) +
labs(x = "Diferença na precipitação (mm)",
y = "UniFrac", size = 8) +
tema_livro()
ggarrange(plot_phylosor, plot_unifrac, ncol = 2)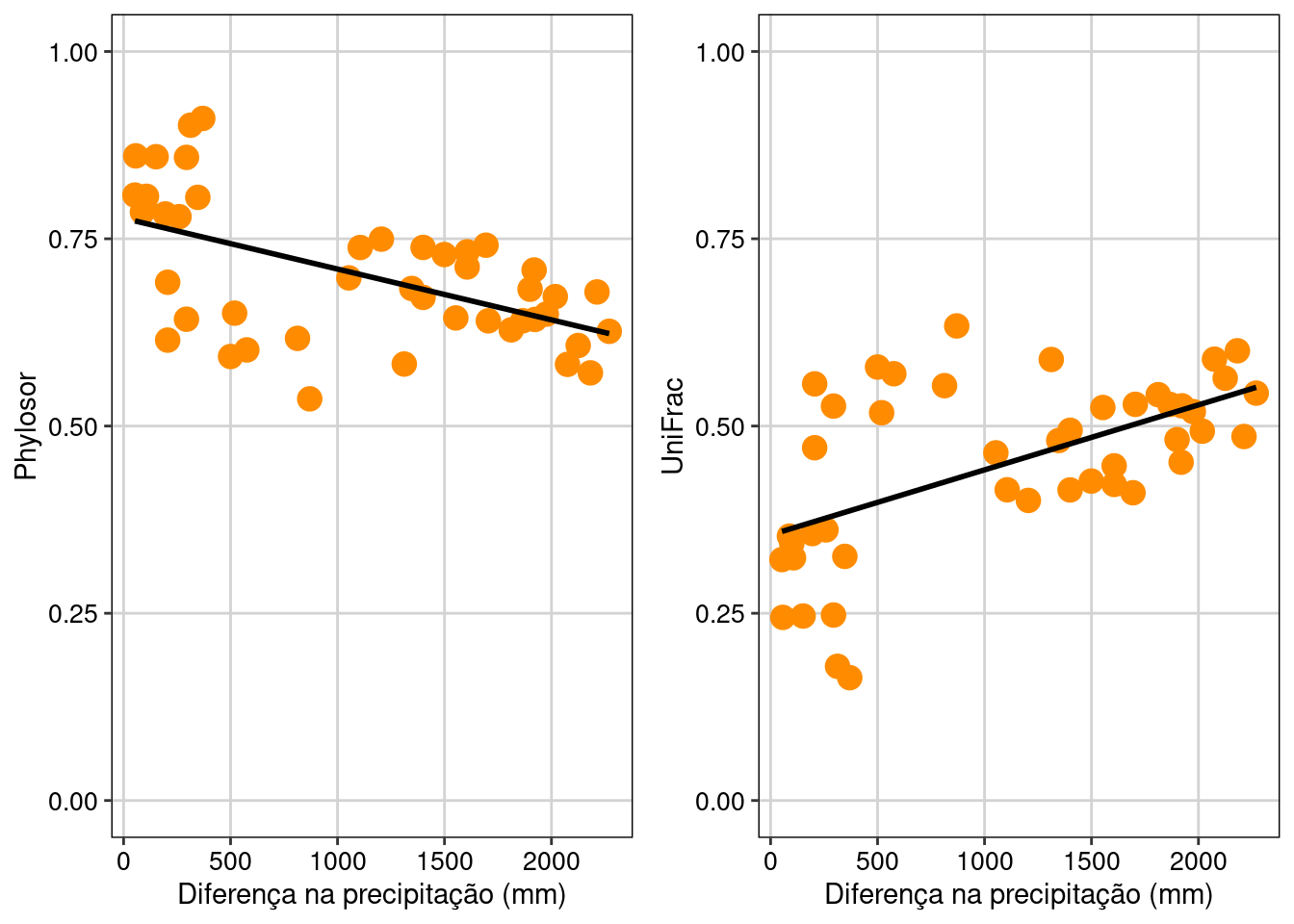
Figura 13.13: Relação de algumas métrica de riqeuza diversidade beta filogenética e valores de precipitação.
Phylosor (similaridade) e UniFrac (dissimilaridade) foram relacionadas com o gradiente de precipitação. Comunidades com quantidade de precipitação parecidas abrigaram linhagens similares enquanto comunidades que recebem quantidade de precipitação diferentes abrigam linhagens mais distintas.
13.4.7 Partição da diversidade beta filogenética
As métricas, Phylosor e UniFrac, podem ser particionadas em dois componentes (Baselga 2010; Leprieur et al. 2012): i) substituição (do inglês turnover) de espécies entre as comunidades; e ii) componente de aninhamento (do inglês nestedness) que representa a perda ou ganho de espécies entre comunidades atribuídos a diferença na riqueza de espécies. A partição da diversidade beta nestes componentes permite avaliar diferentes hipóteses sobre os processos e mecanismos atuando na montagem de comunidades.
Abaixo, demonstramos os códigos no R para o cálculo da partição da diversidade beta filogenética utilizando os dados das comunidades de aves.
## Partição
# Temos que transformar os dados para presença e ausência das espécies nas comunidades.
dados_PA <- decostand(composicao_especies_P, "pa")
# Partição dos componentes do Phylosor.
resultados_Phylosor_particao <- phylo.beta.pair(dados_PA,
filogenia_aves,
index.family = "sorensen")Vamos refazer a análise para UniFrac.
# Partição dos componentes do UniFrac.
resultados_UniFrac_particao <- phylo.beta.pair(dados_PA,
filogenia_aves,
index.family = "jaccard")
# Resultado tem três matrizes:
# i) dissimilaridade total (phylo.beta.jac);
# ii) componente substituição de espécies (phylo.beta.jtu); e
# iii) componente aninhamento (phylo.beta.jne).
# resultados_UniFrac_particao (para ver os resultados corra este comando)Gráfico com os resultados dos componentes substituição e aninhamento da diversidade beta filogenética - Phylosor (Figura 13.14).
## Dados
# Vamos preparar os dados para o gráfico.
particao_phylosor <- data.frame(
substituicao = as.numeric(resultados_Phylosor_particao$phylo.beta.sim),
aninhamento = as.numeric(resultados_Phylosor_particao$phylo.beta.sne),
sorensen = as.numeric(resultados_Phylosor_particao$phylo.beta.sor),
dis_prec = as.numeric(dis_prec))
## Gráficos
sorensen_plot <- ggplot(particao_phylosor,
aes(dis_prec, sorensen)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
geom_smooth(method = lm, se = FALSE, color = "black") +
labs(x = "", y = "Sorensen") +
tema_livro()
subst_plot <- ggplot(particao_phylosor,
aes(dis_prec, substituicao)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
geom_smooth(method = lm, se = FALSE, color = "black") +
labs(x = "Diferença na precipitação\n (mm)",
y = "Componente Substituição", size = 8) +
tema_livro()
aninha_plot <- ggplot(particao_phylosor,
aes(dis_prec, aninhamento)) +
geom_point(size = 4, shape = 19, col = "darkorange") +
geom_smooth(method = lm, se = FALSE, color = "black") +
labs(x = "", y = "Componente aninhamento", size = 8) +
tema_livro()
ggarrange(sorensen_plot, subst_plot, aninha_plot,
ncol = 3, nrow = 1)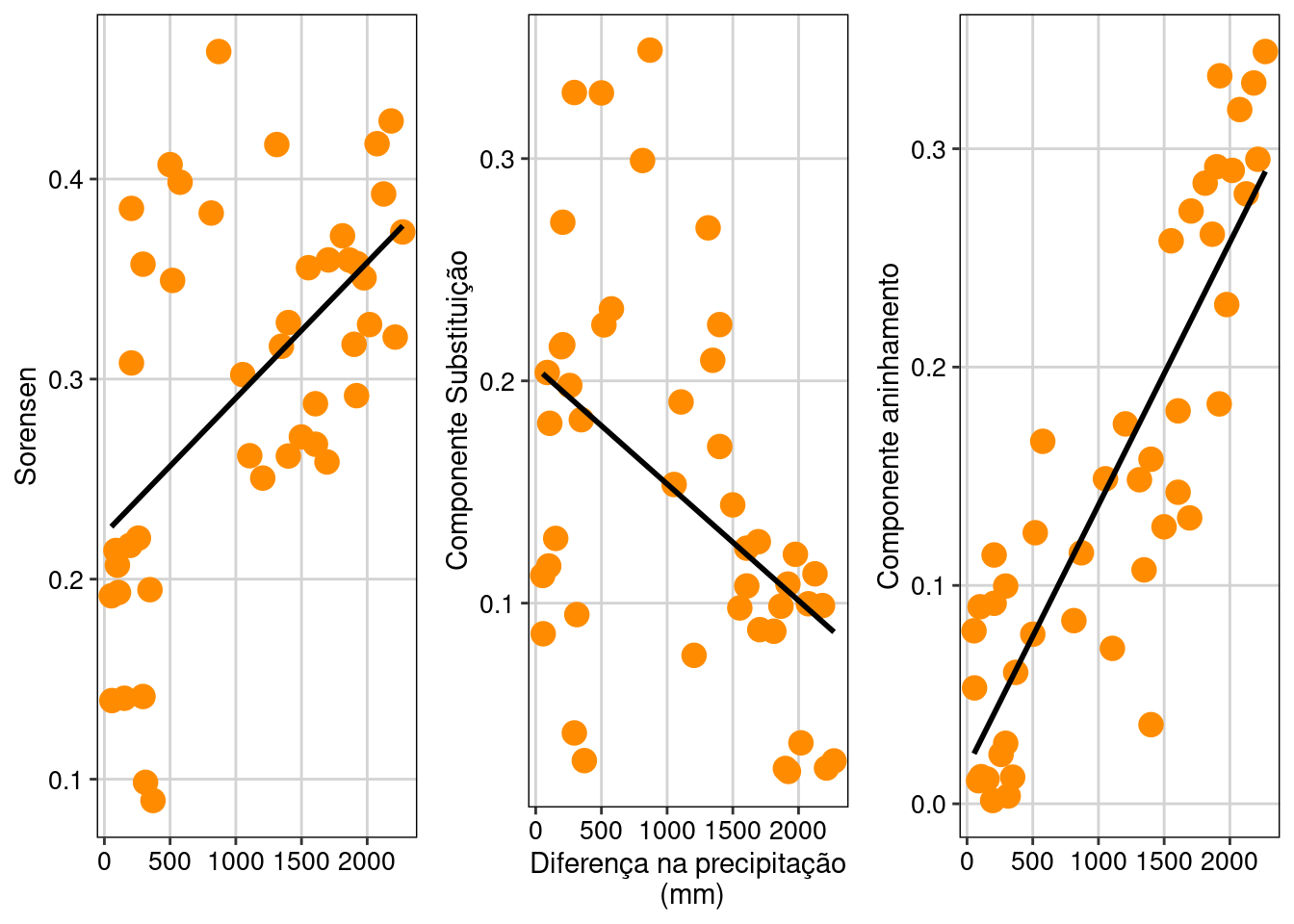
Figura 13.14: Relação dos componentes substituição e aninhamento da diversidade beta filogenética - Phylosor e valores de precipitação.
Percebam que o componente substituição é maior entre comunidades que apresentam diferenças altas na quantidade de precipitação, enquanto o componente aninhamento é maior entre as comunidades que apresentam quantidade similar de precipitação.
13.5 Modelos Nulos
Em muitos casos, os valores de diversidade filogenética são correlacionados com a riqueza de espécies nas comunidades. Por exemplo, se um pesquisador relata que duas comunidades apresentam diferentes valores de PD, é impossível saber se esta diferença é simplesmente porque elas têm diferentes valores de riqueza de espécies ou se há algum fator fundamental sobre a informação filogenética que é importante. Outra questão abordada nos estudos de montagem das comunidades é saber se os valores observados para as métricas (e.g. MPD ou MNTD) relacionadas com a estrutura filogenética das comunidades seriam diferentes se a colonização das espécies do pool regional fosse aleatória? Os modelos nulos respondem a estas perguntas. Contudo, a definição do pool regional não é uma tarefa trivial (Lessard et al. 2012; Carstensen et al. 2013).
Os modelos nulos são construídos considerando processos ecológicos ou evolutivos de interesse. Eles geram padrões que são baseados na aleatorização dos dados ecológicos ou amostragens aleatórias de uma distribuição conhecida ou hipotética (Gotelli and Graves 1996). Neste caso, alguns elementos dos dados (como colunas ou linhas) são mantidos constantes, e outros são permitidos variar aleatoriamente para criar novos padrões. O principal motivo para a construção de modelos nulos é produzir um padrão que seria esperado na ausência de um mecanismo ecológico específico (Gotelli and Graves 1996). Contudo, ressaltamos que os modelos nulos podem revelar padrões não comuns, mas eles não podem determinar os mecanismos responsáveis por gerar estes padrões (Gotelli and Graves 1996).
Os modelos nulos empregados para contrapor os padrões observados pelas métricas de diversidade filogenética utilizam a aleatorização dos dados de duas formas principais: i) aleatorizando o nome das espécies na árvore filogenética mantendo a estrutura e composição da matriz de co-ocorrência das espécies e o comprimento dos ramos da árvore inalterados; e ii) aleatorizando as linhas e/ou colunas da matriz de co-ocorrência das espécies (Gotelli 2000; Ulrich and Gotelli 2010). De forma geral, nas análises de diversidade filogenética as aleatorizações são repetidas 999 vezes (pode ser mais ou menos, a critério do pesquisador) e calcula-se a média e o desvio padrão dos valores gerados pelos modelos. Com estes dados, calcula-se o tamanho do efeito padronizado (do inglês Standardized Effect Size - SES) utilizando a seguinte fórmula:
- SES = (valor observado - média dos valores gerados na aleatorização)/ desvio padrão dos valores gerados na aleatorização
Os valores de SES são utilizados para rejeitar ou não a hipótese nula de que o padrão observado difere do esperado ao acaso. Contudo, tenha em mente que a definição do esquema de aleatorização dos modelos nulos não é meramente uma questão técnica (Götzenberger et al. 2012). A definição do esquema de aleatorização irá determinar quais os mecanismos ecológicos são permitidos ou excluídos no modelo nulo (Götzenberger et al. 2012). Consequentemente, ele estará avaliando diferentes hipóteses nulas.
Abaixo, demonstramos os códigos no R para calcular os modelos nulos para as métricas de diversidade filogenética.
Nearest Relative Index (NRI) ou Standardized Effect Size of MPD
Esta métrica calcula o tamanho do efeito padronizado para a métrica MPD. Contudo, NRI é calculado multiplicando os resultados do SES por -1. Valores positivos de NRI indicam agrupamento filogenético e valores negativos de NRI indicam dispersão filogenética (Webb, Ackerly, and Kembel 2008).
Veja a ajuda desta função usando ?ses.mpd() para ver todas as possibilidades de modelos nulos disponíveis.
## NRI ou SES_MPD
resultados_SES_MPD <- ses.mpd(composicao_especies_P, cophenetic(filogenia_aves),
null.model = "taxa.labels",
abundance.weighted = FALSE,
runs = 999)
# Mostra a riqueza de espéices, MPD observado, média e desvio padrão dos
# valores de MPD das aleatorizações, SES e o valor de p.
head(resultados_SES_MPD)
#> ntaxa mpd.obs mpd.rand.mean mpd.rand.sd mpd.obs.rank mpd.obs.z mpd.obs.p runs
#> Com_1 27 150.7914 153.9953 3.891718 215 -0.8232597 0.215 999
#> Com_2 26 157.3158 153.5833 4.367399 770 0.8546215 0.770 999
#> Com_3 25 146.1622 153.9931 4.476428 52 -1.7493791 0.052 999
#> Com_4 25 154.5005 153.5113 4.720348 551 0.2095591 0.551 999
#> Com_5 22 143.0727 153.7490 5.294432 24 -2.0165115 0.024 999
#> Com_6 18 141.1926 153.9709 6.951990 34 -1.8380846 0.034 999Somente as comunidades 5 e 6 apresentaram valores de p < 0.05 indicando que os resultados observados de MPD são menores que o esperado ao acaso (i.e., valores simulados). Neste caso, a composição de espécies presentes nessas duas comunidades apresenta agrupamento filogenético. Por outro lado, os valores de MPD observados para as outras comunidades são similares aos valores obtidos para comunidades simuladas com a redistribuição dos nomes das espécies na filogenia.
Nearest Taxon Index (NTI) ou Standardized Effect Size of MNTD
Esta métrica calcula o tamanho do efeito padronizado para a métrica MNTD. Contudo, NTI é calculado multiplicando os resultados do SES por -1. Valores positivos de NTI indicam agrupamento filogenético e valores negativos de NTI indicam dispersão filogenética (Webb, Ackerly, and Kembel 2008).
## NTI ou SES_MNTD
resultados_SES_MNTD <- ses.mntd(composicao_especies_P, cophenetic(filogenia_aves),
null.model = "taxa.labels",
abundance.weighted = FALSE,
runs = 999)
# Mostra a riqueza de espéices,MNTD observado, média e desvio padrão dos
# valores de MNTD das aleatorizações, SES e o valor de p.
head(resultados_SES_MNTD)
#> ntaxa mntd.obs mntd.rand.mean mntd.rand.sd mntd.obs.rank mntd.obs.z mntd.obs.p runs
#> Com_1 27 63.89727 63.30504 6.864478 518 0.08627467 0.518 999
#> Com_2 26 66.15828 64.81499 7.217753 575 0.18610860 0.575 999
#> Com_3 25 72.96912 65.76333 7.754651 811 0.92922217 0.811 999
#> Com_4 25 67.67170 65.70886 7.752673 600 0.25318258 0.600 999
#> Com_5 22 64.93477 69.46545 9.133114 305 -0.49607138 0.305 999
#> Com_6 18 63.72337 76.12099 11.819687 162 -1.04889562 0.162 999Somente a comunidade 9 apresentou valor de p < 0.05 indicando que o resultado observado de MNTD foi menor que o esperado ao acaso (i.e., valores simulados). Neste caso, a composição de espécies presente nessa comunidade apresenta agrupamento filogenético. Por outro lado, os valores de MNTD observados para as outras comunidades são similares aos valores obtidos para comunidades simuladas com a redistribuição dos nomes das espécies na filogenia.
Standardized Effect Size of PD
Esta métrica calcula o tamanho do efeito padronizado para a métrica PD (Webb, Ackerly, and Kembel 2008).
## SES_PD
resultados_SES_PD <- ses.pd(composicao_especies_P, filogenia_aves,
null.model = "independentswap",
runs = 999)
# Mostra a riqueza de espéices,MNTD observado, média e desvio padrão dos
# valores de PD das aleatorizações, SES e o valor de p.
head(resultados_SES_PD)
#> ntaxa pd.obs pd.rand.mean pd.rand.sd pd.obs.rank pd.obs.z pd.obs.p runs
#> Com_1 27 1259.315 1272.480 66.74674 429 -0.1972372 0.429 999
#> Com_2 26 1293.152 1238.690 68.04238 799 0.8004172 0.799 999
#> Com_3 25 1222.310 1201.471 65.51971 624 0.3180526 0.624 999
#> Com_4 25 1254.541 1205.879 68.34858 750 0.7119674 0.750 999
#> Com_5 22 1021.967 1096.024 67.73466 129 -1.0933409 0.129 999
#> Com_6 18 856.781 950.239 64.54864 76 -1.4478696 0.076 999Nenhuma comunidade apresentou valor de p < 0.05. Neste caso, os valores observados de PD são similares aos valores obtidos para comunidades simuladas com a redistribuição dos nomes das espécies na filogenia.
Standardized effect size do Phylosor
Não há pacotes que calculam o SES para a métrica Phylosor. Assim, iremos usar a função phylosor.rnd() para criar modelos nulos para o Physolor, e em seguida, iremos usar uma função criada por Pedro Braga & Katherine Hébert (disponível em https://pedrohbraga.github.io/CommunityPhylogenetics-Workshop/CommunityPhylogenetics-Workshop.html) para calcular os valores de SES e os valores de P.
## Standardized effect size do Phylosor
# Modelo nulo que rearranja o nome das espécies na filogenia.
modelos_nulo <- phylosor.rnd(composicao_especies_P, filogenia_aves,
null.model = "taxa.labels", runs = 9)
# Função para calcular o SES eo valor de P.
ses.physo <- function(obs, nulo_phylosor){
nulo_phylosor <- t(as.data.frame(lapply
(nulo_phylosor, as.vector)))
physo.obs <- as.numeric(obs)
physo.mean <- apply(nulo_phylosor, MARGIN = 2,
FUN = mean, na.rm = TRUE)
physo.sd <- apply(nulo_phylosor, MARGIN = 2,
FUN = sd, na.rm = TRUE)
physo.ses <- (physo.obs - physo.mean)/physo.sd
physo.obs.rank <- apply(X = rbind(physo.obs,
nulo_phylosor), MARGIN = 2,
FUN = rank)[1, ]
physo.obs.rank <- ifelse(is.na(physo.mean), NA,
physo.obs.rank)
data.frame(physo.obs, physo.mean, physo.sd,
physo.obs.rank, physo.ses,
physo.obs.p = physo.obs.rank/
(dim(nulo_phylosor)[1] + 1))
}
## Resultados
resultados <- ses.physo (resultados_Phylosor, modelos_nulo)
head(resultados)
#> physo.obs physo.mean physo.sd physo.obs.rank physo.ses physo.obs.p
#> 1 0.7856828 0.7915561 0.04011508 6 -0.1464099 0.6
#> 2 0.8052839 0.8813422 0.03356047 1 -2.2663056 0.1
#> 3 0.7831520 0.8174306 0.04545519 2 -0.7541175 0.2
#> 4 0.8586780 0.8687616 0.03659588 5 -0.2755416 0.5
#> 5 0.6717414 0.7460991 0.02806215 1 -2.6497526 0.1
#> 6 0.7414284 0.6904007 0.04842748 9 1.0536941 0.9Nenhum valor de similaridade entre pares comunidade apresentou valor de p < 0.05. Neste caso, os valores de Phylosor observados são similares aos valores obtidos para as comunidades simuladas com a redistribuição dos nomes das espécies na filogenia.
13.6 Para se aprofundar
13.6.1 Livros
- Recomendamos aos interessados(as) os livros: i) Swenson (2014) Functional and Phylogenetic Ecology in R; ii) Paradis (2012) Analysis of Phylogenetics and Evolution in R; iii) Cadotte & Davies (2016) Phylogenies in Ecology, iv) Gotelli & Graves (1996) Null Models in Ecology; e v) Magurran & McGill (2011) Biological Diversity Frontiers in Measurement and Assessment.
13.6.2 Links
O blog Ferramentas filogenéticas para biologia comparada do pesquisador Liam Revell é uma ferramenta excelente para obter informações e aplicações das análises filogenéticas diretamente no R.
13.7 Exercícios
13.1
Carregue os dados - anuros_composicao (i.e., 211 espécies de anuros coletados em 44 localidades na Mata Atlântica), anuros_ambientais (i.e., variáveis climáticas, topográficas e coordenadas geográficas) e filogenia_anuros (filogenia das 211 espécies) - que estão no pacote ecodados. Use a função varpart() do pacote vegan para testar a importância relativa dos efeitos da precipitação anual, range altitudinal e temperatura anual na distribuição espacial da diversidade filogenética (PD) e Endemismo filogenético (PE). Calcule o SES para verificar se os resultados da diversidade filogenética (PD) diferem do esperado ao acaso devido ao número de espécies em cada comunidade. Qual a sua interpretação sobre os resultados?
13.2
Carregue os dados - anuros_composicao (i.e., 211 espécies de anuros coletados em 44 localidades na Mata Atlântica), anuros_ambientais (i.e., variáveis climáticas, topográficas e coordenadas geográficas) e filogenia_anuros (filogenia das 211 espécies) - que estão no pacote ecodados. Use a função varpart() do pacote vegan para testar a importância relativa dos efeitos da precipitação anual, range altitudinal e temperatura anual na distribuição espacial do NRI e NTI. Qual a sua interpretação sobre os resultados?
13.3
Carregue os dados - anuros_composicao (i.e., 211 espécies de anuros coletados em 44 localidades na Mata Atlântica), anuros_ambientais (i.e., variáveis climáticas, topográficas e coordenadas geográficas) e filogenia_anuros (filogenia das 211 espécies) - que estão no pacote ecodados. Use a função varpart() do pacote vegan para testar a importância relativa dos efeitos da precipitação anual, range altitudinal e distância geográfica na distribuição espacial dos diferentes componentes da diversidade beta filogenética (Phylosor). Qual a sua interpretação sobre os resultados?